Circles
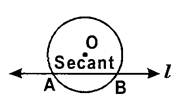
- Secant: A line which intersects a circle at two distinct points is called a secant of a circle.
- Tangent: A line touching a circle at exactly one point only is called a tangent to the circle at that point.
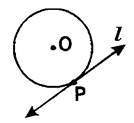
- Point of contact: The point P at which the tangent touches the circle is called the point of contact.
- Number of tangents to a circle:
|
Position of the point w.r.t. the circle
|
Number of tangents
|
|
Inside
|
0
|
|
On
|
1
|
|
Outside
|
2
|
- Length of a tangent: The length of the line segment of the tangent between a given point and the given point of contact with the circle is called the length of the tangent from the point to the circle.
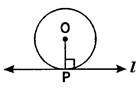
The tangent at any point of a circle is perpendicular to the radius through the point of contact. In other words, the angle between a tangent and the radius through the point of contact is\[{{90}^{o}}\].
- The lengths of tangents drawn from an external point to a circle are equal.
If AP and AQ are two tangents from an external point A to the circle, then AP = AQ.
- Two tangents drawn from an external point subtend equal angles at the centre and are equally inclined to the line segment joining the centre to that point.
- The tangents drawn at the ends of a diameter of a circle are parallel.
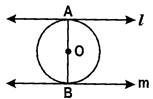
- The line segments joining the point of contact of two parallel tangents to a circle is a diameter of the circle.
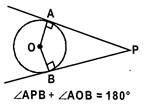
- The angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segments joining the points of contact to the centre.
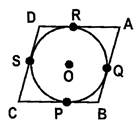
- There is one and only one tangent at any point on the circumference of a circle.
- A parallelogram circumscribing a circle is a rhombus.
- The opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
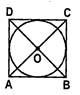
\[\angle AOB+\angle COD={{180}^{o}}\]
\[\angle BOC+\angle AOD={{180}^{o}}\]
- In two concentric circles, the chord of the larger circle which touches the smaller circle is bisected at the point of contact.
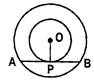
\[\text{AP}=\text{PB}\]
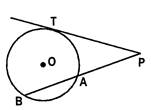
- If PAB is a secant to a circle intersecting it at A and B and PT is a tangent, then\[\text{PA}\times \text{PB}=\text{P}{{\text{T}}^{\text{2}}}\].