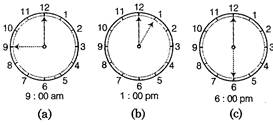
Answer:
(a) Number of divisions between 9 to 12 = 3 We know that, 12 divisions \[={{360}^{o}}\] 1 division \[=\frac{{{360}^{o}}}{12}\] \[\therefore \] 3 divisions \[=\frac{{{360}^{o}}}{12}\times 3={{90}^{o}}\] (b) Number of divisions between 12 to 1 = 1 We know that, 12 divisions \[={{360}^{o}}\] \[\therefore \] 1 division\[=\frac{{{360}^{o}}}{12}={{30}^{o}}\] (c) Now, number of divisions between 12 to 6 = 6 We know that, 12 divisions \[={{360}^{o}}\] \[\therefore \] 1 division \[=\frac{{{360}^{o}}}{12}\] \[\therefore \] 6 divisions \[=\frac{{{360}^{o}}}{12}\times 6={{180}^{o}}\] Hence, angle between the hands of the clock in each figure is \[{{90}^{o}},\,\,{{30}^{o}}\] and \[{{180}^{o}}\], respectively. Alternate Solution Here, we will use the protractor to find measure of required angle. Firstly, place the protractor so that the mid-point of its straight edge lies on the centre of clock (i.e. vertex of angle) and greater hand of the clock (i.e. on side of angle) along the straight edge of the protractor, then mark shown by smaller hand of the clock (i.e. second side of angle) on the curved edge gives the degree measure of angle formed at 9 : 00 am. Thus, at 9 : 00 am, angle measure is \[{{90}^{o}}\]. Similarly, angle measure between the hands of the clock at 1 : 00 pm is 30° and at 6 : 00 pm is \[{{180}^{o}}\].
You need to login to perform this action.
You will be redirected in
3 sec
