question_answer 1)

                Find the rule which gives the number of matchsticks required to make the following matchstick patterns. Use a variable to write the rule. (a) A pattern of letter T as T (b) A pattern of letter Z as Z (c)A pattern of letter U as U (d) A pattern of letter V as V (e) A pattern of letter E as E (f) A pattern of letter S as S (g) A pattern of letter A as A TIPS Firstly, form the given letter by matchsticks and then form the pattern. Since, number of letter is increasing in this pattern, so let the number of letter is a variable. Put the different values 1, 2, 3, ... n, of variable, find number of matchsticks and then get the required rule.                

Answer:

                (a) One T can be formed by 2 matchsticks and 2T can be formed by 4 matchsticks. Thus, we get the following patterns of letter T. Here, the number of Ts is increasing. So, let variable n denotes the number of Ts. Now, number of matchsticks required to make pattern of T are given below:         For \[n=1,\]the number of matchsticks required \[=2\times 1=2\] For \[n=2,\]the number of matchsticks required \[=2\times 2=4\] For \[n=3,\] the number of matchsticks required \[=2\times 3=6\] For \[n=n\], the number of matchsticks required \[=2\times n=2re\] Hence, the required rule for a pattern of letter T is \[2n\]. (b) One Z can be formed by 3 matchsticks and 2Z can be formed by 6 matchsticks. Thus, we get the following patterns of letter Z. Here, the number of Zs is increasing. So, let variable re denotes the number of Zs. Now, the number of matchsticks required to make pattern of 'Z' are given below: For \[n=1,\] the number of matchsticks required \[=3\times 1=3\] For \[n=2,\] the number of matchsticks required \[=3\times 2=6\] For \[n=3,\] the number of matchsticks required \[=3\times 3=9\] For \[n=n,\] the number of matchsticks required \[=3\times n=3n\] Hence, the required rule for a pattern of letter Z is 3re. (c) One U can be formed by 3 matchsticks and 2U can be formed by 6 matchsticks. Thus, we get the following pattern of letter U. Here, the number of Us is increasing. Let variable re denotes the number of Us. Now, the number of matchsticks required to make pattern of 'U' are given below: For \[n=1,\] the number of matchsticks required \[=3\times 1=3\] For \[n=2,\] the number of matchsticks required \[=3\times 2=6\] For \[n=3,\] the number of matchsticks required \[=3\times 3=9\] For \[n=n,\] the number of matchsticks required \[=3\times n=3n\] Hence, the required rule for a pattern of letter U is 3re. (d) One V can be formed by 2 matchsticks and 2V can be formed by 4 matchsticks. Thus, we get the following pattern of letter V. Here, the number of Vs is increasing. Let variable \[n\]  denotes the number of Vs. Now, the number of matchsticks required to make pattern of ?V? are given below: For \[n=1,\] the number of matchsticks required \[=2\times 1=2\] For \[n=2,\]the number of matchsticks required \[=2\times 2=4\] For \[n=3,\]the number of matchsticks required  \[=2\times 3=6\] For \[n=n,\] the number of matchsticks required \[=2\times n=2n\] Hence, the required rule for a pattern of letter V is \[2n\]. (e) One E can be formed by 5 matchsticks and 2E can be formed by 10 matchsticks. Thus, we get the following pattern of letter E. 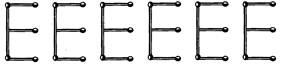Let variable re denotes the number of Es. Now, the number of matchsticks required to make pattern of ?E? are given below: For \[n=1,\] the number of matchsticks required \[=5\times 1=5\] For \[n=2,\] the number of matchsticks required \[=5\times 2=10\] For \[n=3,\] the number of matchsticks required \[=5\times 3=15\] For \[n=n,\] the number of matchsticks required \[=5\times n=5n\]. Hence, the required rule for a pattern of letter E is 5re. (f) One S can be formed by 5 matchsticks and 2S can be formed by 10 matchsticks. Thus, we get the following pattern of letter S. 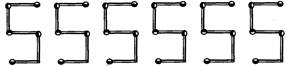Let variable n denotes the number of Ss. Now, number of matchsticks required to make pattern ?S? is For \[n=1,\] number of matchsticks \[=5\times 1=5\] For \[n=2,\] number of matchsticks \[=5\times 2=10\] For \[n=3,\] number of matchsticks \[=5\times 3=15\] For \[n=n,\]number of matchsticks  \[=5\times n=5n\] Thus, the required rule for a pattern of letter S is 5re. (g) One A can be formed by 6 matchsticks and 2A can be formed by 12 matchsticks. Thus, we get the following pattern of letter A. 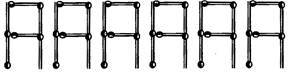Here, the number 'of As is increasing. Let variable n denotes the number of As. Now, the number of matchsticks required to make pattern 'A' is For \[n=1,\] the number of matchsticks required \[=6\times 1=6\] For \[n=2,\] the number of matchsticks required \[=6\times 2=12\] For \[n=3,\]the number of matchsticks required \[=6\times 3=18\] For \[n=n,\] the number of matchsticks required \[=6\times n=6n\] Hence, the required rule for a pattern of letter ?A? is \[6n\].