question_answer 12)

One kind of cake requires 200 g of flour and 25g of fat, and another kind of cake requires 100g of flour and 50 g of fat. Find the maximum number of cakes which can be made from 5 kg of flour and 1 kg of fat assuming that there is no shortage of the other ingredients, used in making the cakes. 

Answer:

Let number of cakes of first kind = x       and the number of cakes of second kind = y       The contents of cake are given below

Cake	Flour	Fat
First kind	200	25
Second Kind	100	50
Quantity available	5 kg	1 kg

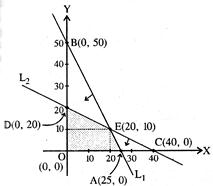
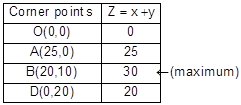
      Therefore the above L.P.P. is given as maximize,       Z = x + y, subject to the constraints.             200 x + 100 y       and 25x + 50 y       i..e.             2x + y       and x + 2y       L1: 2x + y = 50                     L2 : x + 2y = 40                                               Here Z is maximum at E(20, 10)        Number of cake of first kind x =20       Number of cakes of second kind, y = 10        Maximum number of cakes = 20 +10 = 30.