Answer:
Consider ![]() Since
modulus function is everywhere continuous and sum of two continuous function is
also continuous.
Differentiability
of f(x)
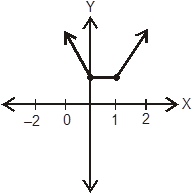
Graph
of f(x) shows, that f(x) is every where derivable except possible at x = 0 and
x = 1
Since
modulus function is everywhere continuous and sum of two continuous function is
also continuous.
Differentiability
of f(x)
Graph
of f(x) shows, that f(x) is every where derivable except possible at x = 0 and
x = 1
 At x = 0
L.H.D. =
At x = 0
L.H.D. = ![]()
![]()
![]()
![]() R.H.D.
R.H.D. ![]()
![]()
![]()
![]() Since L.H.D.
Since L.H.D. ![]() R.H.D.
f(x) is not
derivable at x = 0.
At x = 1
L.H.D. =
R.H.D.
f(x) is not
derivable at x = 0.
At x = 1
L.H.D. = ![]()
![]()
![]()
![]() R.H.D.
R.H.D. ![]()
![]()
![]()
![]()
![]() Since L.H.D.
Since L.H.D. ![]()
![]() is not
derivable at x = 1 also.
Hence f(x) is
continuous everywhere but not derivable at exactly two points. Hence the result.
is not
derivable at x = 1 also.
Hence f(x) is
continuous everywhere but not derivable at exactly two points. Hence the result.
You need to login to perform this action.
You will be redirected in
3 sec
