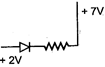
question_answer 1) In beta minus decay a neutron transforms with the nucleus according to.
A)
\[p\to n+{{e}^{+}}+v\]
done
clear
B)
\[n\to p+{{e}^{-}}+\bar{v}\]
done
clear
C)
\[n\to p+{{e}^{+}}+\bar{v}\]
done
clear
D)
\[n\to p+{{e}^{+}}+v\]
done
clear
View Answer play_arrow
question_answer 2) The element with maximum value of binding energy per nucleon is
A)
iron
done
clear
B)
aluminium
done
clear
C)
uranium
done
clear
D)
hydrogen
done
clear
View Answer play_arrow
question_answer 3) If the particles listed below all have the same kinetic energy, which one would possess the shortest de-Broglie wavelength?
A)
Deuteron
done
clear
B)
\[\alpha \]-particle
done
clear
C)
Proton
done
clear
D)
Electron
done
clear
View Answer play_arrow
question_answer 4) Which of the following quantities for a nucleus is independent of its mass number?
A)
Density
done
clear
B)
Volume
done
clear
C)
Mass
done
clear
D)
Radius
done
clear
View Answer play_arrow
question_answer 5) The SI unit of activity of a radioactive sample is
A)
Curie
done
clear
B)
Rutherford
done
clear
C)
Becquerel
done
clear
D)
Mill curie
done
clear
View Answer play_arrow
question_answer 6) P-type semiconductor is obtained by doping
A)
germanium with arsenic
done
clear
B)
germanium with aluminium
done
clear
C)
germanium with antimony
done
clear
D)
germanium with phosphorus
done
clear
View Answer play_arrow
question_answer 7) A cubical block rests on an inclined plane of coefficient of friction \[\mu =1/\sqrt{3}\]. What should be the angle of inclination so that the block Just slides down the inclined plane?
A)
\[{{30}^{o}}\]
done
clear
B)
\[{{60}^{o}}\]
done
clear
C)
\[{{45}^{o}}\]
done
clear
D)
\[{{90}^{o}}\]
done
clear
View Answer play_arrow
question_answer 8) The acceleration of an object moving in a circle of radius R with uniform speed v is
A)
\[\frac{{{v}^{2}}}{R}\]
done
clear
B)
\[\frac{{{v}^{2}}}{2R}\]
done
clear
C)
\[\frac{2{{v}^{2}}}{R}\]
done
clear
D)
\[\frac{3{{v}^{2}}}{2R}\]
done
clear
View Answer play_arrow
question_answer 9) If a projectile is launched with velocity \[{{v}_{0}},\] making an angle \[\theta \] with x-axis, then its time of flight T is
A)
\[T=\frac{v_{0}^{2}\sin 2\theta }{g}\]
done
clear
B)
\[T=\frac{v_{0}^{2}\,\,{{\sin }^{2}}\theta }{2g}\]
done
clear
C)
\[T=\frac{v_{0}^{2}}{g}\]
done
clear
D)
\[T=\frac{2{{v}_{0}}\,\sin \,\theta }{g}\]
done
clear
View Answer play_arrow
question_answer 10) A batsman hits back a ball straight in the direction of the bowler without changing its initial speed of\[12\text{ }m/s\]. If the mass of the ball is \[0.15\text{ }kg\]the impulse imparted to the ball is
A)
\[36\text{ }Ns\]
done
clear
B)
\[3.6\text{ }Ns\]
done
clear
C)
\[0.36\text{ }Ns\]
done
clear
D)
\[0.036\text{ }Ns\]
done
clear
View Answer play_arrow
question_answer 11) Which of the following statements' is correct regarding the photoelectric experiment?
A)
The photocurrent increases with intensity of light
done
clear
B)
Stopping potential increases with increase in intensity of incident light
done
clear
C)
The photo current increases with increase in frequency
done
clear
D)
All of the above
done
clear
View Answer play_arrow
question_answer 12) In a double-slit experiment, the two slits are separated by \[1\text{ }mm\]and the screen is placed \[1\text{ }m\]away. The fringe separation for blue green light of wavelength \[500\text{ }nm\]is
A)
\[10\text{ }mm\]
done
clear
B)
\[0.5\text{ }mm\]
done
clear
C)
\[20\,\,mm\]
done
clear
D)
\[15\,\,mm\]
done
clear
View Answer play_arrow
question_answer 13) Rainbow is a phenomenon due to
A)
dispersion alone
done
clear
B)
refraction alone
done
clear
C)
reflection alone
done
clear
D)
combined effect of dispersion, refraction and reflection
done
clear
View Answer play_arrow
question_answer 14) In the case of light waves from two coherent\[{{S}_{1}}\] and \[{{S}_{2}}\] there will be constructive interference at an arbitrary point p, if the path difference \[{{S}_{1}}P-{{S}_{2}}P\] is
A)
\[\left( n+\frac{1}{2} \right)\lambda \]
done
clear
B)
\[n\lambda \]
done
clear
C)
\[\left( n-\frac{1}{2} \right)\lambda \]
done
clear
D)
\[\frac{\lambda }{2}\]
done
clear
View Answer play_arrow
question_answer 15) The de-Broglie wavelength \[\lambda \]of an electron accelerated through a potential V(in volt) is
A)
\[\frac{1.227}{\sqrt{V}}nm\]
done
clear
B)
\[\frac{0.1227}{\sqrt{V}}nm\]
done
clear
C)
\[\frac{0.01227}{\sqrt{V}}nm\]
done
clear
D)
\[\frac{0.1227}{\sqrt{V}}\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
View Answer play_arrow
question_answer 16) A gardener pushes a lawn roller through a distance\[20\text{ }m\]. If he applies a force of \[20kg-wt\] in a direction inclined at \[60{}^\circ \] to the ground, the work done by him is
A)
\[1960\text{ }J\]
done
clear
B)
\[196\text{ }J\]
done
clear
C)
\[1.96\text{ }J\]
done
clear
D)
\[196\text{ }kJ\]
done
clear
View Answer play_arrow
question_answer 17) If two bodies stick together after collision and move as a single body, the collision is said to be
A)
perfectly inelastic
done
clear
B)
elastic
done
clear
C)
inelastic
done
clear
D)
perfectly elastic
done
clear
View Answer play_arrow
question_answer 18) If \[{{\mu }_{s}}\] is coefficient of static friction, the maximum speed \[{{v}_{\max }}\]with which a vehicle can negotiate an unbanked curved track having radius R and inclined at an angle \[\theta \] with respect to horizontal plane is
A)
\[{{v}_{\max }}=\sqrt{Rg\,\,\tan \theta }\]
done
clear
B)
\[{{v}_{\max }}=\sqrt{{{\mu }_{s}}\,\,Rg}\]
done
clear
C)
\[\sqrt{Rg}\]
done
clear
D)
\[\sqrt{\tan \theta /Rg}\]
done
clear
View Answer play_arrow
question_answer 19) For a moving particle (mass m, velocity v) having a momentum p, which one of the following correctly describes the kinetic energy of the particle?
A)
\[\frac{{{p}^{2}}}{2m}\]
done
clear
B)
\[\frac{p}{2m}\]
done
clear
C)
\[\frac{{{v}^{2}}}{2m}\]
done
clear
D)
\[\frac{v}{2m}\]
done
clear
View Answer play_arrow
question_answer 20) SI unit of power is
A)
joule
done
clear
B)
erg
done
clear
C)
newton
done
clear
D)
watt
done
clear
View Answer play_arrow
question_answer 21) Sun is visible a little before the actual sunrise and until a little after the actual sunset. This is due to
A)
total internal reflection
done
clear
B)
reflection
done
clear
C)
refraction
done
clear
D)
polarization
done
clear
View Answer play_arrow
question_answer 22) The part of the spectrum of the electro- magnetic radiation used to cook food is
A)
Ultraviolet rays
done
clear
B)
Cosmic rays
done
clear
C)
X-rays
done
clear
D)
Microwaves
done
clear
View Answer play_arrow
question_answer 23) An LCR series circuit is under resonance. \[{{I}_{m}}\] is current amplitude, \[{{V}_{m}}\] is voltage amplitude, R is the resistance, Z is the impedance, \[{{X}_{L}}\] is the inductive reactance and \[{{X}_{C}}\] is the capacitive reactance then,
A)
\[{{I}_{m}}=\frac{{{V}_{m}}}{Z}\]
done
clear
B)
\[{{I}_{m}}=\frac{{{V}_{m}}}{{{X}_{L}}}\]
done
clear
C)
\[{{I}_{m}}=\frac{{{V}_{m}}}{{{X}_{C}}}\]
done
clear
D)
\[{{I}_{m}}=\frac{{{V}_{m}}}{R}\]
done
clear
View Answer play_arrow
question_answer 24) A point source that emits waves uniformly in all directions, produces wave fronts that are
A)
spherical
done
clear
B)
elliptical
done
clear
C)
cylindrical
done
clear
D)
planar
done
clear
View Answer play_arrow
question_answer 25) In the case of an inductor
A)
voltage lags the current by \[\pi /2\]
done
clear
B)
voltage leads the current by \[\pi /2\]
done
clear
C)
voltage leads the current by \[\pi /3\]
done
clear
D)
voltage leads the current by \[\pi /4\]
done
clear
View Answer play_arrow
question_answer 26) For a stretched string of length L fixed at both ends, the frequency of the fundamental mode of vibration is (v is the velocity if travelling waves in the string)
A)
\[\frac{v}{2L}\]
done
clear
B)
\[\frac{v}{L}\]
done
clear
C)
\[\frac{v}{4L}\]
done
clear
D)
\[\frac{v}{3L}\]
done
clear
View Answer play_arrow
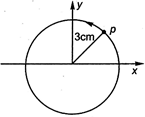
question_answer 27)
The figure shows circular motion of a reference particle to represent simple harmonic motion. The amplitude of simple harmonic motion is
A)
\[2\text{ }cm\]
done
clear
B)
\[3\text{ }cm\]
done
clear
C)
\[\text{4 }cm\]
done
clear
D)
\[3\,m\]
done
clear
View Answer play_arrow
question_answer 28) In the case of a travelling wave, the reflection at a rigid boundary will take place with a phase change of
A)
\[\frac{\pi }{2}\,rad\]
done
clear
B)
\[\frac{\pi }{4}\,rad\]
done
clear
C)
\[\pi \,\,rad\]
done
clear
D)
\[\frac{\pi }{6}\,\,rad\]
done
clear
View Answer play_arrow
question_answer 29) If \[{{u}_{1}}\] and \[{{u}_{2}}\] are the frequencies of two tuning forks then the beat frequency is
A)
\[\frac{{{u}_{1}}}{{{u}_{2}}}\]
done
clear
B)
\[{{u}_{1}}+{{u}_{2}}\]
done
clear
C)
\[\frac{{{u}_{2}}}{{{u}_{1}}}\]
done
clear
D)
\[{{u}_{1}}-{{u}_{2}}\]
done
clear
View Answer play_arrow
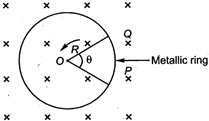
question_answer 30)
A metallic rod of length R is rotated with an angular frequency co with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius R, about an axis passing through the centre and perpendicular to the plane of the ring. There is a magnetic field B, perpendicular to the plane of the ring. The emf induced between the centre and the metallic ring is
A)
\[B\,\,\sin \,\,\omega t\]
done
clear
B)
\[\frac{B{{R}^{2}}\omega }{2}\]
done
clear
C)
\[2\,B{{R}^{2}}\omega \]
done
clear
D)
\[B{{R}^{2}}\omega \]
done
clear
View Answer play_arrow
question_answer 31) The statement "Polarity of induced emf is such that it tends to produce a current which opposes the change in magnetic flux that produced it" is known as
A)
Faraday's law
done
clear
B)
Gauss's law
done
clear
C)
Coulomb's law
done
clear
D)
Lenz's law
done
clear
View Answer play_arrow
question_answer 32) When the current changes form \[+2A\]to \[-3A\] in \[0.05,\]an emf of \[8\text{ }V\]is induced in a coil. The coefficient of self inductance of the coil is
A)
\[0.2\text{ }H\]
done
clear
B)
\[0.4\text{ }H\]
done
clear
C)
\[0.8\text{ }H\]
done
clear
D)
\[0.1\text{ }H\]
done
clear
View Answer play_arrow
question_answer 33) A car moving with a speed of \[50\text{ }km/h\]can be stopped by brakes, over a distance of \[6m\]. If the same car is moving at a speed of \[100\text{ }km/h,\] the stopping distance is
A)
\[12\text{ }m\]
done
clear
B)
\[18\text{ }m\]
done
clear
C)
\[6\text{ }m\]
done
clear
D)
\[24\text{ }m\]
done
clear
View Answer play_arrow
question_answer 34) The dimensions of impulse are
A)
\[[ML{{T}^{-1}}]\]
done
clear
B)
\[[M{{L}^{2}}{{T}^{-1}}]\]
done
clear
C)
\[[M{{L}^{-1}}{{T}^{-1}}]\]
done
clear
D)
\[[M{{T}^{-1}}]\]
done
clear
View Answer play_arrow
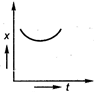
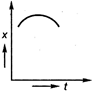
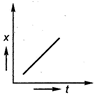
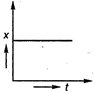
question_answer 35) Position-time graph for motion with zero acceleration is
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Answer play_arrow
question_answer 36) If the magnetic susceptibility of a material is large and positive. The material is
A)
diamagnetic
done
clear
B)
ferromagnetic
done
clear
C)
paramagnetic
done
clear
D)
perfect diamagnetic
done
clear
View Answer play_arrow
question_answer 37) A 100 turn closely wound circular coil of radius \[10\text{ }cm\]carries a current of \[3.2\text{ }A\]. The magnetic moment of the coil is, approximately
A)
\[5\text{ }A{{m}^{2}}\]
done
clear
B)
\[10\text{ }A{{m}^{2}}\]
done
clear
C)
\[20\text{ }A{{m}^{2}}\]
done
clear
D)
\[40\text{ }A{{m}^{2}}\]
done
clear
View Answer play_arrow
question_answer 38) The particle that cannot be accelerated by a cyclotron is
A)
proton
done
clear
B)
\[\alpha \]-particle
done
clear
C)
electron
done
clear
D)
deuteron nucleus
done
clear
View Answer play_arrow
question_answer 39) The material whose resistivity is insensitive to temperature is
A)
silicon
done
clear
B)
copper
done
clear
C)
silver
done
clear
D)
nichrome
done
clear
View Answer play_arrow
question_answer 40) The path of a charged particle in a uniform magnetic field, when the velocity and the magnetic field are perpendicular to each other is a
A)
circle
done
clear
B)
parabola
done
clear
C)
helix
done
clear
D)
straight line
done
clear
View Answer play_arrow
question_answer 41) A galvanometer can be converted into a voltmeter by connecting
A)
low resistance in series
done
clear
B)
high resistance in series
done
clear
C)
low resistance in parallel
done
clear
D)
high resistance in parallel
done
clear
View Answer play_arrow
question_answer 42) The angle which the total magnetic field of earth makes with the surface of the earth is called
A)
declination
done
clear
B)
magnetic meridian .
done
clear
C)
geographic meridian
done
clear
D)
inclination
done
clear
View Answer play_arrow
question_answer 43) A constant torque of \[3.14\text{ }Nm\] is exerted on a pivoted wheel. If the angular acceleration of the wheel is \[4\pi \text{ }rad/{{s}^{2}},\] then the moment of Inertia of the wheel is
A)
\[0.25\text{ }kg-{{m}^{2}}\]
done
clear
B)
\[2.5\text{ }kg-{{m}^{2}}\]
done
clear
C)
\[4.5\text{ }kg-{{m}^{2}}\]
done
clear
D)
\[25\text{ }kg-{{m}^{2}}\]
done
clear
View Answer play_arrow
question_answer 44) The temperature of the sink of a Carnot engine is \[{{27}^{o}}C\]and its efficiency is 25%. The temperature of the source is
A)
\[{{227}^{o}}C\]
done
clear
B)
\[{{27}^{o}}C\]
done
clear
C)
\[{{327}^{o}}C\]
done
clear
D)
\[{{127}^{o}}C\]
done
clear
View Answer play_arrow
question_answer 45) A thermodynamic process in which the system is insulated from the surroundings and no heat flows between the system and the surroundings is an
A)
isothermal process
done
clear
B)
adiabatic process
done
clear
C)
isochoric process
done
clear
D)
isobaric process
done
clear
View Answer play_arrow
question_answer 46) The moment of inertia of rod of mass M length I about an axis perpendicular to it through one end is
A)
\[\frac{M{{l}^{2}}}{12}\]
done
clear
B)
\[\frac{M{{l}^{2}}}{2}\]
done
clear
C)
\[\frac{M{{l}^{2}}}{3}\]
done
clear
D)
\[\frac{M{{l}^{2}}}{4}\]
done
clear
View Answer play_arrow
question_answer 47) In the diagram shown below, \[{{m}_{1}}\] and \[{{m}_{2}}\] are the masses of two particles and \[{{x}_{1}}\] and \[{{x}_{2}}\] are the respective distances from the origin O. The centre of mass of the system is
A)
\[\frac{{{m}_{1}}{{x}_{2}}+{{m}_{2}}{{x}_{1}}}{{{m}_{1}}+{{m}_{2}}}\]
done
clear
B)
\[\frac{{{m}_{1}}+{{x}_{2}}}{2}\]
done
clear
C)
\[\frac{{{m}_{1}}{{x}_{1}}+{{m}_{2}}{{x}_{2}}}{{{m}_{1}}+{{m}_{2}}}\]
done
clear
D)
\[\frac{{{m}_{1}}{{m}_{2}}+{{x}_{1}}{{x}_{2}}}{{{m}_{1}}+{{m}_{2}}}\]
done
clear
View Answer play_arrow
question_answer 48) Fractional increase in resistivity per unit increase in temperature is defined as
A)
resistivity
done
clear
B)
temperature coefficient of resistivity
done
clear
C)
conductivity
done
clear
D)
drift velocity
done
clear
View Answer play_arrow
question_answer 49) Magnitude of drift velocity per unit electric field is
A)
current density
done
clear
B)
current
done
clear
C)
resistivity
done
clear
D)
mobility
done
clear
View Answer play_arrow
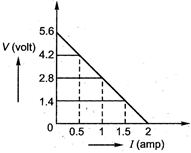
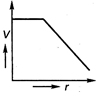
question_answer 50)
Four cells of identical emf E and internal resistance r are connected is series to a variable resistor. The following graph shows the variation of terminal voltage of the combination with current. The emf of each cell used is
A)
\[1.4\,\,V\]
done
clear
B)
\[5.6\,\,V\]
done
clear
C)
\[2\,\,V\]
done
clear
D)
\[1\,\,V\]
done
clear
View Answer play_arrow
question_answer 51) Kirchhoff?s 1st law for analysis of current at a junction in a circuit is based on
A)
conservation of charge
done
clear
B)
conservation of energy
done
clear
C)
conservation of momentum
done
clear
D)
Newton's 3rd law of motion
done
clear
View Answer play_arrow
question_answer 52) Water is used as a coolant in automobile radiators owing to its high
A)
viscosity
done
clear
B)
surface tension
done
clear
C)
latent heat
done
clear
D)
specific heat capacity
done
clear
View Answer play_arrow
question_answer 53) The SI unit of thermal conductivity is
A)
\[Js{{m}^{-1}}{{K}^{-1}}\]
done
clear
B)
\[{{W}^{-1}}{{m}^{-1}}{{K}^{-1}}\]
done
clear
C)
\[W{{m}^{-1}}{{K}^{-1}}\]
done
clear
D)
\[W{{m}^{-2}}{{K}^{-1}}\]
done
clear
View Answer play_arrow
question_answer 54) For a body immersed in a liquid, when the weight of the body is less than the up thrust then the body will
A)
float partially immersed
done
clear
B)
sink
done
clear
C)
float fully immersed
done
clear
D)
be of zero weight
done
clear
View Answer play_arrow
question_answer 55) If R is the radius of a soap bubble and S its surface tension, then the excess pressure inside is
A)
\[\frac{2S}{R}\]
done
clear
B)
\[\frac{3S}{R}\]
done
clear
C)
\[\frac{4S}{R}\]
done
clear
D)
\[\frac{S}{R}\]
done
clear
View Answer play_arrow
question_answer 56) An aeroplane of mass \[3\times {{10}^{4}}\,kg\] and total wing area of \[120\text{ }{{m}^{2}}\]is in a level flight at some height. The difference in pressure between the upper and lower surface of its wings in kpa is \[g=20m/{{s}^{2}}\])
A)
\[2.5\]
done
clear
B)
\[5\]
done
clear
C)
\[10\]
done
clear
D)
\[15\]
done
clear
View Answer play_arrow
question_answer 57) The rate of loss of heat of a body is directly proportional to the difference of temperature of the body and the surroundings. This statement is known as
A)
Stefan's law
done
clear
B)
Newton's law of cooling
done
clear
C)
Wien's law
done
clear
D)
Kirchhoff?s law
done
clear
View Answer play_arrow
question_answer 58) A parallel plate capacitor has two square plates with equal and opposite charges. The surface charge densities on the plates are \[+\sigma \] and \[-\sigma \] respectively. In the region between the plates the magnitude of the electric field is
A)
\[\frac{\sigma }{2{{\varepsilon }_{0}}}\]
done
clear
B)
\[\frac{\sigma }{{{\varepsilon }_{0}}}\]
done
clear
C)
zero
done
clear
D)
None of these
done
clear
View Answer play_arrow
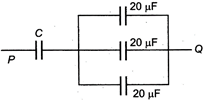
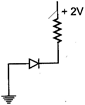
question_answer 59)
If the equivalent capacitance between P and Q of the combination of the capacitors shown in figure below is \[30\text{ }\mu \text{F}\], the capacitor C is
A)
\[60\,\mu F\]
done
clear
B)
\[30\,\mu F\]
done
clear
C)
\[10\,\mu F\]
done
clear
D)
\[5\,\mu F\]
done
clear
View Answer play_arrow
question_answer 60) A charge Q is placed at the origin. The electric potential due to this charge at a given point in space is V. The work done by an external force in bringing another charge q from infinity up to the point is
A)
\[\frac{V}{q}\]
done
clear
B)
\[Vq\]
done
clear
C)
\[V+q\]
done
clear
D)
\[V\]
done
clear
View Answer play_arrow
question_answer 61) A capacitor of capacitance \[{{C}_{1}}\] is charged to a potential V and then connected in parallel to an uncharged capacitor of capacitance \[{{C}_{2}}\].The final potential difference across each capacitor will be
A)
\[\frac{{{C}_{1}}V}{{{C}_{1}}+{{C}_{2}}}\]
done
clear
B)
\[\frac{{{C}_{2}}V}{{{C}_{1}}+{{C}_{2}}}\]
done
clear
C)
\[1+\frac{{{C}_{2}}}{{{C}_{1}}}\]
done
clear
D)
\[1-\frac{{{C}_{2}}}{{{C}_{1}}}\]
done
clear
View Answer play_arrow
question_answer 62) In the case of a sphere falling through a viscous medium, it attains terminal velocity when
A)
viscous force plus buoyant force becomes equal to force of gravity
done
clear
B)
viscous force is zero
done
clear
C)
viscous force plus force of gravity becomes equal to buoyant force
done
clear
D)
buoyant force become equal to force of gravity
done
clear
View Answer play_arrow
question_answer 63) A radio wave that travels in a straight line from the transmitting antenna to the receiving antenna is knows as
A)
sky wave
done
clear
B)
ground wave
done
clear
C)
space wave
done
clear
D)
ionosphere wave
done
clear
View Answer play_arrow
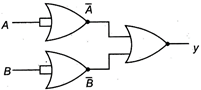
question_answer 64)
The output y of the circuit shown is
A)
\[y=A.B\]
done
clear
B)
\[y=\overline{A}.\overline{B}\]
done
clear
C)
\[y=\overline{A.B}\]
done
clear
D)
\[y=A+B\]
done
clear
View Answer play_arrow
question_answer 65) The ratio of tensile stress to the longitudinal strain is defined as
A)
Bulk modulus
done
clear
B)
Young's modulus
done
clear
C)
Shear modulus
done
clear
D)
Compressibility
done
clear
View Answer play_arrow
question_answer 66) In the case of hollow metallic sphere, without any change inside the sphere, electric potential (V) changes with respect to distance (r) from the centre as
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Answer play_arrow
question_answer 67) An electric charge of \[8.85\times {{10}^{-13}}C\] is placed at the centre of a sphere of radius \[1\text{ }m\]. The electric flux through the sphere is
A)
\[0.2\,\,N{{C}^{-1}}\,{{m}^{2}}\]
done
clear
B)
\[0.1\,\,N{{C}^{-1}}\,{{m}^{2}}\]
done
clear
C)
\[0.3\,\,N{{C}^{-1}}\,{{m}^{2}}\]
done
clear
D)
\[0.01\,\,N{{C}^{-1}}\,{{m}^{2}}\]
done
clear
View Answer play_arrow
question_answer 68) An electric dipole is placed in an uniform electric field with the dipole axis making an angle \[\theta \] with the direction of the electric field. The orientation of the dipole for stable equilibrium is
A)
\[\frac{\pi }{6}\]
done
clear
B)
\[\frac{\pi }{3}\]
done
clear
C)
\[0\]
done
clear
D)
\[\frac{\pi }{2}\]
done
clear
View Answer play_arrow
question_answer 69) The escape velocity of a body on the surface of earth is \[11.2\text{ }km/s\]. If the earth's mass increases to twice its present value and the radius of the earth becomes half, the escape velocity would become
A)
\[5.6\,\,km/s\]
done
clear
B)
\[11.2\,\,km/s\]
done
clear
C)
\[44.8\,\,km/s\]
done
clear
D)
\[22.4\,\,km/s\]
done
clear
View Answer play_arrow
question_answer 70) Consider earth to be a sphere of mass M and radius R. The acceleration due to gravity at a depth d below the earth's surface \[({{g}_{d}})\] is
A)
\[{{g}_{d}}=g\left\{ 1-\frac{d}{R} \right\}\]
done
clear
B)
\[{{g}_{d}}=g\left\{ 1-\frac{2d}{R} \right\}\]
done
clear
C)
\[{{g}_{d}}=g\]
done
clear
D)
\[{{g}_{d}}=g\left\{ 1+\frac{d}{R} \right\}\]
done
clear
View Answer play_arrow
question_answer 71) An orbiting satellite has
A)
only kinetic energy
done
clear
B)
only potential energy
done
clear
C)
kinetic and potential energies
done
clear
D)
zero energy
done
clear
View Answer play_arrow
question_answer 72) \[x(t)=A\,\,\cos (\omega t+\phi )\]is the equation of simple harmonic motion. In this equation \[\phi \]is called
A)
phase constant
done
clear
B)
frequency
done
clear
C)
amplitude
done
clear
D)
displacement
done
clear
View Answer play_arrow
question_answer 73) The transfer characteristics of a base biased transistor has the operation regions, namely, cut-off, active region and saturation region. For using the transistor as an amplifier it has to operate in the
A)
active region
done
clear
B)
cut-off region
done
clear
C)
sturation region
done
clear
D)
cut-off and saturation
done
clear
View Answer play_arrow
question_answer 74) In which, of the following figures, the p-n diode is forward biased?
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Answer play_arrow
question_answer 75) The pn-junction which generates an emf when solar radiation falls on it, with no external bias applied, is a
A)
light emitting diode
done
clear
B)
Photodiode
done
clear
C)
solar cell
done
clear
D)
zener diode
done
clear
View Answer play_arrow
question_answer 76) In which of the following compounds, carbon exhibits a valency of 4 but oxidation state -2?
A)
\[C{{H}_{3}}Cl\]
done
clear
B)
\[CHC{{l}_{3}}\]
done
clear
C)
\[C{{H}_{2}}C{{l}_{2}}\]
done
clear
D)
\[HCHO\]
done
clear
View Answer play_arrow
question_answer 77) Which one of the following is correct?
A)
Equivalent conductance decreases with dilution
done
clear
B)
Specific conductance increases with dilution
done
clear
C)
Specific conductance decreases with dilution
done
clear
D)
Equivalent conductance increases with increasing concentration
done
clear
View Answer play_arrow
question_answer 78) A cell is constituted by coupling the two electrodes \[\text{Sn/S}{{\text{n}}^{\text{2+}}}\]and \[Cu/C{{u}^{2+}}.\] If \[{{E}^{o}}(S{{n}^{2+}},Sn),{{E}^{o}}(C{{u}^{2+}},Cu)\]and \[{{E}^{o}}\](cell) are \[-0.14\,V,0.34\,V\]and 0.48 V respectively, the correct representation of the cell is
A)
\[Sn(s)|S{{n}^{2+}}(0.1\,M)||C{{u}^{2+}}(1.0\,M)|Cu(s)\]
done
clear
B)
\[Sn(s)|S{{n}^{2+}}(1.0\,M)||C{{u}^{+}}(1.0\,M)|Cu(s)\]
done
clear
C)
\[Sn(s)|S{{n}^{2+}}(1.0\,M)||C{{u}^{2+}}(1.0\,M)|Cu(s)\]
done
clear
D)
\[Cu(s)|C{{u}^{2+}}(1.0\,M)||S{{n}^{2+}}(1.0\,M)|Sn(s)\]
done
clear
View Answer play_arrow
question_answer 79) Chemically unreactive three different gases A, B and C of molecular masses 16, 32 and 64 are enclosed in a vessel at constant temperature till equilibrium is reached. Which of the following statements is true?
A)
Gas A will be at the top of the vessel
done
clear
B)
Gas C will be at the top of the vessel
done
clear
C)
Gas C will be at the bottom of the vessel
done
clear
D)
Gases will form homogeneous mixture
done
clear
View Answer play_arrow
question_answer 80) Among the following which one is a linear molecule having zero dipole moment?
A)
\[{{H}_{2}}O\]
done
clear
B)
\[HCl\]
done
clear
C)
\[C{{O}_{2}}\]
done
clear
D)
\[{{H}_{2}}S\]
done
clear
View Answer play_arrow
question_answer 81) The bond order of\[{{\text{C}}_{\text{2}}}\]molecule is
A)
1
done
clear
B)
2
done
clear
C)
0
done
clear
D)
3
done
clear
View Answer play_arrow
question_answer 82) Among the following, the compound that is readily soluble in water is
A)
\[BeS{{O}_{4}}\]
done
clear
B)
\[CaS{{O}_{4}}\]
done
clear
C)
\[SrS{{O}_{4}}\]
done
clear
D)
\[BaS{{O}_{4}}\]
done
clear
View Answer play_arrow
question_answer 83) The oxyacid of sulphur that contains a lone pair of electrons on sulphur is
A)
sulphurous acid
done
clear
B)
sulphuric acid
done
clear
C)
peroxodisulphuric acid
done
clear
D)
pyrosulphuric acid
done
clear
View Answer play_arrow
question_answer 84) The hybridization involved in\[\text{PC}{{\text{l}}_{\text{5}}}\] is
A)
\[s{{p}^{3}}d\]
done
clear
B)
\[s{{p}^{3}}{{d}^{2}}\]
done
clear
C)
\[{{d}^{2}}s{{p}^{2}}\]
done
clear
D)
\[s{{p}^{3}}\]
done
clear
View Answer play_arrow
question_answer 85) In which of the following molecules the central atom has two lone pairs of electrons?
A)
\[S{{F}_{4}}\]
done
clear
B)
\[Br{{F}_{5}}\]
done
clear
C)
\[S{{O}_{2}}\]
done
clear
D)
\[Xe{{F}_{4}}\]
done
clear
View Answer play_arrow
question_answer 86) The correct order of reducing character of alkali metals is
A)
\[Rb<K<Na<Li\]
done
clear
B)
\[Li<Na<K<Rb\]
done
clear
C)
\[Na<K<Rb<Li\]
done
clear
D)
\[Rb<Na<K<Li\]
done
clear
View Answer play_arrow
question_answer 87) The paramagnetic oxides of nitrogen are
A)
dinitrogen monoxide and nitrogen monoxide
done
clear
B)
nitrogen monoxide and nitrogen dioxide
done
clear
C)
nitrogen dioxide and dinitrogen trioxide
done
clear
D)
dinitrogen trioxide and dinitrogen tetroxide
done
clear
View Answer play_arrow
question_answer 88) Pick out the wrong statement
A)
The standard free energy of formation of elements is zero
done
clear
B)
A process that leads to increase in free energy will be spontaneous
done
clear
C)
A process accompanied by decrease in entropy will be non-spontaneous under normal conditions.
done
clear
D)
Enthalpy of combustion is always negative
done
clear
View Answer play_arrow
question_answer 89) The standard enthalpy of formation of \[{{C}_{2}}{{H}_{4}}(g),C{{O}_{2}}(g)\] and\[{{H}_{2}}O(l)\]are\[~52,-394\] and \[-284\,kJ\,mo{{l}^{-1}}\]respectively. Then the amount of heat evolved by burning 7 g of \[{{C}_{2}}{{H}_{4}}(g)\]is
A)
1412 kJ
done
clear
B)
9884 kJ
done
clear
C)
353 kJ
done
clear
D)
706 kJ
done
clear
View Answer play_arrow
question_answer 90) Which one among the following pairs does not represent, example for intensive property?
A)
temperature and density
done
clear
B)
pressure and molar volume
done
clear
C)
molar heat capacity and density
done
clear
D)
heat capacity and enthalpy
done
clear
View Answer play_arrow
question_answer 91) The values of \[\Delta H\]and \[\Delta S\]for a reaction are \[30\,\text{kJ}\,\text{mo}{{\text{l}}^{-1}}\]and-\[100\,J{{K}^{-1}}\,mo{{l}^{-1}}\] respectively. Then the temperature above which the reaction will become spontaneous is
A)
300 K
done
clear
B)
30 K
done
clear
C)
100 K
done
clear
D)
\[~300{{\,}^{o}}C\]
done
clear
View Answer play_arrow
question_answer 92) Three Faradays of electricity are passed through molten\[\text{A}{{\text{l}}_{\text{2}}}{{\text{O}}_{\text{3}}}\text{,}\]aqueous solution of \[\text{CuS}{{\text{O}}_{\text{4}}}\]and molten NaCI taken in three different electrolytic cells. Then the mole ratio of Al, Cu and Na deposited on the cathode will be
A)
3:4:6
done
clear
B)
2:1:6
done
clear
C)
3: 2: 1
done
clear
D)
2: 3 : 6
done
clear
View Answer play_arrow
question_answer 93) Which of the esters shown, after reduction with \[\text{LiAl}{{\text{H}}_{\text{4}}}\]and aqueous workup, will yield two molecules of only a single alcohol?
A)
\[{{C}_{6}}{{H}_{5}}COO{{C}_{6}}{{H}_{5}}\]
done
clear
B)
\[C{{H}_{3}}C{{H}_{2}}COOC{{H}_{2}}C{{H}_{3}}\]
done
clear
C)
\[{{C}_{6}}{{H}_{5}}COOC{{H}_{2}}{{C}_{6}}{{H}_{5}}\]
done
clear
D)
\[C{{H}_{3}}COOC{{H}_{3}}\]
done
clear
View Answer play_arrow
question_answer 94) Ethyl methyl ketone on treatment with a solution of sodium hypochlorite gives chloroform and
A)
sodium ethanoate
done
clear
B)
sodium propanoate
done
clear
C)
sodium methanoate
done
clear
D)
sodium ethoxide
done
clear
View Answer play_arrow
question_answer 95) What are the products of the following reaction \[{{C}_{6}}{{H}_{5}}OC{{H}_{2}}C{{H}_{2}}OH\xrightarrow[\text{Hear}]{\text{excess}\,\text{HBr}}\]
A)
\[{{C}_{6}}{{H}_{5}}OH+BrC{{H}_{2}}C{{H}_{2}}Br\]
done
clear
B)
\[{{C}_{6}}{{H}_{5}}OH+HOC{{H}_{2}}C{{H}_{2}}OH\]
done
clear
C)
\[{{C}_{6}}{{H}_{5}}Br+HOC{{H}_{2}}C{{H}_{2}}OH\]
done
clear
D)
\[{{C}_{6}}{{H}_{5}}OH+BrC{{H}_{2}}C{{H}_{2}}OH\]
done
clear
View Answer play_arrow
question_answer 96) The compound that gives both iodoform and Fehling's tests is
A)
ethanol
done
clear
B)
propanone
done
clear
C)
2-butanol
done
clear
D)
ethanol
done
clear
View Answer play_arrow
question_answer 97) The equilibrium constant value\[{{K}_{p}}\]for the equilibrium \[{{H}_{2}}(g)+{{I}_{2}}(g)\rightleftharpoons 2HI(g)\] changes with
A)
total pressure
done
clear
B)
temperature
done
clear
C)
catalyst
done
clear
D)
the amounts of \[{{\text{H}}_{\text{2}}}\]and\[{{\text{I}}_{\text{2}}}\]present
done
clear
View Answer play_arrow
question_answer 98) Among the following, the one which can act as both Bronsted acid as well as Bronsted base is
A)
\[{{H}_{3}}P{{O}_{4}}\]
done
clear
B)
\[AlC{{l}_{3}}\]
done
clear
C)
\[C{{H}_{3}}CO{{O}^{-}}\]
done
clear
D)
\[{{H}_{2}}O\]
done
clear
View Answer play_arrow
question_answer 99) The reaction \[A+B\to C+D+40\,kJ\]has an .activation energy of 18 kJ. Then the activation energy for the reaction\[C+D\to A+B\] is
A)
58 kJ
done
clear
B)
\[~-\text{ }40\text{ }kJ\]
done
clear
C)
\[~-\text{ }18\text{ }kJ\]
done
clear
D)
\[~22\text{ }kJ\]
done
clear
View Answer play_arrow
question_answer 100) One gram atom of a radioactive isotope \[({{t}_{1/2}}=10\,h)\]that emits alpha particle was placed in a sealed container. The time taken for 0.875 g atom of helium to accumulate in the container is
A)
10 h
done
clear
B)
20 h
done
clear
C)
30 h
done
clear
D)
40 h
done
clear
View Answer play_arrow
question_answer 101) In which one of the following reactions, the yield of the products decreases by increasing the pressure?
A)
\[2S{{O}_{2}}(g)+{{O}_{2}}(g)2S{{O}_{3}}(g)\]
done
clear
B)
\[{{N}_{2}}(g)+3{{H}_{2}}(g)2N{{H}_{3}}(g)\]
done
clear
C)
\[PC{{l}_{5}}(g)PC{{l}_{3}}(g)+C{{l}_{2}}(g)\]
done
clear
D)
\[{{N}_{2}}(g)+{{O}_{2}}(g)2NO(g)\]
done
clear
View Answer play_arrow
question_answer 102) The pH of the solution formed by mixing 20 mL of \[\text{0}\text{.05 M }{{\text{H}}_{\text{2}}}\text{S}{{\text{O}}_{\text{4}}}\]with 5.0 mL of \[\text{0}\text{.45 M NaOH}\]at 298 K is
A)
6
done
clear
B)
2
done
clear
C)
12
done
clear
D)
7
done
clear
View Answer play_arrow
question_answer 103) Zeise's salt is
A)
\[[Fe{{({{C}_{5}}{{H}_{5}})}_{2}}]\]
done
clear
B)
\[[Pb{{({{C}_{2}}{{H}_{5}})}_{4}}]\]
done
clear
C)
\[K[PtC{{l}_{3}}({{C}_{2}}{{H}_{4}})]\]
done
clear
D)
\[[Ni{{(CO)}_{4}}]\]
done
clear
View Answer play_arrow
question_answer 104) The metal used to recover copper from a solution of copper sulphate is
A)
Na
done
clear
B)
Fe
done
clear
C)
Hg
done
clear
D)
Ag
done
clear
View Answer play_arrow
question_answer 105) Which of the following is a correct name according to IUPAC rules?
A)
2, 3-diethylhexane
done
clear
B)
3-ethyl-2-methylpentane
done
clear
C)
3, 4-dimethylpentane
done
clear
D)
2-ethyl-2-methylpentane
done
clear
View Answer play_arrow
question_answer 106) The formula of siderite is
A)
\[F{{e}_{2}}{{O}_{3}}\]
done
clear
B)
\[F{{e}_{3}}{{O}_{4}}\]
done
clear
C)
\[Fe{{S}_{2}}\]
done
clear
D)
\[FeC{{O}_{3}}\]
done
clear
View Answer play_arrow
question_answer 107) When 'blue vitriol? is heated at 373 K, the product formed is
A)
\[CuS{{O}_{4}}.3{{H}_{2}}O\]
done
clear
B)
\[CuO+S{{O}_{3}}\]
done
clear
C)
\[CuS{{O}_{4}}.{{H}_{2}}O\]
done
clear
D)
\[CuS{{O}_{4}}\]
done
clear
View Answer play_arrow
question_answer 108) An alkane with a molecular formula \[{{\text{C}}_{\text{6}}}{{\text{H}}_{\text{14}}}\]reacts with chlorine in the presence of light and heat to give two constitutionally isomeric monochlorides of molecular formula \[{{\text{C}}_{\text{6}}}{{\text{H}}_{\text{13}}}\text{Cl}\text{.}\]What is the most reasonable starting alkane?
A)
\[n-\]hexane
done
clear
B)
2, 2-dimethylbutane
done
clear
C)
2, 3-dimethylbutane
done
clear
D)
3-methylpentane
done
clear
View Answer play_arrow
question_answer 109) Which of the following statements are correct with respect to the effect of trifluoromethyl group\[(-C{{F}_{3}}),\]on an electrophilic aromatic substitution?
A)
The \[\text{C}{{\text{F}}_{\text{3}}}\]group will deactivate the ring
done
clear
B)
The\[\text{C}{{\text{F}}_{\text{3}}}\] group will activate the ring
done
clear
C)
The \[\text{C}{{\text{F}}_{\text{3}}}\]group will be ortho, para director
done
clear
D)
The \[\text{C}{{\text{F}}_{\text{3}}}\]group will be a meta director
done
clear
View Answer play_arrow
question_answer 110) Which of the following compound is chiral?
A)
3-pentanol
done
clear
B)
1-pentanol
done
clear
C)
3-methyl-l-butanol
done
clear
D)
3-methyl-2-butanol
done
clear
View Answer play_arrow
question_answer 111) Which one among the following is most reactive towards electrophilic substitution reaction?
A)
Aniline
done
clear
B)
Nitrobenzene
done
clear
C)
Benzoicacid
done
clear
D)
Acetanilide
done
clear
View Answer play_arrow
question_answer 112) Which one of the following is not aromatic?
A)
Cyclopentadienyl anion
done
clear
B)
Cycloheptatrienyl cation
done
clear
C)
Cyclooctatetraene
done
clear
D)
Thiophene
done
clear
View Answer play_arrow
question_answer 113) The separation of racemic mixture into the pure enantiomers is termed as
A)
racemiscition
done
clear
B)
resolution
done
clear
C)
equilibration
done
clear
D)
isomerization
done
clear
View Answer play_arrow
question_answer 114) In a reaction \[2A+B\to {{A}_{2}}B,\]the reactant B will disappear at
A)
half the rate as A will decrease
done
clear
B)
the same rate as A will decrease
done
clear
C)
twice the rate as A will decrease
done
clear
D)
half the rate as \[{{A}_{2}}B\]will form
done
clear
View Answer play_arrow
question_answer 115) Which one of the following liquid pairs will exhibit a positive deviation from Raoult?s law?
A)
\[n-\]hexane and n-heptane
done
clear
B)
ethanol and chloroform
done
clear
C)
phenol and aniline
done
clear
D)
chloroform and acetone
done
clear
View Answer play_arrow
question_answer 116) The van't Hoff factor ?i? for a dilute aqueous solution of sucrose is
A)
zero
done
clear
B)
1.0
done
clear
C)
1.5
done
clear
D)
2.0
done
clear
View Answer play_arrow
question_answer 117) The unit of rate constant for a zero order reaction is
A)
\[{{s}^{-1}}\]
done
clear
B)
\[\text{mol}\,\text{L}{{\text{s}}^{-1}}\]
done
clear
C)
\[mol\,{{L}^{-1}}{{s}^{-1}}\]
done
clear
D)
no unit
done
clear
View Answer play_arrow
question_answer 118) When a solution containing non-volatile solute is diluted with water
A)
its osmotic pressure increases
done
clear
B)
its boiling point increases
done
clear
C)
its freezing point decreases
done
clear
D)
its vapour pressure increases
done
clear
View Answer play_arrow
question_answer 119) What happens when blood cells are placed in pure water?
A)
The fluid in blood cells rapidly moves into water
done
clear
B)
The water molecules rapidly move into blood cells
done
clear
C)
The blood cells dissolve in water
done
clear
D)
No change takes place
done
clear
View Answer play_arrow
question_answer 120) Mendius reaction converts an alkyi cyanide to
A)
a primary amine
done
clear
B)
an aldehyde
done
clear
C)
a ketone
done
clear
D)
an oxime
done
clear
View Answer play_arrow
question_answer 121) Which one of the following amines cannot be prepared by Gabriel's synthesis?
A)
Butylamine
done
clear
B)
Isobutylamine
done
clear
C)
2-phenylethylamine
done
clear
D)
N-methylbenzylamine
done
clear
View Answer play_arrow
question_answer 122) Which one of the following is not an aldose?
A)
Glucose
done
clear
B)
Ribose
done
clear
C)
Fructose
done
clear
D)
Mannose
done
clear
View Answer play_arrow
question_answer 123) Which one of the following is a secondary amine?
A)
2-butanamine
done
clear
B)
N-methylpiperidine
done
clear
C)
N-methyl-2-pentanamine
done
clear
D)
p-anisidine
done
clear
View Answer play_arrow
question_answer 124) The weakest base among the following is
A)
dimethylamine
done
clear
B)
aniline
done
clear
C)
methylamine
done
clear
D)
ethylamine
done
clear
View Answer play_arrow
question_answer 125) Which one of the following is not a green house gas?
A)
Methane
done
clear
B)
Ozone
done
clear
C)
Carbon dioxide
done
clear
D)
Nitrogen
done
clear
View Answer play_arrow
question_answer 126) The lanthanide element that has the electronic configuration, \[[Xe]4{{f}^{7}}5{{d}^{1}}6{{s}^{2}}\]is
A)
lutetium
done
clear
B)
terbium
done
clear
C)
ytterbium
done
clear
D)
gadolinium
done
clear
View Answer play_arrow
question_answer 127) The transition metal ion that has 'spin-only magnetic moment value of 5.96 is
A)
\[M{{n}^{2+}}\]
done
clear
B)
\[F{{e}^{2+}}\]
done
clear
C)
\[{{V}^{2+}}\]
done
clear
D)
\[C{{u}^{2+}}\]
done
clear
View Answer play_arrow
question_answer 128) Square planar complexes of the type MABXL (where A, B, X and L are unidentates) show
A)
two \[cis\]and one trans isomer
done
clear
B)
two trans and one \[cis\] isomer
done
clear
C)
two \[cis\]and two trans isomer
done
clear
D)
one \[cis\]and one trans isomer
done
clear
View Answer play_arrow
question_answer 129) The alloy of copper that contains zinc is
A)
monel metal
done
clear
B)
bronze
done
clear
C)
bell metal
done
clear
D)
brass
done
clear
View Answer play_arrow
question_answer 130) All \[\text{Cu (II)}\]halides are known except the iodide. The reason for is that
A)
iodide is a bulky ion
done
clear
B)
\[\text{C}{{\text{u}}^{\text{2+}}}\]oxidizes iodide to iodine
done
clear
C)
\[\text{C}{{\text{u}}^{\text{2+}}}\] (aq) has much more negative hydration enthalpy
done
clear
D)
\[\text{C}{{\text{u}}^{\text{2+}}}\]ion has smaller size
done
clear
View Answer play_arrow
question_answer 131) Among the following the ambidentate ligand is
A)
\[{{H}_{2}}NC{{H}_{2}}C{{H}_{2}}N{{H}_{2}}\]
done
clear
B)
\[CO_{3}^{2-}\]
done
clear
C)
\[NO_{2}^{-}\]
done
clear
D)
\[{{C}_{2}}O_{4}^{2-}\]
done
clear
View Answer play_arrow
question_answer 132) Among the following, which one is paramagnetic and has tetrahedral geometry?
A)
\[{{[Ni{{(CN)}_{4}}]}^{2-}}\]
done
clear
B)
\[{{[NiC{{l}_{4}}]}^{2-}}\]
done
clear
C)
\[[Ni{{(CO)}_{4}}]\]
done
clear
D)
\[{{[CoC{{l}_{2}}{{(en)}_{2}}]}^{+}}\]
done
clear
View Answer play_arrow
question_answer 133) The de-Broglie wavelength of a ball of mass 10 g moving with a velocity of \[10\,\text{m}{{\text{s}}^{-1}}\]is \[[h=6.626\times {{10}^{-34}}Js]\]
A)
\[6.626\times {{10}^{-33}}\,m\]
done
clear
B)
\[6.626\times {{10}^{-29}}\,m\]
done
clear
C)
\[6.626\times {{10}^{-31}}\,m\]
done
clear
D)
\[6.626\times {{10}^{-36}}\,m\]
done
clear
View Answer play_arrow
question_answer 134) The electrons identified by quantum numbers n and I, (i) \[n=4,l=1,\](ii)\[~n=4,l=0\] (iii) \[n=3,l=2\]and (iv) \[n=3,l=1\]can be placed in order of increasing energy as
A)
(i) < (ii) < (iii) < (iv)
done
clear
B)
(iv) < (iii) < (ii) < (i)
done
clear
C)
(iv) < (ii) < (iii) < (i)
done
clear
D)
(iv) < (i) < (ii) < (iii)
done
clear
View Answer play_arrow
question_answer 135) A radioactive element\[_{\text{92}}^{\text{238}}\text{M}\]emits one alpha particle followed by two beta particles. Then the daughter element formed is
A)
an isotope
done
clear
B)
an isobar
done
clear
C)
an isotone
done
clear
D)
an isodiaphere
done
clear
View Answer play_arrow
question_answer 136) When 6.3 g of sodium bicarbonate are added to 30.0 g of acetic acid solution, the residual solution is found to weigh 33.0 g. The mass of carbon dioxide released in the reaction is
A)
3.0 g
done
clear
B)
0.91 g
done
clear
C)
1.91 g
done
clear
D)
3.3 g
done
clear
View Answer play_arrow
question_answer 137) Two oxides of a metal contain 36.4% and 53.4% of oxygen by mass respectively. If the formula of the first oxide is \[{{\text{M}}_{\text{2}}}\text{O,}\]then that of the second is
A)
\[{{M}_{2}}{{O}_{3}}\]
done
clear
B)
\[MO\]
done
clear
C)
\[M{{O}_{2}}\]
done
clear
D)
\[{{M}_{2}}{{O}_{5}}\]
done
clear
View Answer play_arrow
question_answer 138) In a volumetric experiment, it was found that a solution of\[\text{KMn}{{\text{O}}_{\text{4}}}\]is reduced to\[\text{MnS}{{\text{O}}_{\text{4}}}\text{.}\]If the normality of the solution is 1.0 N, then the molarity of the solution will be
A)
0.5 M
done
clear
B)
0.2 M
done
clear
C)
1.0 M
done
clear
D)
0.4 M
done
clear
View Answer play_arrow
question_answer 139) Which of the following pair of gases will diffuse at the same rate through a porous plug?
A)
\[CO,N{{O}_{2}}\]
done
clear
B)
\[NO,{{C}_{2}}{{H}_{6}}\]
done
clear
C)
\[N{{O}_{2}},C{{O}_{2}}\]
done
clear
D)
\[N{{H}_{3}},P{{H}_{3}}\]
done
clear
View Answer play_arrow
question_answer 140) Freundlich adsorption isotherm equation is
A)
\[\log \frac{m}{x}=\log K+\frac{1}{m}\log p\]
done
clear
B)
\[\log \frac{x}{m}=\log K+n\log p\]
done
clear
C)
\[\log \frac{m}{x}=\log K+n\log p\]
done
clear
D)
\[\log \frac{x}{m}=\log K+\frac{1}{n}\log p\]
done
clear
View Answer play_arrow
question_answer 141) Which one of the following is a copolymer formed by condensation polymerization?
A)
Terylene
done
clear
B)
Buna-S
done
clear
C)
Buna-N
done
clear
D)
Neoprene
done
clear
View Answer play_arrow
question_answer 142) Which of the following is the largest is size?
A)
\[C{{l}^{-}}\]
done
clear
B)
\[{{S}^{2-}}\]
done
clear
C)
\[N{{a}^{+}}\]
done
clear
D)
\[{{F}^{-}}\]
done
clear
View Answer play_arrow
question_answer 143) In zinc blende structure, the coordination number of the cation is
A)
4
done
clear
B)
6
done
clear
C)
8
done
clear
D)
12
done
clear
View Answer play_arrow
question_answer 144) The best coagulant for the precipitation of \[\text{Fe(OH}{{\text{)}}_{\text{3}}}\]is
A)
\[N{{a}_{2}}HP{{O}_{3}}\]
done
clear
B)
\[NaN{{O}_{3}}\]
done
clear
C)
\[N{{a}_{3}}P{{O}_{4}}\]
done
clear
D)
\[N{{a}_{2}}S{{O}_{4}}\]
done
clear
View Answer play_arrow
question_answer 145) The second ionization energies of Li, Be, B and C are in the order
A)
\[Li>C>B>Be\]
done
clear
B)
\[Li>B>C>Be\]
done
clear
C)
\[B>C>Be>Li\]
done
clear
D)
\[Be>C>B>Li\]
done
clear
View Answer play_arrow
question_answer 146) Chloroform on heating with silver powder gives
A)
ethene
done
clear
B)
ethyne
done
clear
C)
methane
done
clear
D)
ehane
done
clear
View Answer play_arrow
question_answer 147) The decreasing order of acidity among the compounds, ethanol (I) 2, 2, 2-trifluoroethanol (II), trifiuroacetic acid (III) and acetic acid (IV) is
A)
\[III>II>IV>I\]
done
clear
B)
\[IV>III>II>I\]
done
clear
C)
\[~I>II>III>IV\]
done
clear
D)
\[III>IV>II>I\]
done
clear
View Answer play_arrow
question_answer 148) Which of the following is most acidic?
A)
Methane
done
clear
B)
Ethane
done
clear
C)
Ethyne
done
clear
D)
Ethene
done
clear
View Answer play_arrow
question_answer 149) 1-chlorobutane on reaction with alcoholic potash gives
A)
1-butanol
done
clear
B)
2-butene
done
clear
C)
1-butene
done
clear
D)
2-butanol
done
clear
View Answer play_arrow
question_answer 150) Phenol on heating with alcoholic KOH and chloroform -undergoes
A)
Reimer-Tiemann reaction
done
clear
B)
Kolbe reaction
done
clear
C)
Gattermann reaction
done
clear
D)
Cannizzaro reaction
done
clear
View Answer play_arrow
question_answer 151) The ratio in which ZX-plane divides the line segment AB joining the points \[A(4,2,3)\] and \[B(-2,4,5)\] is equal to
A)
\[1:2\] internally
done
clear
B)
\[1:2\] externally
done
clear
C)
\[-1:2\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 152) The projection of a line segment OP through origin O, on the coordinate axes are 8, 5, 6. Then, the length of the line segment OP is equal to
A)
\[5\]
done
clear
B)
\[5\sqrt{5}\]
done
clear
C)
\[10\sqrt{5}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 153) The length of the perpendicular distance of the point \[(-1,\,4,\,0)\] from the line \[\frac{x}{1}=\frac{y}{3}=\frac{z}{1}\] is equal to
A)
\[\sqrt{6}\]
done
clear
B)
\[\sqrt{5}\]
done
clear
C)
\[2\]
done
clear
D)
\[1\]
done
clear
View Answer play_arrow
question_answer 154) The number of lines making equal angles with the coordinate axes in three dimensional geometry is equal to
A)
3
done
clear
B)
4
done
clear
C)
2
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 155) Suppose \[P(2,\,y,\,z)\] lies on the line through \[A(3,-1,4)\] and \[B(-4,2,1)\]. Then, the value of z is equal to
A)
\[\frac{-1}{2}\]
done
clear
B)
\[\frac{19}{4}\]
done
clear
C)
\[\frac{-19}{4}\]
done
clear
D)
\[\frac{25}{7}\]
done
clear
View Answer play_arrow
question_answer 156) The equation of the plane perpendicular to the Z-axis and passing through \[(2,-3,5)\] is
A)
\[x-2=0\]
done
clear
B)
\[y+3=0\]
done
clear
C)
\[z-5=0\]
done
clear
D)
\[2x-3y+5z+4=0\]
done
clear
View Answer play_arrow
question_answer 157) The value of \[\sum\limits_{n=0}^{\infty }{\frac{{{n}^{2}}+4}{n\,!}}\]is equal to
A)
\[6\,e\]
done
clear
B)
\[5\,e\]
done
clear
C)
\[4\,e\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 158) The three distinct points \[A(at_{1}^{2},\,2a{{t}_{1}}),\,\,B(at_{2}^{2},\,\,2a{{t}_{2}})\]and \[C(0,\,a)\](where a is a real number) are collinear, if
A)
\[{{t}_{1}}{{t}_{2}}=-1\]
done
clear
B)
\[{{t}_{1}}{{t}_{2}}=1\]
done
clear
C)
\[2{{t}_{1}}{{t}_{2}}={{t}_{1}}+{{t}_{2}}\]
done
clear
D)
\[{{t}_{1}}+{{t}_{2}}=a\]
done
clear
View Answer play_arrow
question_answer 159) The equation of the line passing through \[(0,0)\]and intersection of \[3x-4y=2\]and \[x+2y=-4\]is
A)
\[7x=6y\]
done
clear
B)
\[6x=7y\]
done
clear
C)
\[5x=8y\]
done
clear
D)
\[x=0\]
done
clear
View Answer play_arrow
question_answer 160) The value of k for which the equation \[{{x}^{2}}-4xy-{{y}^{2}}+6x+2y+k=0\] represents a pair of straight lines is
A)
\[k=4\]
done
clear
B)
\[k=-1\]
done
clear
C)
\[k=\frac{-4}{5}\]
done
clear
D)
\[k=\frac{-22}{5}\]
done
clear
View Answer play_arrow
question_answer 161) If the values observed are \[1,\text{ }2,\text{ }3,\text{ }...,\text{ }n\]each with frequency 1 and n is even, then the mean deviation from mean equals to
A)
\[n\]
done
clear
B)
\[\frac{n}{2}\]
done
clear
C)
\[\frac{n}{4}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 162) A line segment of 8 units in length moves so that its end points are always on the coordinate axes. Then, the equation of locus of its mid-point is
A)
\[{{x}^{2}}+{{y}^{2}}=4\]
done
clear
B)
\[{{x}^{2}}+{{y}^{2}}=16\]
done
clear
C)
\[{{x}^{2}}+{{y}^{2}}=8\]
done
clear
D)
\[|x|+|y|=8\]
done
clear
View Answer play_arrow
question_answer 163) The number of straight lines which can be drawn through the point \[(-2,\,\,\,2)\] so that its distance from \[(-3,\,\,1)\] will be equal 6 units is
A)
one
done
clear
B)
two
done
clear
C)
infinite
done
clear
D)
zero
done
clear
View Answer play_arrow
question_answer 164) The maximum and minimum magnitude of resultants of two forces are \[{{P}_{1}}\] and \[{{P}_{2}}\]respectively. The magnitude of the resultant when two forces are at right angles is equal to
A)
\[2\sqrt{{{P}_{1}}{{P}_{2}}}\]
done
clear
B)
\[\sqrt{P_{1}^{2}\,+P_{2}^{2}}\]
done
clear
C)
\[\frac{\sqrt{P_{1}^{2}\,+P_{2}^{2}}}{2}\]
done
clear
D)
\[\sqrt{\frac{P_{1}^{2}\,+P_{2}^{2}}{2}}\]
done
clear
View Answer play_arrow
question_answer 165) The distance travelled by a bus in t seconds after the brakes are applied is \[1+2t-2{{t}^{2}}m.\] The distance travelled by the bus before it stops is equal to
A)
\[0.5\text{ }m\]
done
clear
B)
\[1\,\,m\]
done
clear
C)
\[1.5\,\,m\]
done
clear
D)
\[2.5\,\,m\]
done
clear
View Answer play_arrow
question_answer 166) Two balls are projected from the same point in directions inclined at \[{{45}^{o}}\] and \[{{60}^{o}}\] to the horizontal respectively. If they attain the same height, the ratio of their velocities of projection is equal to
A)
\[\sqrt{3}:1\]
done
clear
B)
\[3:1\]
done
clear
C)
\[3:2\]
done
clear
D)
\[3:2\]
done
clear
View Answer play_arrow
question_answer 167) A force 2 unite acts along the line \[x-4=y-5.\] The moment of the force about the point \[(1,\,\,1)\] along Z-axis is equal to
A)
\[0\]
done
clear
B)
\[\frac{1}{\sqrt{2}}\]
done
clear
C)
\[\sqrt{2}\]
done
clear
D)
\[2\sqrt{2}\]
done
clear
View Answer play_arrow
question_answer 168) A particle is thrown vertically upwards with velocity \[24.5\text{ }cm/min\]. It will return to the original position after
A)
\[1\,s\]
done
clear
B)
\[3\,\,s\]
done
clear
C)
\[1.5\,\,s\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 169) The area of the triangle whose vertices are the points \[(a(a+1),\,a+1),\,\,((a+1)\,(a+2),\]\[a+2)\] and \[((a+2)\,(a+3),\,(a+3)\]is equal to
A)
\[-1\]
done
clear
B)
\[1\]
done
clear
C)
\[1/2\]
done
clear
D)
\[a(a+1)\,(a+2)\,(a+3)\]
done
clear
View Answer play_arrow
question_answer 170) If A is a \[2\times 2\] matrix and \[|A|=2,\] then the matrix represented by A (adj A) is equal to
A)
\[\left[ \begin{matrix} 1 & 0 \\ 0 & 1 \\ \end{matrix} \right]\]
done
clear
B)
\[\left[ \begin{matrix} 2 & 0 \\ 0 & 2 \\ \end{matrix} \right]\]
done
clear
C)
\[\left[ \begin{matrix} 1/2 & 0 \\ 0 & 1/2 \\ \end{matrix} \right]\]
done
clear
D)
\[\left[ \begin{matrix} 0 & 2 \\ 2 & 0 \\ \end{matrix} \right]\]
done
clear
View Answer play_arrow
question_answer 171) . Let a and b be the position vector of A and B respectively. The position vector of a point C on AB produced, such that \[AC=4\text{ }AB\]is equal to
A)
\[\frac{4b-a}{3}\]
done
clear
B)
\[4b-3a\]
done
clear
C)
\[4a-3b\]
done
clear
D)
\[\frac{4a-b}{3}\]
done
clear
View Answer play_arrow
question_answer 172) The matrix product satisfies \[[5\,\,\,\,6\,\,\,\,\,2].\,\,{{A}^{T}}=[4\,\,8\,\,\,1\,\,\,7\,\,\,8],\] where \[{{A}^{T}}\]denotes the transpose of the matrix A. Then, the order of the matrix A equals to
A)
\[1\times 2\]
done
clear
B)
\[5\times 1\]
done
clear
C)
\[3\times 5\]
done
clear
D)
\[5\times 3\]
done
clear
View Answer play_arrow
question_answer 173) Let A and B both be \[3\times 3\] matrices. Then, \[{{(AB)}^{T}}=BA,\]if
A)
A is skew-symmetric and B is symmetric
done
clear
B)
B is skew-symmetric and A is symmetric
done
clear
C)
A and B are skew-symmetric
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 174) Let \[A=\{1,\,2\},\] \[B=\{\{1\},\,\,\,\{2\}\},\] \[C=\{\{1\}\,\,\{1,\,\,2\}\}.\] Then, which of the following relation is true?
A)
\[A=B\]
done
clear
B)
\[B\subseteq C\]
done
clear
C)
\[A\in C\]
done
clear
D)
\[A\subset C\]
done
clear
View Answer play_arrow
question_answer 175) If \[f(x)=3-x,-4\le x\le 4,\]then the domain of \[{{\log }_{e}}\,(f\,(x))\] is
A)
\[[-4,\,\,4]\]
done
clear
B)
\[(-\,\infty ,\,\,3]\]
done
clear
C)
\[(-\,\infty ,\,\,3)\]
done
clear
D)
\[[-4,\,\,\,3)\]
done
clear
View Answer play_arrow
question_answer 176) If \[\omega \] denotes the imaginary cube roots of unity. Then, the roots of the equation \[{{(x+1)}^{3}}+8=0\] are
A)
\[-3,\,1+2\omega ,\,1+2{{\omega }^{2}}\]
done
clear
B)
\[-3,\,1-2\,\omega ,\,1-2{{\omega }^{2}}\]
done
clear
C)
\[-3,-1+2\omega ,-1+2{{\omega }^{2}}\]
done
clear
D)
\[-3,-1-2\omega ,-1-2{{\omega }^{2}}\]
done
clear
View Answer play_arrow
question_answer 177) The function \[f:[0,\,\,\infty )\to [0,\,\,\infty )\] defined by \[f\,(x)=\frac{2x}{1+2x}\]is
A)
one-one and onto
done
clear
B)
one-one but not onto
done
clear
C)
not one-one but onto
done
clear
D)
neither one-one nor onto
done
clear
View Answer play_arrow
question_answer 178) If \[{{z}_{r}}=\cos \,\left( \frac{\pi }{{{3}^{r}}} \right)+i\,\,\sin \left( \frac{\pi }{{{3}^{r}}} \right),\]then \[{{z}_{1}}.{{z}_{2}}.{{z}_{3}}....\] to \[\infty \] is equal to
A)
\[-1\]
done
clear
B)
\[0\]
done
clear
C)
\[-\,\,i\]
done
clear
D)
\[i\]
done
clear
View Answer play_arrow
question_answer 179) If \[\sin \,\,\theta \]and \[\cos \,\,\theta \] are the roots of the equation \[a{{x}^{2}}+bx+c=0,\,\,\,\,\,a\ne 0,\] then the relation between the coefficients of the equation is
A)
\[{{a}^{2}}-{{b}^{2}}+2ac=0\]
done
clear
B)
\[{{a}^{2}}+{{b}^{2}}+2ac=0\]
done
clear
C)
\[\,{{a}^{2}}-{{b}^{2}}-2ac=0\]
done
clear
D)
\[{{a}^{2}}+{{b}^{2}}-2ac=0\]
done
clear
View Answer play_arrow
question_answer 180) If \[f(x)\,=kx\,-\,\cos \,x\] is monotonically increasing for all \[x\in R,\] then
A)
\[k>-1\]
done
clear
B)
\[k>-1\]
done
clear
C)
\[k>1\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 181) The value of the integral \[\int{\frac{1}{{{e}^{2s}}+{{e}^{-2x}}}}\,\,dx\] is equal to
A)
\[2\,{{\tan }^{-1}}\,({{e}^{2x}})+C\]
done
clear
B)
\[{{\tan }^{-1}}\,({{e}^{2x}})+C\]
done
clear
C)
\[\frac{1}{2}{{\tan }^{-1}}\,({{e}^{2x}})+C\]
done
clear
D)
\[\frac{-1}{{{({{e}^{2x}}+{{e}^{-2x}})}^{2}}}+C\]
done
clear
View Answer play_arrow
question_answer 182) The value of \[\int_{4}^{8}{\frac{\sqrt{x}}{\sqrt{x}+\sqrt{12}-x}}\,\,dx\] is equal to
A)
\[4\]
done
clear
B)
\[2\]
done
clear
C)
\[1\]
done
clear
D)
\[1/2\]
done
clear
View Answer play_arrow
question_answer 183) If \[f(x)=2{{x}^{2}}-|x|+4,\,\,\,x\in [-1,2]\] Then, for some \[c\,\in \,(-1,\,2),\,\,f'(c)\] is equal to
A)
\[\frac{f(2)-f(0)}{2-0}\]
done
clear
B)
\[\frac{f(2)-f(-1)}{2-(-1)}\]
done
clear
C)
\[\frac{f(1)-f(-1)}{1-(-1)}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 184) The value of the integral \[\int{\frac{-x\,\,{{e}^{x}}}{{{(x+1)}^{2}}}}\,\,\,dx\] is equal to
A)
\[\frac{-{{e}^{x}}}{(x+1)}+C\]
done
clear
B)
\[\frac{{{e}^{x}}}{{{(x+1)}^{2}}}+C\]
done
clear
C)
\[\frac{{{e}^{x}}}{(x+1)}+C\]
done
clear
D)
\[\frac{-{{e}^{x}}}{x+1}+C\]
done
clear
View Answer play_arrow
question_answer 185) If the straight line \[y=2x+c\]is a tangent to the ellipse \[\frac{{{x}^{2}}}{3}+\frac{{{y}^{2}}}{4}=1,\] then c equals to
A)
\[\pm \,\,4\]
done
clear
B)
\[\pm \,\,6\]
done
clear
C)
\[\pm \,\,8\]
done
clear
D)
\[\pm \,\,1\]
done
clear
View Answer play_arrow
question_answer 186) The value of \[\cos \frac{\pi }{7}.\,\cos \frac{2\pi }{7}.\,\cos \frac{4\pi }{7}\] is equal to
A)
\[\frac{1}{2}\]
done
clear
B)
\[-\frac{1}{4}\]
done
clear
C)
\[\frac{1}{8}\]
done
clear
D)
\[-\frac{1}{8}\]
done
clear
View Answer play_arrow
question_answer 187) The rational number among the following real numbers is
A)
\[\sin \,\,{{15}^{o}}\]
done
clear
B)
\[\cos \,\,{{15}^{o}}\]
done
clear
C)
\[sin\,{{15}^{o}}.\,\cos \,{{15}^{o}}\]
done
clear
D)
\[sin\,{{15}^{o}}.\,\cos \,{{75}^{o}}\]
done
clear
View Answer play_arrow
question_answer 188) Suppose the straight line \[x+y=5\]touches the circle \[{{x}^{2}}+{{y}^{2}}-2x-4y+3=0\]. Then, the coordinates of the point of contact are
A)
\[(3,2)\]
done
clear
B)
\[(2,3)\]
done
clear
C)
\[(4,1)\]
done
clear
D)
\[(1,4)\]
done
clear
View Answer play_arrow
question_answer 189) \[f(x)=|\sin \,2x|+|\cos \,2x|\] is a periodic function with period
A)
\[\pi \]
done
clear
B)
\[\frac{\pi }{2}\]
done
clear
C)
\[\frac{\pi }{4}\]
done
clear
D)
\[\frac{\pi }{8}\]
done
clear
View Answer play_arrow
question_answer 190) Let C be right angle of a \[\Delta \,ABC,\] then \[\frac{{{\sin }^{2}}A}{{{\sin }^{2}}B}-\frac{{{\cos }^{2}}A}{{{\cos }^{2}}B}\] is equal to
A)
\[\frac{{{a}^{2}}-{{b}^{2}}}{ab}\]
done
clear
B)
\[\frac{{{a}^{4}}-{{b}^{4}}}{{{a}^{2}}{{b}^{2}}}\]
done
clear
C)
\[\frac{{{a}^{4}}+{{b}^{4}}}{{{a}^{2}}{{b}^{2}}}\]
done
clear
D)
\[\frac{{{a}^{2}}+{{b}^{2}}}{ab}\]
done
clear
View Answer play_arrow
question_answer 191) In a \[\Delta \,ABC,\]\[a=8cm,\text{ }b=10cm\] and\[c=12cm\] The relation between angles of the triangle is
A)
\[C=A+B\]
done
clear
B)
\[C=2B\]
done
clear
C)
\[C=2A\]
done
clear
D)
\[C=3A\]
done
clear
View Answer play_arrow
question_answer 192) The area bounded by the curve \[y=1+{{\log }_{e}}\,\,x,\] the x-axis and the straight line x = e is equal to (in square units)
A)
\[3e-2\]
done
clear
B)
\[e\]
done
clear
C)
\[e-\frac{1}{e}\]
done
clear
D)
\[e+\frac{1}{e}\]
done
clear
View Answer play_arrow
question_answer 193) The general solution of the differential equation \[\frac{{{d}^{2}}y}{d{{x}^{2}}}={{e}^{2x}}+{{e}^{-x}}\] is
A)
\[4{{e}^{2x}}+{{e}^{-x}}+{{C}_{1}}x+{{C}_{2}}\]
done
clear
B)
\[\frac{1}{4}{{e}^{2x}}-{{e}^{-x}}+C\]
done
clear
C)
\[\frac{1}{4}{{e}^{2x}}+{{e}^{-x}}+{{C}_{1}}x+{{C}_{2}}\]
done
clear
D)
\[\frac{1}{4}{{e}^{2x}}-{{e}^{-x}}+{{C}_{1}}x+{{C}_{2}}\]
done
clear
View Answer play_arrow
question_answer 194) \[\int_{-3}^{2}{[f(x)+f(-x)]\,\,.\,\,[g(x)-g(-x)]\,\,dx}\] is equal to
A)
\[0\]
done
clear
B)
\[2\int_{-3}^{3}{f\,(x)dx}\]
done
clear
C)
\[2\int_{0}^{3}{f\,(x)\,\,g\,\,(x)\,\,dx}\]
done
clear
D)
\[2\int_{0}^{3}{[f(x)-g(x)]\,dx}\]
done
clear
View Answer play_arrow
question_answer 195) The degree of the differential equation \[\frac{{{d}^{2}}y}{d{{x}^{2}}}=\frac{5y+\frac{dy}{dx}}{\sqrt{\frac{{{d}^{2}}y}{d{{x}^{2}}}}}\]is equal to
A)
\[2\]
done
clear
B)
\[3\]
done
clear
C)
\[4\]
done
clear
D)
\[5/2\]
done
clear
View Answer play_arrow
question_answer 196) Three forces P, Q and R acting at a point 0 in the plane. The measure of \[\angle POQ\] and \[\angle QOR\] are \[{{120}^{o}}\] and \[{{90}^{o}}\] respectively. Then, the equilibrium forces P, Q and R are in the ratio
A)
\[3:1:2\]
done
clear
B)
\[2:1:3\]
done
clear
C)
\[\sqrt{3}:1:2\]
done
clear
D)
\[2:1:\sqrt{3}\]
done
clear
View Answer play_arrow
question_answer 197) The position vector of two given points A and B are \[4i-3j-k\]and \[5i-5j+k\]respectively. If y is the angle between AB and z-axis, then \[\cos \,\gamma \] is equal to
A)
\[1/3\]
done
clear
B)
\[2/3\]
done
clear
C)
\[-2/3\]
done
clear
D)
\[0\]
done
clear
View Answer play_arrow
question_answer 198) Let a, b and c be the unit vectors, such that \[b\,.\,c=a\,.\,c=0\]. If the angle between a and b is \[\pi /3\], then c equals to
A)
\[\pm \frac{2}{\sqrt{3}}\,(a\times b)\]
done
clear
B)
\[\pm \frac{\sqrt{3}}{2}\,(a\times b)\]
done
clear
C)
\[\pm \,2\,\,(a\times b)\]
done
clear
D)
\[\pm \,\,\frac{1}{2}\,(a\times b)\]
done
clear
View Answer play_arrow
question_answer 199) The sum of two vectors a and b is a vector c, such that \[|a|=|b|=|c|=2.\] Then, the magnitude of \[a-b\] is equal to
A)
\[\sqrt{3}\]
done
clear
B)
\[2\]
done
clear
C)
\[2\sqrt{3}\]
done
clear
D)
\[0\]
done
clear
View Answer play_arrow
question_answer 200) The vectors \[2i-j+k,\,\,i+2j-3k\]and \[3i+\lambda j+5k\] are coplanar, if \[\lambda \] equals to
A)
\[1\]
done
clear
B)
\[-1\]
done
clear
C)
\[-4\]
done
clear
D)
\[4\]
done
clear
View Answer play_arrow
question_answer 201) For the non-zero vectors a, b and c, the relation \[a.\,(b\times c)=0\] is true, if
A)
\[b\bot \,\,c\]
done
clear
B)
\[a\bot \,\,b\]
done
clear
C)
\[a||\,\,c\]
done
clear
D)
\[a\bot \,c\]
done
clear
View Answer play_arrow
question_answer 202) If \[{{S}_{1}},{{S}_{2}}\] and \[{{S}_{3}}\] are the sum of n, \[2n\]and \[3n\] terms respectively of an arithmetic progression, then
A)
\[{{S}_{3}}=2\,\,({{S}_{1}}+{{S}_{2}})\]
done
clear
B)
\[{{S}_{3}}={{S}_{1}}+{{S}_{2}}\]
done
clear
C)
\[{{S}_{3}}=3\,({{S}_{2}}-{{S}_{1}})\]
done
clear
D)
\[{{S}_{3}}=3\,({{S}_{2}}+{{S}_{1}})\]
done
clear
View Answer play_arrow
question_answer 203) The coefficient of \[{{p}^{n}}{{q}^{n}}\] in the expansion of \[{{[(1+p)\,\,(1+q)\,\,(p\,+q)]}^{n}}\] is
A)
\[\sum\limits_{k=0}^{n}{{{[C\,\,(n,\,\,k)]}^{2}}}\]
done
clear
B)
\[\sum\limits_{k=0}^{n}{{{[C\,\,(n,\,\,k+2)]}^{2}}}\]
done
clear
C)
\[\sum\limits_{k=0}^{n}{{{[C\,\,(n,\,\,k+3)]}^{2}}}\]
done
clear
D)
\[\sum\limits_{k=0}^{n3}{{{[C\,\,(n,\,\,k)]}^{2}}}\]
done
clear
View Answer play_arrow
question_answer 204) The number of even numbers of three digits which can be formed with digits \[0,1,\text{ }2,\text{ }3,4\] and 5 (no digit being used more than once) is
A)
\[60\]
done
clear
B)
\[92\]
done
clear
C)
\[52\]
done
clear
D)
\[48\]
done
clear
View Answer play_arrow
question_answer 205) If \[{{4}^{x}}={{16}^{y}}={{64}^{z}},\]then
A)
\[x,\text{ }y,\text{ }z\]are in GP
done
clear
B)
\[x,\text{ }y,\text{ }z\]are in AP
done
clear
C)
\[\frac{1}{x},\frac{1}{y},\frac{1}{z}\] tare in GP
done
clear
D)
\[\frac{1}{x},\frac{1}{y},\frac{1}{z}\] are in AP
done
clear
View Answer play_arrow
question_answer 206) The constant terms is the expansion of \[{{\left( \sqrt{x}-\frac{c}{{{x}^{2}}} \right)}^{10}}\]is \[180,\]then the value of c equals to
A)
\[\pm \,\,2\]
done
clear
B)
\[\pm \,\,3\]
done
clear
C)
\[\pm \,\,4\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 207) A student is allowed to select at best n books from a collection of \[(2n\,+1)\] books. If the total number of ways in which he can select a book is 255, then the value of n equals to
A)
\[6\]
done
clear
B)
\[5\]
done
clear
C)
\[4\]
done
clear
D)
\[3\]
done
clear
View Answer play_arrow
question_answer 208) If \[f(x)=\frac{1}{2-x},\] then \[f\,\,(f(x))\] is discontinous at
A)
\[x=2,4\]
done
clear
B)
\[x=4,\,3/2\]
done
clear
C)
\[x=2,3/2\]
done
clear
D)
\[x=4\]
done
clear
View Answer play_arrow
question_answer 209) If \[g(x)\] is the inverse of \[f(x)\] and \[f'(x)=\cos x,\] then \[g'(x)\] is equal to
A)
\[\sec \,\,x\]
done
clear
B)
\[\sec \,\,(g\,\,(x))\]
done
clear
C)
\[\cos \,(g\,(x))\]
done
clear
D)
\[-\sin \,\,(g\,(x)\,)\]
done
clear
View Answer play_arrow
question_answer 210) The derivative of \[\text{cose}{{\text{c}}^{-1}},\,\,\,\,\left( \frac{1}{2x\,\sqrt{1-{{x}^{2}}}} \right)\] with respect to \[\sqrt{1-{{x}^{2}}}\] is
A)
\[\frac{1}{\sqrt{1-{{x}^{2}}}}\]
done
clear
B)
\[\frac{2}{x}\]
done
clear
C)
\[-\frac{2}{x}\]
done
clear
D)
\[\frac{-1}{\sqrt{1-{{x}^{2}}}}\]
done
clear
View Answer play_arrow
question_answer 211) If \[f(x)=|x-2|\,{{\log }_{10}}\,(x-1),\] then \[f\] is differentiable in
A)
\[R-\{\,1,\,\,\,11\}\]
done
clear
B)
\[R-\{\,2,\,\,\,11\}\]
done
clear
C)
\[R-\{\,11\}\]
done
clear
D)
\[R-\{\,1,\,\,2\}\]
done
clear
View Answer play_arrow
question_answer 212) If \[x\ne 0\] and \[y={{\log }_{e}}\,|2x|,\] then \[\frac{dy}{dx}\] is equal to
A)
\[\frac{1}{x}\]
done
clear
B)
\[-\frac{1}{x}\]
done
clear
C)
\[\pm \,\frac{1}{2x}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 213) The curves \[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{2}=1\] and \[{{y}^{2}}=8x\]intersect at right angles, if \[{{a}^{2}}\]is equal to
A)
\[1/2\]
done
clear
B)
\[1\]
done
clear
C)
\[2\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 214) The plane \[2x-2y+z+5=0\] is a tangent to the sphere \[{{(x-2)}^{2}}+{{(y-2)}^{2}}+{{(z-1)}^{2}}={{r}^{2}},\] if r equals
A)
\[1\]
done
clear
B)
\[2\]
done
clear
C)
\[4\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 215) A bag has four pair of balls of four distinct colours. If four balls are picked at random (without replacement), the probability that there is atleast one pair among them have the same colour is
A)
\[\frac{1}{7\,\,!}\]
done
clear
B)
\[\frac{8}{35}\]
done
clear
C)
\[\frac{19}{35}\]
done
clear
D)
\[\frac{27}{35}\]
done
clear
View Answer play_arrow
question_answer 216) Suppose \[f(x)=\frac{k}{{{2}^{x}}}\] is a probability distribution of a random variable X that can take on the values \[x=0,1,\text{ }2,\text{ }3,\text{ }4\]. Then, k is equal to
A)
\[\frac{16}{15}\]
done
clear
B)
\[\frac{15}{16}\]
done
clear
C)
\[\frac{31}{16}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 217) The contrapositive statement of the proposition \[p\to \tilde{\ }q\] is
A)
\[\tilde{\ }p\to q\]
done
clear
B)
\[\tilde{\ }q\to p\]
done
clear
C)
\[q\to \tilde{\ }p\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 218) If A and B are mutually exclusive events, such that \[P(A)=0.25,\,\,\,\,\,\,P(B)=0.4,\] then \[P({{A}^{c}}\,\cap {{B}^{c}})\]is equal to
A)
\[0.45\]
done
clear
B)
\[0.55\]
done
clear
C)
\[0.9\]
done
clear
D)
\[0.35\]
done
clear
View Answer play_arrow
question_answer 219) Let \[f(x)=\frac{3}{1+{{3}^{\tan \,x}}}\]. Then, which of the following is true?
A)
\[\underset{x\to \frac{{{\pi }^{-}}}{2}}{\mathop{\lim }}\,\,\,f(x)\,=3\]
done
clear
B)
\[\underset{x\to \frac{{{\pi }^{+}}}{2}}{\mathop{\lim }}\,\,\,f(x)\,=0\]
done
clear
C)
\[\underset{x\to \frac{{{\pi }^{+}}}{2}}{\mathop{\lim }}\,\,\,f(x)\,=3\]
done
clear
D)
\[\underset{x\to \frac{\pi }{2}}{\mathop{\lim }}\,\,\,f(x)\] exists
done
clear
View Answer play_arrow
question_answer 220) The general solution of \[\cos \,x\,.\,\cos \,6x=-1\]is
A)
\[x=(2n+1)\frac{\pi }{7},\,n\in Z\]
done
clear
B)
\[x=(2n+1)\frac{\pi }{5},\,n\in Z\]
done
clear
C)
\[x=(2n+1)\frac{\pi }{35},\,n\in Z\]
done
clear
D)
\[x=(2n+1)\,\pi ,\,n\in Z\]
done
clear
View Answer play_arrow
question_answer 221) The value of \[\tan \left[ {{\cos }^{-1}}\left( \frac{3}{5} \right)+{{\tan }^{-1}}\left( \frac{2}{3} \right) \right]\] is
A)
\[6\]
done
clear
B)
\[17/6\]
done
clear
C)
\[6/17\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 222) If A is a square matrix of order 3 and a is a real number, then determinant \[|\alpha \,\,\,A|\] is equal to
A)
\[{{\alpha }^{2}}\,|\,\,A|\]
done
clear
B)
\[\alpha \,|\,\,A|\]
done
clear
C)
\[{{\alpha }^{3}}\,|\,\,A|\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 223) The number of solution of the equation \[\sin x+\sin 5x=\sin 3x\] tying in the interval \[[0,\,\pi ]\] is
A)
\[4\]
done
clear
B)
\[6\]
done
clear
C)
\[5\]
done
clear
D)
\[2\]
done
clear
View Answer play_arrow
question_answer 224) The ' value of \[\sin \,\left[ {{\tan }^{-1}}\,\,\left( \frac{1-{{x}^{2}}}{2x} \right)+{{\cos }^{-1}}\left( \frac{1-{{x}^{2}}}{1+{{x}^{2}}} \right) \right]\] is
A)
\[1\]
done
clear
B)
\[0\]
done
clear
C)
\[-1\]
done
clear
D)
\[\frac{\pi }{2}\]
done
clear
View Answer play_arrow
question_answer 225) The system of equations \[2x-y+z=0,\]\[ax-y+2z=0\]and \[x-2y+z=0\] has non-zero solution, if a is equal to
A)
\[1\]
done
clear
B)
\[2\]
done
clear
C)
\[4\]
done
clear
D)
\[5\]
done
clear
View Answer play_arrow