question_answer 1) Vector which is perpendicular to \[a\,\,\cos \,\theta \,\,\hat{i}+b\,\sin \,\theta \,\,\hat{j}\] is
A)
\[b\,\sin \,\theta \,\hat{i}-a\,\cos \,\theta \,\hat{j}\]
done
clear
B)
\[\frac{1}{a}\,\sin \,\theta \,\hat{i}-a\,\cos \,\theta \,\hat{j}\]
done
clear
C)
\[5\hat{k}\]
done
clear
D)
All of the above
done
clear
View Answer play_arrow
question_answer 2) Which of the following statements is true?
A)
When the coordinate axes are translated the component of a vector in a plane changes
done
clear
B)
When the coordinate axes are rotated through some angle components of the vector change but the vector's magnitude remains constant
done
clear
C)
Sum of \[\vec{a}\]and \[\vec{b}\] is \[\vec{R}\]. If the magnitude of \[\vec{a}\]alone is increased angle between \[\vec{b}\] and \[\vec{R}\] decreases
done
clear
D)
The cross product of \[3\,\,\hat{i}\] and \[4\,\,\hat{j}\] is 12
done
clear
View Answer play_arrow
question_answer 3) From a balloon rising vertically upwards as \[5\text{ }m/s\]a stone is thrown up at 10 m/s relative to the balloon. Its velocity with respect to ground after \[2\text{ }s\]is (assume\[g=10\text{ }m/{{s}^{2}}\])
A)
zero
done
clear
B)
\[5\text{ }m/s\]
done
clear
C)
\[10\text{ }m/s\]
done
clear
D)
\[20\text{ }m/s\]
done
clear
View Answer play_arrow
question_answer 4) Two bodies are projected from ground with equal speed \[20\text{ }m/s\]from the same position in the same vertical plane to have equal range but at different angles above the horizontal. If one of the angle is 30° the sum of their maximum heights is (assume\[g=10\text{ }m/{{s}^{2}}\])
A)
\[400\,\,m\]
done
clear
B)
\[20\,\,m\]
done
clear
C)
\[30\,\,m\]
done
clear
D)
\[40\,\,m\]
done
clear
View Answer play_arrow
question_answer 5) Which of the following quantities measured from different inertial reference frames are same?
A)
Force
done
clear
B)
Velocity
done
clear
C)
Displacement
done
clear
D)
Kinetic energy
done
clear
View Answer play_arrow
question_answer 6) Two particles of equal mass are connected to a rope AB of negligible mass, such that one is at end A and the other dividing the length of the rope in the ratio \[1:2\] from B. The rope is rotated about end B in a horizontal plane. Ratio of the tensions in the smaller part to the other is (ignore effect of gravity)
A)
\[4:3\]
done
clear
B)
\[1:4\]
done
clear
C)
\[1:2\]
done
clear
D)
\[1:3\]
done
clear
View Answer play_arrow
question_answer 7) Angle of banking for a vehicle speed of \[10\text{ }m/s\] for a radius of curvature \[10\text{ }m\]is (assume\[g=10\text{ }m/{{s}^{2}}\])
A)
\[{{30}^{o}}\]
done
clear
B)
\[{{\tan }^{-1}}\left( \frac{1}{2} \right)\]
done
clear
C)
\[{{60}^{o}}\]
done
clear
D)
\[{{45}^{o}}\]
done
clear
View Answer play_arrow
question_answer 8) A body of mass \[2\text{ }kg\]is projected at \[20\text{ }m/s\]at an angle \[{{60}^{o}}\] above the horizontal. Power due to the gravitational force at its highest point is
A)
\[200\text{ }W\]
done
clear
B)
\[100\sqrt{3\,}W\]
done
clear
C)
\[50\,W\]
done
clear
D)
zero
done
clear
View Answer play_arrow
question_answer 9) A block of mass \[2\text{ }kg\]rests on a horizontal surface. If a horizontal force of \[5\text{ }N\]is applied on the block the frictional force on, it is \[({{\mu }_{k}}=0.4,\,\,{{\mu }_{s}}=0.5)\]
A)
\[5\,\,N\]
done
clear
B)
\[10\,\,N\]
done
clear
C)
\[8\,\,N\]
done
clear
D)
zero
done
clear
View Answer play_arrow
question_answer 10) Three idential spheresof mass M each are placed at the comers of an equilateral triangle of side \[2m\]. Taking one of the comer as the origin, the position vector of the centre of mass is
A)
\[\sqrt{3}\,\,(\hat{i}-\hat{j})\]
done
clear
B)
\[\frac{i}{\sqrt{3}}+\hat{j}\]
done
clear
C)
\[\frac{\hat{i}+\hat{j}}{3}\]
done
clear
D)
\[\hat{i}+\frac{{\hat{j}}}{\sqrt{3}}\]
done
clear
View Answer play_arrow
question_answer 11) A shell initially at rest explodes into two pieces of equal mass, the two pieces will
A)
move with different velocities in different Directions
done
clear
B)
move with the same velocity in opposite directions
done
clear
C)
move with the same velocity in the same direction
done
clear
D)
be at rest
done
clear
View Answer play_arrow
question_answer 12) Impulse is
A)
a scalar
done
clear
B)
equal to change in the momentum of a body
done
clear
C)
equal to rate of change of momentum of a body
done
clear
D)
a force
done
clear
View Answer play_arrow
question_answer 13) In a head on elastic collision of a very heavy body moving at V with a light body at rest, velocity of heavy body after collision is
A)
\[V\]
done
clear
B)
\[2\,V\]
done
clear
C)
zero
done
clear
D)
\[\frac{V}{2}\]
done
clear
View Answer play_arrow
question_answer 14)
A T Joint is formed by two identical rods A and B each of mass m and length L in the XY plane as shown. Its moment of inertia about axis coinciding with A is
A)
\[\frac{2\,m{{L}^{2}}}{3}\]
done
clear
B)
\[\frac{\,m{{L}^{2}}}{12}\]
done
clear
C)
\[\frac{\,m{{L}^{2}}}{6}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 15) A disc of moment of inertia \[5\text{ }kg-{{m}^{2}}\]is acted upon by a constant torque of\[40\text{ }Nm\]. Starting from rest the time taken by it to acquire an angular velocity of 24 rad/s is
A)
\[3\text{ }s\]
done
clear
B)
\[\text{4 }s\]
done
clear
C)
\[2.5\,\,s\]
done
clear
D)
\[120\,\,s\]
done
clear
View Answer play_arrow
question_answer 16) If the angular momentum of a rotating body about a fixed axis is increased by\[10%\]. Its kinetic energy will be increased by
A)
\[10%\]
done
clear
B)
\[20%\]
done
clear
C)
\[21%\]
done
clear
D)
\[5%\]
done
clear
View Answer play_arrow
question_answer 17) If the earth were to spin faster, acceleration due to gravity at the poles
A)
increases
done
clear
B)
decreases
done
clear
C)
remains the same
done
clear
D)
depends on how fast it spins
done
clear
View Answer play_arrow
question_answer 18) The time period of an artificial satellite in a circular orbit is independent of
A)
the mass of the satellite
done
clear
B)
radius of the orbit
done
clear
C)
mass of the earth and radius of the earth
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 19) Angle of contact of a liquid with a solid depends on
A)
solid only
done
clear
B)
liquid only
done
clear
C)
both on solid and liquid
done
clear
D)
orientation of the solid surface in liquid
done
clear
View Answer play_arrow
question_answer 20) If longitudinal strain for a wire is \[0.03\] and its Poisson's ratio is \[0.5,\] then its lateral strain is
A)
\[0.003\]
done
clear
B)
\[0.0075\]
done
clear
C)
\[0.015\]
done
clear
D)
\[0.4\]
done
clear
View Answer play_arrow
question_answer 21) When the temperature increases, the viscosity of
A)
gas decreases and liquid increases
done
clear
B)
gas increases and liquid decreases
done
clear
C)
gas and liquid increases
done
clear
D)
gas and liquid decreases
done
clear
View Answer play_arrow
question_answer 22) Water flows steadily through a horizontal pipe of variable cross-section. If the pressure of water is p at a point where flow speed is v, the pressure at another point where the flow of speed is \[2\text{ }v,\]is (take density of water as p)
A)
\[p-\frac{3\,\rho {{v}^{2}}}{2}\]
done
clear
B)
\[p-\frac{\,\rho {{v}^{2}}}{2}\]
done
clear
C)
\[p-\frac{3\,\rho {{v}^{2}}}{4}\]
done
clear
D)
\[p-\rho {{v}^{2}}\]
done
clear
View Answer play_arrow
question_answer 23) Which of the following statements is true?
A)
Internal energy of a gas depends only on the state of the gas
done
clear
B)
In an isothermal process change in internal energy is maximum
done
clear
C)
Area under pressure, volume graph equals heat supplied in any process
done
clear
D)
Work done is state dependent but not path dependent
done
clear
View Answer play_arrow
question_answer 24) A gas \[\left( \gamma =\frac{5}{3} \right),\] expands isobaric ally. The percentage, of heat supplied that increases thermal energy and that involved in doing work for expansion is
A)
\[40:60\]
done
clear
B)
\[60:40\]
done
clear
C)
\[50:50\]
done
clear
D)
\[25:30\]
done
clear
View Answer play_arrow
question_answer 25) A perfect black body is one whose emissive power is
A)
maximum
done
clear
B)
zero
done
clear
C)
unity
done
clear
D)
minimum
done
clear
View Answer play_arrow
question_answer 26) A black body at a temperature T radiates energy at E. If the temperature falls to \[\frac{T}{2},\] the radiated energy will be
A)
\[\frac{E}{4}\]
done
clear
B)
\[\frac{E}{2}\]
done
clear
C)
\[2E\]
done
clear
D)
\[\frac{E}{16}\]
done
clear
View Answer play_arrow
question_answer 27) If the units of mass, length and time are doubled unit of angular momentum will be .
A)
doubled
done
clear
B)
tripled
done
clear
C)
quadrupled
done
clear
D)
8 times the original value
done
clear
View Answer play_arrow
question_answer 28) Which of the following graphs shows variation of potential energy (U) with position x?
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Answer play_arrow
question_answer 29) Choose the correct statement
A)
Time period of a simple pendulum depends on amplitude
done
clear
B)
Time shown by a spring watch varies with acceleration due to gravity
done
clear
C)
In a simple pendulum time period varies linearly with the length of the pendulum
done
clear
D)
The graph between length of the pendulum and time period is a parabola
done
clear
View Answer play_arrow
question_answer 30) Time period of a spring mass system is T. If this spring is cut into two parts whose lengths are in the ratio \[1:3\] and the same mass is attached to the longer part, the new time period will be
A)
\[\sqrt{\frac{3}{2}}T\]
done
clear
B)
\[\frac{T}{\sqrt{3}}\]
done
clear
C)
\[\frac{\sqrt{3}T}{2}\]
done
clear
D)
\[\sqrt{3}T\]
done
clear
View Answer play_arrow
question_answer 31) Equation of progressive wave is \[y=A\,\sin \left( 10\,\pi x+11\pi t+\frac{\pi }{3} \right)\]
A)
its wavelength is \[2\text{ }units\]
done
clear
B)
it is travelling in the positive x-direction
done
clear
C)
wave velocity is \[1.5\text{ }units\]
done
clear
D)
time period of SHM is 1 s
done
clear
View Answer play_arrow
question_answer 32) The phenomenon of sound propagation in air is
A)
isothermal process
done
clear
B)
isobaric process
done
clear
C)
adiabatic process
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 33) The second overtone of an open pipe is in resonance with the first overtone of a closed pipe of length \[2\,m\]. Length of the open pipe is
A)
\[4\,m\]
done
clear
B)
\[2\,m\]
done
clear
C)
\[8\,m\]
done
clear
D)
\[1\,m\]
done
clear
View Answer play_arrow
question_answer 34) Choose the correct statement
A)
Beats are due to destructive interference
done
clear
B)
Maximum beat frequency audible to a human being is 20
done
clear
C)
Beats are as a result of Doppler?s effect
done
clear
D)
Beats are due to superposition of two waves of nearly equal frequencies
done
clear
View Answer play_arrow
question_answer 35) A motor car is approaching towards a crossing with a velocity of\[72\text{ }km/h\]. The frequency of sound of its horn as heard by a policeman standing on the crossing is\[260\text{ }Hz\]. The frequency of horn is
A)
\[200\text{ }Hz\]
done
clear
B)
\[244\text{ }Hz\]
done
clear
C)
\[150\text{ }Hz\]
done
clear
D)
\[80\text{ }Hz\]
done
clear
View Answer play_arrow
question_answer 36) Forces exerted by a uniform electric field on an electron having mass \[{{m}_{e}}\] and proton of mass \[{{m}_{p}}\]are represented as \[{{F}_{e}}\] and \[{{F}_{p}}\] respectively are related as
A)
\[{{F}_{p}}={{F}_{e}}\]
done
clear
B)
\[\frac{{{F}_{e}}}{{{F}_{p}}}=\frac{{{m}_{e}}}{{{m}_{p}}}\]
done
clear
C)
\[\frac{{{F}_{e}}}{{{F}_{p}}}=\frac{{{m}_{p}}}{{{m}_{e}}}\]
done
clear
D)
\[\frac{{{F}_{e}}}{{{F}_{p}}}=\frac{m_{e}^{2}}{m_{p}^{2}}\]
done
clear
View Answer play_arrow
question_answer 37) Electric field strength due to a dipole at a point on the axial line of dipole is
A)
from positive charge to negative charge
done
clear
B)
from negative charge to positive charge
done
clear
C)
along the equatorial line
done
clear
D)
at an angle to axial line
done
clear
View Answer play_arrow
question_answer 38) Potential and field strength at a certain distance from a point charge are \[600\text{ }V\]and\[200\text{ }N/C\]. Distance of the point from the charge is
A)
\[2\,m\]
done
clear
B)
\[4\,m\]
done
clear
C)
\[8\,m\]
done
clear
D)
\[3\,m\]
done
clear
View Answer play_arrow
question_answer 39) Two identical spheres with charges \[4q,-2q\] kept some distance apart exert a force F on each other. If they are made to touch each other and replaced at their old positions, the force between them will be
A)
\[\frac{1}{9}F\]
done
clear
B)
\[\frac{1}{8}F\]
done
clear
C)
\[\frac{9}{8}F\]
done
clear
D)
\[\frac{8}{9}F\]
done
clear
View Answer play_arrow
question_answer 40) Two capacitors each of capacity \[2\mu F\] are connected in parallel. If they are connected to \[100\text{ }V\]battery, then energy stored in them is
A)
\[0.02\text{ }J\]
done
clear
B)
\[0.04\text{ }J\]
done
clear
C)
\[0.01\text{ }J\]
done
clear
D)
\[200\text{ }J\]
done
clear
View Answer play_arrow
question_answer 41) Which factor is immaterial for the wire used in electric fuse?
A)
Length
done
clear
B)
Radius
done
clear
C)
Material
done
clear
D)
Current
done
clear
View Answer play_arrow
question_answer 42) A battery of emf \[2\text{ }V\]and internal resistance \[0.1\Omega \] is being charged by a current of \[~5\text{ }A\]. The potential difference between the terminals of the battery is
A)
\[2.5\text{ }V\]
done
clear
B)
\[1.5\text{ }V\]
done
clear
C)
\[0.5V\]
done
clear
D)
\[1\,\,V\]
done
clear
View Answer play_arrow
question_answer 43) An electric bulb is rated at \[220\text{ }V,\] \[200\text{ }W;\] Power consumed by it when operated at \[110\text{ }V\]is
A)
\[25\text{ }W\]
done
clear
B)
\[50\text{ }W\]
done
clear
C)
\[75\text{ }W\]
done
clear
D)
\[90\text{ }W\]
done
clear
View Answer play_arrow
question_answer 44)
two cells having emf \[4\text{ }V,\] \[2\text{ }V\]and internal resistances \[1\,\Omega ,\] \[1\,\,\Omega \] are connected as shown in figure below. Current through \[6\,\,\Omega \] resistance is
A)
\[\frac{1}{3}A\]
done
clear
B)
\[\frac{2}{3}A\]
done
clear
C)
\[1\,\,A\]
done
clear
D)
\[\frac{2}{9}\,\,A\]
done
clear
View Answer play_arrow
question_answer 45) For a given thermocouple neutral temperature
A)
is a constant
done
clear
B)
depends on cold junction temperature
done
clear
C)
depends on inversion temperature
done
clear
D)
double that of cold junction temperature
done
clear
View Answer play_arrow
question_answer 46) A charged particle enters a uniform magnetic field with a certain speed at right angles to it. In the magnetic field a change could occur in its
A)
kinetic energy
done
clear
B)
angular momentum
done
clear
C)
linear momentum
done
clear
D)
speed
done
clear
View Answer play_arrow
question_answer 47) A coil having 500 turns of square shape each of side \[10\text{ }cm\]is placed normal to a magnetic field which is increasing at \[1\text{ }T/s\]. The induced emf is
A)
\[0.1\text{ }V\]
done
clear
B)
\[0.5\,\,V\]
done
clear
C)
\[1\,\,V\]
done
clear
D)
\[-5\,\,V\]
done
clear
View Answer play_arrow
question_answer 48) A galvanometer has a resistance \[50\,\,\Omega \]. A resistance of \[5\,\,\Omega \] is connected parallel to it. Fraction of the total current flowing through galvanometer is
A)
\[\frac{1}{10}\]
done
clear
B)
\[\frac{1}{11}\]
done
clear
C)
\[\frac{1}{50}\]
done
clear
D)
\[\frac{2}{15}\]
done
clear
View Answer play_arrow
question_answer 49) A wire oriented in the east-west direction carries a current eastward. Direction of the magnetic field at a point to the south of the wire is
A)
vertically down
done
clear
B)
vertically up
done
clear
C)
north-east
done
clear
D)
south-east
done
clear
View Answer play_arrow
question_answer 50) An inductor is connected to an AC source, When compared to voltage, the current in the lead wires
A)
is ahead in phase by n
done
clear
B)
lags in phase by n
done
clear
C)
is ahead in phase by ?
done
clear
D)
lags in phase by ?
done
clear
View Answer play_arrow
question_answer 51) Curie temperature is the one above which
A)
paramagnetic substance changes to ferromagnetic
done
clear
B)
paramagnetic changes to diamagnetic
done
clear
C)
diamagnetic changes to paramagnetic
done
clear
D)
ferromagnetic changes to paramagnetic
done
clear
View Answer play_arrow
question_answer 52) Energy in a current carrying coil is stored in the form of
A)
electric field
done
clear
B)
magnetic field
done
clear
C)
heat
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 53) Graph of force per unit length between two long parallel currents carrying conductor and the distance between them is
A)
straight line
done
clear
B)
parabola
done
clear
C)
ellipse
done
clear
D)
rectangular hyperbola
done
clear
View Answer play_arrow
question_answer 54) A bar magnet is held at right angles to a uniform magnetic field. The couple acting on the magnet is to be halved by rotating it from this position. The angle of rotation is
A)
\[{{60}^{o}}\]
done
clear
B)
\[{{45}^{o}}\]
done
clear
C)
\[{{30}^{o}}\]
done
clear
D)
\[{{75}^{o}}\]
done
clear
View Answer play_arrow
question_answer 55) A point source of light is kept below the surface of water in a pond
A)
light emerges from every point of the surface of the pond
done
clear
B)
no light is transmitted from the surface of the pond
done
clear
C)
all the light emitted by the source emerges from a circular region of the pond
done
clear
D)
some of the light emitted by the source emerges from a circular region of the pond
done
clear
View Answer play_arrow
question_answer 56) If white light is used in Young's double slit experiment
A)
no interference pattern is formed
done
clear
B)
white fringes are formed
done
clear
C)
central bright fringe is white
done
clear
D)
central bright fringe is coloured
done
clear
View Answer play_arrow
question_answer 57) Electromagnetic waves can be deflected by
A)
electric fields only
done
clear
B)
magnetic fields only
done
clear
C)
Both [a] and [b]
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 58) Maximum lateral displacement of a ray of light incident on a slab of thickness t is
A)
\[\frac{t}{2}\]
done
clear
B)
\[\frac{t}{3}\]
done
clear
C)
\[\frac{t}{4}\]
done
clear
D)
\[t\]
done
clear
View Answer play_arrow
question_answer 59) Mercury vapour lamp gives
A)
continuous spectrum
done
clear
B)
line spectrum
done
clear
C)
band spectrum
done
clear
D)
absorption spectrum
done
clear
View Answer play_arrow
question_answer 60) Pick the correct statement from the following
A)
Primary rainbow is a virtual image and secondary rainbow is a real image
done
clear
B)
Primary rainbow is a real image and secondary rainbow is a virtual image
done
clear
C)
Both primary and secondary rainbows are virtual images
done
clear
D)
Both primary and secondary rainbows are real images
done
clear
View Answer play_arrow
question_answer 61) The refractive index of water, glass and diamond are \[1.33,1.50,\text{ }2.40\]respectively. The refractive index of diamond relative to water and of glass relative to diamond, respectively are nearly
A)
\[1.80,0.625\]
done
clear
B)
\[0.554,\text{ }0.625\]
done
clear
C)
\[1.80,\text{ }1.6\]
done
clear
D)
\[0.554,\text{ }1.6\]
done
clear
View Answer play_arrow
question_answer 62) In the diffraction pattern of a single slit
A)
all bands are uniformly bright
done
clear
B)
all bands are uniformly wide
done
clear
C)
central band is narrower
done
clear
D)
central band is wider
done
clear
View Answer play_arrow
question_answer 63) A radioactive substance has a half-life of four months. Three-fourth of the substance will decay in
A)
\[3\text{ }months\]
done
clear
B)
\[4\text{ }months\]
done
clear
C)
\[~8\text{ }months\]
done
clear
D)
\[\text{12 }months\]
done
clear
View Answer play_arrow
question_answer 64) Electrons in the atom are held to the nucleus by
A)
Coulomb's forces
done
clear
B)
nuclear forces
done
clear
C)
van der Waals' forces
done
clear
D)
gravitational forces
done
clear
View Answer play_arrow
question_answer 65) Mass of the nucleons together in a heavy nucleus is
A)
greater than mass of nucleus
done
clear
B)
equal to mass of nucleus
done
clear
C)
same as mass of nucleus
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 66) Ratio of the radii of the nuclei with mass numbers 8 and 27 would be
A)
\[27/8\]
done
clear
B)
\[8/27\]
done
clear
C)
\[2/3\]
done
clear
D)
\[3/2\]
done
clear
View Answer play_arrow
question_answer 67) Stopping potential required to reduce the photoelectric current to zero
A)
is directly proportional to the wavelength of the incident radiation
done
clear
B)
increases uniformly with wavelength of the incident radiation
done
clear
C)
is directly proportional to the frequency of the incident radiation
done
clear
D)
decreases uniformly with the frequency of the incident radiation
done
clear
View Answer play_arrow
question_answer 68) The first member of the Ballmer?s series of the hydrogen has a wavelength \[\lambda ,\] the wavelength of the second member of its series is
A)
\[\frac{27}{20}\lambda \]
done
clear
B)
\[\frac{20}{27}\lambda \]
done
clear
C)
\[\frac{27}{20}\lambda \]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 69) The photoelectric threshold frequency of a metal is v. When light of frequency \[4v\] is incident on the metal. The maximum kinetic energy of the emitted photoelectrons is
A)
\[4\,\,hv\]
done
clear
B)
\[3\,\,hv\]
done
clear
C)
\[5\,\,hv\]
done
clear
D)
\[\frac{5}{2}\,\,hv\]
done
clear
View Answer play_arrow
question_answer 70) The shortest wavelength in Lyman series is\[91.2\text{ }nm\]. The longest wavelength of the series is
A)
\[121.6\text{ }nm\]
done
clear
B)
\[182.4\text{ }nm\]
done
clear
C)
\[243.4\text{ }nm\]
done
clear
D)
\[364.8\text{ }nm\]
done
clear
View Answer play_arrow
question_answer 71) Energy gap of a semiconductor is of the order of
A)
\[1\,\,eV\]
done
clear
B)
\[10\,\,eV\]
done
clear
C)
\[0.1\text{ }eV\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 72) Majority charge carriers in p-type material are
A)
holes
done
clear
B)
electrons
done
clear
C)
Both and
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 73) Resistance of a semiconductor
A)
increases with increase in temperature
done
clear
B)
decreases with increase in temperature
done
clear
C)
is not affected by change in temperature
done
clear
D)
increases for germanium and decreases for silicon
done
clear
View Answer play_arrow
question_answer 74) Semiconductor material having fewer free electrons than pure germanium or silicon is
A)
p-type
done
clear
B)
n-type
done
clear
C)
Both [a] and [b]
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 75) The concentrations of impurities in a transistor are
A)
equal for the emitter, base and collector regions
done
clear
B)
least for the emitter region
done
clear
C)
largest for the emitter region
done
clear
D)
least for the base region
done
clear
View Answer play_arrow
question_answer 76) At \[\text{25}{{\,}^{\text{o}}}\text{C}\], the total pressure of an ideal solution obtained by mixing 3 moles of 'A? and 2 moles of 'B? is 184 Ton". What is the vapour pressure (in Torr) of pure 'B' at the same temperature? (vapour pressure of pure 'A? at \[25{{\,}^{o}}C,\] is 200 Torr)
A)
180
done
clear
B)
160
done
clear
C)
16
done
clear
D)
100
done
clear
View Answer play_arrow
question_answer 77) Relative lowering of vapour pressure of a dilute solution is 0.2. What is the mole fraction of the non-volatile solute?
A)
0.8
done
clear
B)
0.5
done
clear
C)
0.3
done
clear
D)
0.2
done
clear
View Answer play_arrow
question_answer 78) Match the following List ?A? List ?B? (1) \[PhC{{O}_{2}}C{{H}_{3}}\] [A]\[2,4-\text{DNP}\] (2) \[{{C}_{6}}{{H}_{5}}C{{H}_{2}}C{{O}_{2}}H\] [B] Arndt-Eistert synthesis (3)\[{{C}_{6}}{{H}_{5}}CHO\] [C] Hydrolysis Correct answer is
A)
\[1-A,\,2-B,\,3-C\]
done
clear
B)
\[1-B,\,2-C,\,3-A\]
done
clear
C)
\[1-C,\,2-B,\,3-A\]
done
clear
D)
\[1-B,\,2-A,\,3-C\]
done
clear
View Answer play_arrow
question_answer 79) 2-pentanone and 3-methyl-2-butanone are a pair of....... isomers.
A)
functional
done
clear
B)
chain
done
clear
C)
positional
done
clear
D)
stereo
done
clear
View Answer play_arrow
question_answer 80) What are the units of entropy?
A)
\[\text{cal K}\]
done
clear
B)
\[\text{Cal}\,{{\text{K}}^{-1}}\]
done
clear
C)
\[\text{cm}\,{{\text{K}}^{-1}}\]
done
clear
D)
\[\text{ }\!\!~\!\!\text{ cmK}\]
done
clear
View Answer play_arrow
question_answer 81) Calculate \[\Delta H\](in Joules) for, C (graphite) \[\to C\](diamond), from the following data C(graphite)\[+\,{{O}_{2}}(g)\to C{{O}_{2}}(g);\] \[\Delta H=-393.5\,kJ\] C (diamond)\[+\,{{O}_{2}}(g)\to C{{O}_{2}}(g);\] \[\Delta H=-395.4\,kJ\]
A)
\[1,900\]
done
clear
B)
\[~-788.9\times {{10}^{3}}\]
done
clear
C)
\[1,90,000\]
done
clear
D)
\[~+\,788.9\times \,{{10}^{3}}\]
done
clear
View Answer play_arrow
question_answer 82) \[C{{H}_{2}}Br+\bar{O}H\xrightarrow{{}}C{{H}_{3}}OH+B{{r}^{-}}\]reaction proceeds by\[{{S}_{N}}2-\]mechanism. Its rate is dependent on the concentration of
A)
\[C{{H}_{3}}Br,\bar{O}H\]
done
clear
B)
\[C{{H}_{3}}Br\]only
done
clear
C)
\[~\bar{O}H\] only
done
clear
D)
\[~C{{H}_{3}}Br,C{{H}_{3}}OH\]
done
clear
View Answer play_arrow
question_answer 83) The end products in the Cannizaro reaction of benzaldehyde is
A)
\[~PhC{{O}_{2}}H,PhC{{H}_{2}}OH\]
done
clear
B)
\[~PhC{{O}_{2}}H,PhC{{H}_{2}}C{{O}_{2}}H\]
done
clear
C)
\[PhC{{H}_{2}}OH,PhCOC{{H}_{3}}\]
done
clear
D)
\[PhCO{{}_{2}}H,PhCOC{{H}_{3}}\]
done
clear
View Answer play_arrow
question_answer 84) For a chemicalreaction, the free energy change \[(\Delta G)\] is negative. The reaction is
A)
a spontaneous reaction
done
clear
B)
an equilibrium reaction
done
clear
C)
a non-spontaneous reaction
done
clear
D)
characterised by\[{{r}_{f}}-{{r}_{b}}\] (where\[{{r}_{f}}\]and\[{{r}_{b}}\] are rates of forward and backward reactions respectively)
done
clear
View Answer play_arrow
question_answer 85) In which of the following reactions, the heat liberated is known as "heat of combustion"?
A)
\[{{H}^{+}}(aq)+O{{H}^{-}}(aq)\to {{H}_{2}}O(l)+heat\]
done
clear
B)
\[C\text{(graphite)}+\frac{1}{2}{{O}_{2}}(g)\to CO(g)+\text{heat}\]
done
clear
C)
\[C{{H}_{4}}(g)+2{{O}_{2}}(g)\to C{{O}_{2}}(g)+2{{H}_{2}}O(l)+\,heat\]
done
clear
D)
\[{{H}_{2}}S{{O}_{4}}(aq)+{{H}_{2}}O(l)\to {{H}_{2}}S{{O}_{4}}(aq)+heat\]
done
clear
View Answer play_arrow
question_answer 86) The number of chiral centres in \[(+)-\]glucose
A)
4
done
clear
B)
3
done
clear
C)
2
done
clear
D)
1
done
clear
View Answer play_arrow
question_answer 87) Aniline on oxidation with \[\text{N}{{\text{a}}_{\text{2}}}\text{C}{{\text{r}}_{\text{2}}}{{\text{O}}_{\text{7}}}\]and \[{{\text{H}}_{\text{2}}}\text{S}{{\text{O}}_{\text{4}}}\]gives
A)
benzoic acid
done
clear
B)
\[m-\] amino benzoic acid
done
clear
C)
Schiff?s base
done
clear
D)
\[~p-\] benzoquinone
done
clear
View Answer play_arrow
question_answer 88) What are the units of equivalent conductivity of a solution?
A)
\[\text{mho c}{{\text{m}}^{-1}}\]
done
clear
B)
\[\text{ohm c}{{\text{m}}^{-1}}\text{ g equi}{{\text{v}}^{-1}}\]
done
clear
C)
\[\text{mho c}{{\text{m}}^{-2}}\text{ g equi}{{\text{v}}^{-1}}\]
done
clear
D)
\[\text{mho c}{{\text{m}}^{2}}\text{ g equi}{{\text{v}}^{-1}}\]
done
clear
View Answer play_arrow
question_answer 89) What is the cell reaction occurring in Daniel cell (Galvanic cell)?
A)
\[Cu(s)+ZnS{{O}_{4}}(aq)\to CuS{{O}_{4}}(aq)+Zn(s)\]
done
clear
B)
\[Zn(s)+CuS{{O}_{4}}(aq)\to Cu(s)+ZnS{{O}_{4}}(aq)\]
done
clear
C)
\[Ni(s)+ZnS{{O}_{4}}(aq)\to NiS{{O}_{4}}(aq)+Zn(s)\]
done
clear
D)
\[2Na(s)+CdS{{O}_{4}}(aq)\to N{{a}_{2}}S{{O}_{4}}(aq)\]\[+\,Cd(s)\]
done
clear
View Answer play_arrow
question_answer 90) \[n-\]propylamine yields a volatile compound X on warming with ale. alkali and chloroform. X has an offensive odour. The structure of X is
A)
\[~C{{H}_{3}}C{{H}_{2}}C{{H}_{2}}CN\]
done
clear
B)
\[~{{(C{{H}_{3}})}_{2}}CHCN\]
done
clear
C)
\[~C{{H}_{3}}C{{H}_{2}}C{{H}_{2}}NC\]
done
clear
D)
\[{{(C{{H}_{3}})}_{2}}CHNC\]
done
clear
View Answer play_arrow
question_answer 91) The molecular formula of benzonitrile is
A)
\[{{C}_{6}}{{H}_{5}}CN\]
done
clear
B)
\[{{C}_{6}}{{H}_{5}}NC\]
done
clear
C)
\[{{C}_{6}}{{H}_{5}}CNO\]
done
clear
D)
\[{{C}_{6}}{{H}_{5}}NCO\]
done
clear
View Answer play_arrow
question_answer 92) Which of the following statements (or equation) is correct?
A)
The units of cell emf are\[\text{V}\text{.c}{{\text{m}}^{-1}}\]
done
clear
B)
\[\Delta G=-\frac{nF}{{{E}_{cell}}}\]
done
clear
C)
In Galvanic cell, chemical energy is transformed into electrical energy
done
clear
D)
Oxidation state of Mn in potassium permanganate is + 6
done
clear
View Answer play_arrow
question_answer 93) Which of the following metal can be obtained by the electrolysis of the aqueous solution of its salts?
A)
Cu
done
clear
B)
Na
done
clear
C)
Mg
done
clear
D)
K
done
clear
View Answer play_arrow
question_answer 94) The magnetic moment (in BM) of \[\text{Z}{{\text{n}}^{\text{2+}}}\]ion according to spin-only formula is
A)
zero
done
clear
B)
1.73
done
clear
C)
2.84
done
clear
D)
3.87
done
clear
View Answer play_arrow
question_answer 95) The 3d-block element that exhibits maximum number of oxidation states is
A)
Sc
done
clear
B)
Ti
done
clear
C)
Mn
done
clear
D)
Zn
done
clear
View Answer play_arrow
question_answer 96) Which of the following molecule in its valence shell has three bond pairs of electrons and one lone pair of electrons?
A)
\[N{{H}_{3}}\]
done
clear
B)
\[~{{H}_{2}}O\]
done
clear
C)
\[~B{{F}_{3}}\]
done
clear
D)
\[~C{{O}_{2}}\]
done
clear
View Answer play_arrow
question_answer 97) Which of the following set of properties belong to\[PC{{l}_{5}}\]?
A)
\[s{{p}^{3}},\] tetrahedral, 4 valence shell pairs of electrons
done
clear
B)
trigonal bipyramidal, 5 valence shell pairs of electrons
done
clear
C)
\[s{{p}^{3}}{{d}^{2}},\]octahedral, 6 valence shell pairs of electrons
done
clear
D)
\[s{{p}^{3}}d,\]square planar, 4 valence shell pairs of electrons
done
clear
View Answer play_arrow
question_answer 98) The metal ion in complex \[\underset{\scriptscriptstyle-}{A}\]has BAN identical to the atomic number of krypton. \[\underset{\scriptscriptstyle-}{A}\]is (At. no. of\[Cr=24,\,Fe=26,\,Pd=46\])
A)
\[[Pd{{(N{{H}_{3}})}_{6}}]C{{l}_{4}}\]
done
clear
B)
\[[Cr{{(N{{H}_{3}})}_{5}}Cl]S{{O}_{4}}\]
done
clear
C)
\[N{{a}_{4}}[Fe{{(CN)}_{6}}]\]
done
clear
D)
\[{{K}_{3}}[Fe{{(CN)}_{6}}]\]
done
clear
View Answer play_arrow
question_answer 99) The complex that does not give a precipitate wit\[\text{ }\!\!~\!\!\text{ AgN}{{\text{O}}_{\text{3}}}\]solution
A)
\[[Co{{(N{{H}_{3}})}_{3}}C{{l}_{3}}]\]
done
clear
B)
\[[Co{{(N{{H}_{3}})}_{6}}]C{{l}_{3}}\]
done
clear
C)
\[\text{ }\!\![\!\!\text{ Ag(N}{{\text{H}}_{\text{3}}}{{\text{)}}_{\text{2}}}\text{ }\!\!]\!\!\text{ Cl}\]
done
clear
D)
\[[Cr{{(N{{H}_{3}})}_{4}}C{{l}_{2}}]Cl\]
done
clear
View Answer play_arrow
question_answer 100) According to bond order concept, the correct order of stability of\[{{\text{O}}_{\text{2}}}\text{,O}_{\text{2}}^{\text{+}}\] and \[\text{O}_{2}^{-}\] is
A)
\[{{O}_{2}}>O_{2}^{+}>O_{2}^{-}\]
done
clear
B)
\[O_{2}^{-}>{{O}_{2}}>O_{2}^{+}\]
done
clear
C)
\[{{O}_{2}}>O_{2}^{-}>O_{2}^{+}\]
done
clear
D)
\[O_{2}^{+}>{{O}_{2}}<O_{2}^{-}\]
done
clear
View Answer play_arrow
question_answer 101) Zero dipole moment is possessed by
A)
\[PC{{l}_{3}}\]
done
clear
B)
\[~B{{F}_{3}}\]
done
clear
C)
\[Cl{{F}_{3}}\]
done
clear
D)
\[~N{{H}_{3}}\]
done
clear
View Answer play_arrow
question_answer 102) The number of moles of ions given on complete ionisation of one mole of \[[Co{{(N{{H}_{3}})}_{6}}]C{{l}_{3}}\] is/are
A)
4
done
clear
B)
3
done
clear
C)
2
done
clear
D)
1
done
clear
View Answer play_arrow
question_answer 103) The coordination number in a/an........ complex may increase to 8.
A)
cobalt
done
clear
B)
osmium
done
clear
C)
nickel
done
clear
D)
iron
done
clear
View Answer play_arrow
question_answer 104) The radius ratio \[\left( \frac{{{r}^{+}}}{{{r}^{-}}} \right)\] of an ionic solid\[({{A}^{+}}{{B}^{-}})\]is 0.69. What is the coordination number of\[{{B}^{-}}\]?
A)
6
done
clear
B)
8
done
clear
C)
2
done
clear
D)
10
done
clear
View Answer play_arrow
question_answer 105) A, B and C are ideal gases. Their molecular weights are 2, 4 and 28 respectively. The ran of diffusion of these gases follow the order
A)
\[C>A>B\]
done
clear
B)
\[~C>B>A\]
done
clear
C)
\[A=B=C\]
done
clear
D)
\[~A>B>C\]
done
clear
View Answer play_arrow
question_answer 106) Among the following ions (hydrated), the colourless metal ion is
A)
\[C{{u}^{+}}\]
done
clear
B)
\[C{{u}^{2+}}\]
done
clear
C)
\[F{{e}^{2+}}\]
done
clear
D)
\[M{{n}^{2+}}\]
done
clear
View Answer play_arrow
question_answer 107) German silver is an alloy of
A)
\[Cu,Zn\]
done
clear
B)
\[~Cu,Ni,\,Zn\]
done
clear
C)
\[~Cu,Sn,Zn\]
done
clear
D)
\[~Cu,Zn\]
done
clear
View Answer play_arrow
question_answer 108) Which of the following Statements is not correct?
A)
The units of surface tension are dynes \[c{{m}^{-1}}\]
done
clear
B)
The units of viscosity coefficient of a liquid are "poise"
done
clear
C)
\[\text{CsCl}\]crystallizes in body centred cubic type of lattice
done
clear
D)
The coordination number of \[{{\text{S}}^{2-}}\]in ZnS is 6
done
clear
View Answer play_arrow
question_answer 109) Which of the following is not a method of preparation of colloidal solution?
A)
Electrical dispersion
done
clear
B)
Peptization
done
clear
C)
Coagulation
done
clear
D)
Mechanical dispersion
done
clear
View Answer play_arrow
question_answer 110) Pauling's equation for determining the electronegativity of an element, is
A)
\[{{X}_{A}}-{{X}_{B}}=0.208\sqrt{\Delta }\]
done
clear
B)
\[{{X}_{A}}+{{X}_{B}}=0.208\sqrt{\Delta }\]
done
clear
C)
\[{{X}_{A}}-{{X}_{B}}=0.208{{\Delta }^{2}}\]
done
clear
D)
\[{{X}_{A}}-{{X}_{B}}=\sqrt{\Delta }\] \[{{X}_{A}},{{X}_{B}}=\]electronegativity values of elements AandB \[\Delta =\]represents polarity of \[A-B\]bond
done
clear
View Answer play_arrow
question_answer 111) The ionic radii\[(\overset{\text{o}}{\mathop{A}}\,)\]of \[{{C}^{4-}}\]and\[{{O}^{2-}}\]respectively are 2.60 and 1.40. The ionic radius of th6 isoelectronic ion \[{{N}^{3-}}\]would be
A)
2.6
done
clear
B)
1.71
done
clear
C)
1.4
done
clear
D)
0.95
done
clear
View Answer play_arrow
question_answer 112) The gold numbers of some colloidal solution are given below Colloidal solution Gold number A 0.01 B 2.5 C 20 The protective nature of these colloidal solutions follow the order
A)
\[~C>B>A\]
done
clear
B)
\[~A>B>C\]
done
clear
C)
\[~A=B=C\]
done
clear
D)
\[~B>A>C\]
done
clear
View Answer play_arrow
question_answer 113) Which of the following reaction is an example for homogeneous catalysis?
A)
\[2{{H}_{2}}{{O}_{2}}(l)\xrightarrow{Mn{{O}_{2}}(s)}2{{H}_{2}}O(l)+{{O}_{2}}(g)\]
done
clear
B)
\[2S{{O}_{2}}(g)+{{O}_{2}}(g)2S{{O}_{3}}(g)\]
done
clear
C)
\[2CO(g)+{{O}_{2}}(g)\xrightarrow{NO(g)}2C{{O}_{2}}(g)\]
done
clear
D)
\[{{H}_{2}}(g)+{{C}_{2}}{{H}_{4}}(g)\xrightarrow{Ni(s)}{{C}_{3}}{{H}_{6}}(g)\]
done
clear
View Answer play_arrow
question_answer 114) Consider the following abbreviations for hydrated alkali ions \[X={{[Li{{({{H}_{2}}O)}_{n}}]}^{+}}\] \[X={{[K{{({{H}_{2}}O)}_{n}}]}^{+}}\] \[Z={{[Cs{{({{H}_{2}}O)}_{n}}]}^{+}}\] What is the correct order of size of these hydrated alkali ions?
A)
\[~X>Y>Z\]
done
clear
B)
\[~Z>Y>X\]
done
clear
C)
\[~X=Y=Z\]
done
clear
D)
\[~Z>X>Y\]
done
clear
View Answer play_arrow
question_answer 115) What is the product formed when phosphorus trioxide is dissolved in water?
A)
\[~HP{{O}_{3}}\]
done
clear
B)
\[~{{H}_{3}}P{{O}_{4}}\]
done
clear
C)
\[~{{H}_{3}}P{{O}_{3}}\]
done
clear
D)
\[~HP{{O}_{2}}\]
done
clear
View Answer play_arrow
question_answer 116) The molecular formula of dithionic acid is
A)
\[~{{H}_{2}}{{S}_{2}}{{O}_{4}}\]
done
clear
B)
\[~{{H}_{2}}{{S}_{2}}{{O}_{6}}\]
done
clear
C)
\[~{{H}_{2}}{{S}_{2}}{{O}_{5}}\]
done
clear
D)
\[{{H}_{2}}{{S}_{2}}{{O}_{7}}\]
done
clear
View Answer play_arrow
question_answer 117) The bond dissociation energy of \[\text{C}{{\text{l}}_{\text{2}}}\text{, B}{{\text{r}}_{\text{2}}}\]and \[{{\text{I}}_{\text{2}}}\]follow the order
A)
\[~C{{l}_{2}}>{{I}_{2}}>B{{r}_{2}}\]
done
clear
B)
\[{{I}_{2}}>B{{r}_{2}}>C{{l}_{2}}\]
done
clear
C)
\[{{I}_{2}}=C{{l}_{2}}=B{{r}_{2}}\]
done
clear
D)
\[C{{l}_{2}}>B{{r}_{2}}>{{I}_{2}}\]
done
clear
View Answer play_arrow
question_answer 118) During the extraction of copper, the impurity \[(FeS)\]is removed as slag by mixing the contaminated copper ore with silica and coke. The molecular formula of slag is
A)
\[~FeSi{{O}_{3}}\]
done
clear
B)
\[~F{{e}_{2}}{{O}_{3}}\]
done
clear
C)
\[FeSi\](solid)
done
clear
D)
\[~FeSi\] (vapour)
done
clear
View Answer play_arrow
question_answer 119) Which of the following is used as indelible ink?
A)
Aqueous \[\text{CuS}{{\text{O}}_{\text{4}}}\]solution
done
clear
B)
Aqueous \[\text{AgN}{{\text{O}}_{\text{3}}}\]solution
done
clear
C)
Aqueous \[\text{NaCl}\]solution
done
clear
D)
Aqueous \[\text{NaOH}\]solution
done
clear
View Answer play_arrow
question_answer 120) Which of the following ore is an ore of copper?
A)
Argentite
done
clear
B)
Haematite
done
clear
C)
Malachite
done
clear
D)
Calamine
done
clear
View Answer play_arrow
question_answer 121) \[\text{KMn}{{\text{O}}_{\text{4}}}(mol\,wt.=158)\]oxidizes oxalic acid in acid medium to \[\text{C}{{\text{O}}_{\text{2}}}\]and water as follows \[5{{C}_{2}}O_{4}^{2-}+2MnO_{4}^{-}+16{{H}^{+}}\to 10C{{O}_{2}}+2M{{n}^{2+}}\]\[\text{+}\,\,\text{8}{{\text{H}}_{\text{2}}}\text{O}\] What is the equivalent weight of\[\text{KMn}{{\text{O}}_{\text{4}}}\]?
A)
158
done
clear
B)
31.6
done
clear
C)
39.5
done
clear
D)
79
done
clear
View Answer play_arrow
question_answer 122) Sodium bicarbonate on heating decomposes to form sodium carbonate, \[\text{C}{{\text{O}}_{\text{2}}}\]and water. If 0.2 moles of sodium bicarbonate is completely decomposed, how many moles of sodium carbonate is formed?
A)
0.1
done
clear
B)
0.2
done
clear
C)
0.05
done
clear
D)
0.025
done
clear
View Answer play_arrow
question_answer 123) What is the energy (in eV) required to excite the electron from\[n=1\]to\[n=2\]state in hydrogen atom? (\[n=\]principal quantum number)
A)
13.6
done
clear
B)
3.4
done
clear
C)
17.0
done
clear
D)
10.2
done
clear
View Answer play_arrow
question_answer 124) According to aufbau principle, the correct order of energy of 3d, 4s and 4p orbitals is
A)
\[~4p<3d<4s\]
done
clear
B)
\[~4s<4p<3d\]
done
clear
C)
\[~4s<3d<4p\]
done
clear
D)
\[~3d<4s<4p\]
done
clear
View Answer play_arrow
question_answer 125) \[n-\]pentane and 2-methylbutane are a pair of
A)
enantiomers
done
clear
B)
stereoisomers
done
clear
C)
diastereomers
done
clear
D)
constitutional isomers
done
clear
View Answer play_arrow
question_answer 126)
A)
geometrical isomerism
done
clear
B)
tautomerism
done
clear
C)
optical isomerism
done
clear
D)
geometrical and optical isomerism
done
clear
View Answer play_arrow
question_answer 127) The activity of a radioactive nuclide is \[2\times {{10}^{7}}\] disintegrations per minute (dpm). After 23.03 min, its activity is reduced to\[2\times {{10}^{6}}\text{ dpm}\text{.}\] What is the average life (in min) of this nuclide?
A)
100
done
clear
B)
10
done
clear
C)
1
done
clear
D)
0.1
done
clear
View Answer play_arrow
question_answer 128) What' is the correct order of velocity of alpha \[(\alpha ),\]beta \[(\beta )\]and gamma\[(\gamma )\]rays?
A)
\[\alpha >\,\beta >\gamma \]
done
clear
B)
\[\alpha >\,\gamma >\beta \]
done
clear
C)
\[\gamma >\,\alpha >\beta \]
done
clear
D)
\[\gamma >\beta >\alpha \]
done
clear
View Answer play_arrow
question_answer 129) The isomers which are interconverted through rotation around a single bond are
A)
conformers
done
clear
B)
diastereomers
done
clear
C)
enantiomers
done
clear
D)
position isomers
done
clear
View Answer play_arrow
question_answer 130) The major product in the reaction of 2-butyne with \[\text{Li/liq}\text{.N}{{\text{H}}_{\text{3}}}\]is
A)
done
clear
B)
done
clear
C)
\[C{{H}_{3}}C{{H}_{2}}C{{H}_{2}}C{{H}_{3}}\]
done
clear
D)
\[{{H}_{2}}C=CH-C{{H}_{2}}-C{{H}_{3}}\]
done
clear
View Answer play_arrow
question_answer 131) What is X in the following nuclear reaction? \[_{11}N{{a}^{23}}+{{\,}_{0}}{{n}^{1}}\to {{\,}_{11}}N{{a}^{24}}+X\]
A)
\[{{\,}_{1}}{{H}^{1}}\]
done
clear
B)
\[{{\,}_{2}}H{{e}^{4}}\]
done
clear
C)
\[{{\,}_{1}}{{H}^{2}}\]
done
clear
D)
\[\gamma -\]ray (gamma ray)
done
clear
View Answer play_arrow
question_answer 132) HA is a weak acid. The pH of 0.1 M HA solution is 2. What is the degree of dissociation \[(\alpha )\]of HA?
A)
0.5
done
clear
B)
0.2
done
clear
C)
0.1
done
clear
D)
0.301
done
clear
View Answer play_arrow
question_answer 133) In the following reaction, A and B, respectively are \[A\xrightarrow{\text{HBr}}{{C}_{2}}{{H}_{5}}Br\xrightarrow{B}A\]
A)
\[{{C}_{2}}{{H}_{4}},alc\,KOH/\Delta \]
done
clear
B)
\[{{C}_{2}}{{H}_{5}}Cl,aq\,KOH/\Delta \]
done
clear
C)
\[C{{H}_{3}}OH,aq\,KOH/\Delta \]
done
clear
D)
\[{{C}_{2}}{{H}_{2}},PB{{r}_{3}}\]
done
clear
View Answer play_arrow
question_answer 134) The reagent(s) used in the preparation of aspirin from salicylic acid
A)
\[\text{SOC}{{\text{l}}_{\text{2}}}\text{,}\]pyridine
done
clear
B)
\[{{\text{(C}{{\text{H}}_{3}}\text{CO)}}_{2}}O,{{H}^{+}}\]
done
clear
C)
\[C{{H}_{3}}C{{O}_{2}}H,HCl\]
done
clear
D)
\[C{{H}_{3}}Cl,AlC{{l}_{3}}\]
done
clear
View Answer play_arrow
question_answer 135) The equilibrium reaction that is not influenced by volume change at constant temperature is
A)
\[{{H}_{2}}(g)+{{I}_{2}}(g)2HI(g)\]
done
clear
B)
\[{{N}_{2}}(g)+3{{H}_{2}}(g)2N{{H}_{3}}(g)\]
done
clear
C)
\[{{N}_{2}}{{O}_{4}}(g)2N{{O}_{2}}(g)\]
done
clear
D)
\[2NO(g)+{{O}_{2}}2N{{O}_{2}}(g)\]
done
clear
View Answer play_arrow
question_answer 136) Consider the following solutions of equal concentrations \[A=N{{H}_{4}}Cl\] \[B=C{{H}_{3}}COONa\] \[C=N{{H}_{2}}OH\] \[D=C{{H}_{2}}COOH\] A buffer solution can be obtained by mixing equal volumes of
A)
C and D
done
clear
B)
A and B
done
clear
C)
A and C
done
clear
D)
C and D
done
clear
View Answer play_arrow
question_answer 137) In the following reaction, X and Y respectively are \[{{C}_{2}}{{H}_{5}}OH\xrightarrow{KMn{{O}_{4}}/{{H}^{+}}}X\frac{Y}{{{H}_{2}}S{{O}_{4}}/\Delta }C{{H}_{3}}C{{O}_{2}}{{C}_{2}}{{H}_{5}}\]
A)
\[C{{H}_{3}}OH,{{C}_{2}}{{H}_{5}}OH\]
done
clear
B)
\[~C{{H}_{3}}CHO,C{{H}_{3}}OH\]
done
clear
C)
\[~C{{H}_{3}}C{{O}_{2}}H,\text{ }{{C}_{2}}{{H}_{5}}OH\]
done
clear
D)
\[~{{C}_{2}}{{H}_{4}},C{{H}_{3}}CO{{}_{2}}H\]
done
clear
View Answer play_arrow
question_answer 138) The reaction conditions used for converting 1, 2-dibromopropane to propylene are
A)
\[KOH,alcohol/\Delta \]
done
clear
B)
\[KOH,\text{ }water/\Delta \]
done
clear
C)
\[~Zn,\text{ }alcohol/\Delta \]
done
clear
D)
\[~Na,\text{ }alcohol/\Delta \]
done
clear
View Answer play_arrow
question_answer 139) Which of the following's a Lewis acid?
A)
\[AlC{{l}_{3}}\]
done
clear
B)
\[C{{l}^{-}}\]
done
clear
C)
\[CO\]
done
clear
D)
\[{{C}_{2}}{{H}_{2}}\]
done
clear
View Answer play_arrow
question_answer 140) If "a" and\[''{{t}_{1/2}}''\] are initial concentration of reactant and half-life of a zero order reaction respectively, which of the following is correct?
A)
\[{{t}_{1/2}}\propto \frac{1}{a}\]
done
clear
B)
\[{{t}_{1/2}}\propto a\]
done
clear
C)
\[{{t}_{1/2}}\propto \frac{1}{{{a}^{2}}}\]
done
clear
D)
\[{{t}_{1/2}}\propto {{a}^{2}}\]
done
clear
View Answer play_arrow
question_answer 141) All monosaccharides ....... Tollen's reagent.
A)
oxidises
done
clear
B)
condense with
done
clear
C)
reduces
done
clear
D)
add to
done
clear
View Answer play_arrow
question_answer 142) The product formed in the reaction of glycine with benzoyl chloride \[\text{+ aq NaOH}\]is
A)
\[~PhCOC{{H}_{2}}N{{H}_{2}}\]
done
clear
B)
\[~PhC{{H}_{2}}N{{H}_{2}}\]
done
clear
C)
\[~PhCONHC{{H}_{3}}\]
done
clear
D)
\[~PhCONHC{{H}_{2}}C{{O}_{2}}H\]
done
clear
View Answer play_arrow
question_answer 143) The rate constant of a reaction is found to be \[3\times {{10}^{-3}}\,mol\,{{L}^{-1}}\,{{\min }^{-1}}.\]The order of the reaction is
A)
zero
done
clear
B)
1
done
clear
C)
2
done
clear
D)
1.5
done
clear
View Answer play_arrow
question_answer 144) What is the two third life of a first order reaction having \[k=5.48\times {{10}^{-14}}{{s}^{-1}}\]
A)
\[2.01\times {{10}^{11}}s\]
done
clear
B)
\[2.01\times {{10}^{13}}s\]
done
clear
C)
\[8.08\times {{10}^{13}}\,s\]
done
clear
D)
\[16.04\times {{10}^{11}}\,s\]
done
clear
View Answer play_arrow
question_answer 145) Which of the following solvents are aprotic? [A]\[N{{H}_{3}}\] [B]\[S{{O}_{2}}\] [C] \[C{{H}_{3}}CN\] [D] \[C{{H}_{3}}C{{O}_{2}}H\]
A)
\[A,B,C\]
done
clear
B)
\[A,C,D\]
done
clear
C)
\[B,C\]
done
clear
D)
\[A,C\]
done
clear
View Answer play_arrow
question_answer 146) Chlorobenzene is o, p -directing in electrophilic substitution reaction. The directing influence is explained by
A)
\[+\text{ }M\]of\[Ph\]
done
clear
B)
\[+\,I\]of \[Cl\]
done
clear
C)
\[+\text{ }M\]of\[Cl\]
done
clear
D)
\[-I\]of \[Ph\]
done
clear
View Answer play_arrow
question_answer 147) 5 L of a solution contains\[\text{25}\,\text{mg}\] of \[\text{CaC}{{\text{O}}_{3}}.\]What is its concentration in ppm? (mol. wt. of \[\text{CaC}{{\text{O}}_{\text{3}}}\]is 100)
A)
25
done
clear
B)
1
done
clear
C)
5
done
clear
D)
2500
done
clear
View Answer play_arrow
question_answer 148) Observe the following abbrevations \[{{\pi }_{obs}}=\]observed colligative property \[{{\pi }_{cal}}=\]theoretical colligative property assuming normal behaviour of solute. van't Hoff factor \[(i)\]is given by
A)
\[i={{\pi }_{obs}}\times {{\pi }_{cal}}\]
done
clear
B)
\[i={{\pi }_{obs}}+{{\pi }_{cal}}\]
done
clear
C)
\[i={{\pi }_{obs}}-{{\pi }_{cal}}\]
done
clear
D)
\[i=\frac{{{\pi }_{obs}}}{{{\pi }_{cal}}}\]
done
clear
View Answer play_arrow
question_answer 149) The correct order for homolytic bond dissociation energies (\[\Delta H\]in kcal/mol) for \[C{{H}_{4}}(A),{{C}_{2}}{{H}_{6}}(B)\]and\[C{{H}_{3}}Br(C),\]under identical experimental conditions
A)
\[C>B>A\]
done
clear
B)
\[B>C>A\]
done
clear
C)
\[~C>A>B\]
done
clear
D)
\[~A>B>C\]
done
clear
View Answer play_arrow
question_answer 150) \[RX+{{I}^{-}}\xrightarrow{{}}R-I+X\]is an example of....... reaction.
A)
nucleophilic addition
done
clear
B)
nucleophilic substitution
done
clear
C)
electrophilic addition
done
clear
D)
elimination
done
clear
View Answer play_arrow
question_answer 151) If \[a{{x}^{3}}+b{{x}^{2}}+ex+d=0\]has a repeated root \[\alpha ,\] then a is also a root of
A)
\[3a{{x}^{2}}+2bx+d=0\]
done
clear
B)
\[a{{x}^{2}}+b\,x+c=0\]
done
clear
C)
\[3a{{x}^{2}}+2bx+c=0\]
done
clear
D)
\[6ax+2b=0\]
done
clear
View Answer play_arrow
question_answer 152) If the roots of \[{{x}^{3}}-3{{x}^{2}}-6x+8=0\] are in arithmetic progression, then the roots of the equation are
A)
\[3,4,5\]
done
clear
B)
\[4,7,10\]
done
clear
C)
\[-2,1,4\]
done
clear
D)
\[1,4,7\]
done
clear
View Answer play_arrow
question_answer 153) If \[\alpha ,\beta ,\gamma \] are the roots of the cubic equation \[{{x}^{3}}-{{x}^{2}}+x-1=0,\]then \[{{\alpha }^{-3}}+{{\beta }^{-3}}+{{\gamma }^{-3}}\] is equal to
A)
\[1\]
done
clear
B)
\[2\]
done
clear
C)
\[3\]
done
clear
D)
\[4\]
done
clear
View Answer play_arrow
question_answer 154) If \[\alpha ,\beta ,\gamma \] are the roots of \[{{x}^{3}}+bx+c=0,\]then \[{{\alpha }^{2}}\beta +\alpha {{\beta }^{2}}+{{\beta }^{2}}\gamma +{{\gamma }^{2}}\alpha +\gamma {{\alpha }^{2}}\] is equal to
A)
\[c\]
done
clear
B)
\[-c\]
done
clear
C)
\[-3c\]
done
clear
D)
\[3c\]
done
clear
View Answer play_arrow
question_answer 155) \[\underset{x\to \infty }{\mathop{\lim }}\,(\sqrt{x+\sqrt{x}}-\sqrt{x})\]
A)
\[-1/2\]
done
clear
B)
\[1/2\]
done
clear
C)
\[1\]
done
clear
D)
\[0\]
done
clear
View Answer play_arrow
question_answer 156) \[\underset{x\to 1}{\mathop{\lim }}\,\frac{2{{x}^{2}}+x-3}{3{{x}^{2}}+2x-2}\]is equal to
A)
\[1\]
done
clear
B)
\[2\]
done
clear
C)
\[-1\]
done
clear
D)
\[-2\]
done
clear
View Answer play_arrow
question_answer 157) \[\underset{x\to 0}{\mathop{\lim }}\,\frac{{{\sin }^{-1}}x-x}{{{x}^{3}}\,\cos x}\]is equal to
A)
\[1/2\]
done
clear
B)
\[1/3\]
done
clear
C)
\[1/6\]
done
clear
D)
\[1/12\]
done
clear
View Answer play_arrow
question_answer 158) If \[f:R\to R\] given by \[f(x)=\left\{ \begin{matrix} 2\,\cos x, & if & x\le -\frac{\pi }{2} \\ a\,\sin \,x+b, & if & -\frac{\pi }{2}<x<\frac{\pi }{2} \\ 1+{{\cos }^{2}}x, & if & x\ge \frac{\pi }{2} \\ \end{matrix} \right.\] is a continuous function on R, then (a, b) is equal to
A)
\[(1/2,\,1/2)\]
done
clear
B)
\[(0,-1)\]
done
clear
C)
\[(0,2)\]
done
clear
D)
\[(1,0)\]
done
clear
View Answer play_arrow
question_answer 159) \[\frac{d}{dx}\left\{ \begin{align} & {{\tan }^{-1}}\left( \frac{2x}{1-{{x}^{2}}} \right)+{{\tan }^{-1}}\left( \frac{3x-{{x}^{2}}}{1-3{{x}^{2}}} \right) \\ & -{{\tan }^{-1}}\left( \frac{4x-4{{x}^{2}}}{1-6{{x}^{2}}+{{x}^{4}}} \right) \\ \end{align} \right\}\]equal to
A)
\[\frac{1}{\sqrt{1-{{x}^{2}}}}\]
done
clear
B)
\[-\frac{1}{\sqrt{1-{{x}^{2}}}}\]
done
clear
C)
\[\frac{1}{1+{{x}^{2}}}\]
done
clear
D)
\[-\frac{1}{1+{{x}^{2}}}\]
done
clear
View Answer play_arrow
question_answer 160) If \[2{{x}^{2}}-3xy+{{y}^{2}}+x-2y-8=0,\]then \[\frac{dy}{dx}\] is equal to
A)
\[\frac{3y-4x-1}{2y-3x-2}\]
done
clear
B)
\[\frac{3y+4x-1}{2y+3x+2}\]
done
clear
C)
\[\frac{3y+4x+1}{2y-3x+2}\]
done
clear
D)
\[\frac{3y+4x+1}{2y-3x-2}\]
done
clear
View Answer play_arrow
question_answer 161) The equation of the tangent at \[(1,5)\] to the curve \[y=5{{x}^{4}}\] is
A)
\[20x-y=15\]
done
clear
B)
\[x+20y=101\]
done
clear
C)
\[20x+y=15\]
done
clear
D)
\[x-20y=101\]
done
clear
View Answer play_arrow
question_answer 162) The length of the sub tangent at any point \[({{x}_{1}},\,{{y}_{1}})\] on the curve \[y={{a}^{x}},\]\[(a>0)\] is
A)
\[2\,\,\log \,a\]
done
clear
B)
\[1/\,\,\log \,a\]
done
clear
C)
\[\log \,a\]
done
clear
D)
\[{{a}^{{{2}_{{{x}_{1}}}}}}\log \,a\]
done
clear
View Answer play_arrow
question_answer 163) The set \[\{{{x}^{3}}-12x:-3\le x\le 3\}\] is equal to
A)
\[\{x:-16\le x\le 16\}\]
done
clear
B)
\[\{x:-12\le x\le 12\}\]
done
clear
C)
\[\{x:-9\le x\le 9\}\]
done
clear
D)
\[\{x:0\le x\le 10\}\]
done
clear
View Answer play_arrow
question_answer 164) The set of all local maxima for \[y=\cos \,\,x\]is
A)
\[\{n\pi :n\in I\}\]
done
clear
B)
\[\{2n\pi :n\in I\}\]
done
clear
C)
\[\{n\pi /2:n\in I\}\]
done
clear
D)
\[\{n\pi /3:n\in I\}\]
done
clear
View Answer play_arrow
question_answer 165) The absolute maximum of \[{{x}^{40}}-{{x}^{20}}\]on the interval \[[0,1]\] is
A)
\[-1/4\]
done
clear
B)
\[0\]
done
clear
C)
\[1/4\]
done
clear
D)
\[1/2\]
done
clear
View Answer play_arrow
question_answer 166) \[\int_{-2}^{2}{(x-|x|)}\,\,dx\] is equal to
A)
\[0\]
done
clear
B)
\[2\]
done
clear
C)
\[4\]
done
clear
D)
\[-4\]
done
clear
View Answer play_arrow
question_answer 167) If \[\int{\frac{dx}{x\,\log \,x}}=f(x)+\] constant, then \[f(x)\] is equal to
A)
\[1/\,\log \,x\]
done
clear
B)
\[\log \,x\]
done
clear
C)
\[\log \,\,\log \,x\]
done
clear
D)
\[x/\,\log \,x\]
done
clear
View Answer play_arrow
question_answer 168) If \[\int{\text{cosec x}\,\text{dx =f(x)+}}\] constant, then \[f(x)\] is equal to
A)
\[\tan \,x/2\]
done
clear
B)
\[\log \,|\tan \,(x/2)|\]
done
clear
C)
\[\log |\sin \,x|\]
done
clear
D)
\[\log |cos\,x|\]
done
clear
View Answer play_arrow
question_answer 169) \[{{I}_{n}}=\int{{{\tan }^{n}}x}\,\,dx\] for \[n\ge 2,\] then \[{{I}_{n}}+{{I}_{n-2}}\] is equal to
A)
\[{{\tan }^{n\,}}x+c\]
done
clear
B)
\[\frac{({{\tan }^{n-1}}x)}{n-1}+c\]
done
clear
C)
\[\frac{{{\tan }^{n}}x}{n}+c\]
done
clear
D)
\[n\,\,{{\tan }^{n}}x+c\]
done
clear
View Answer play_arrow
question_answer 170) \[\int_{0}^{\pi /2}{x\,\sin \,x}\,\,dx\]is equal to
A)
\[0\]
done
clear
B)
\[1\]
done
clear
C)
\[-1\]
done
clear
D)
\[2\]
done
clear
View Answer play_arrow
question_answer 171) The area (in square unit) of the region bounded by the y-axis and the curve \[2x={{y}^{2}}-1\]is
A)
\[1/3\]
done
clear
B)
\[2/3\]
done
clear
C)
\[1\]
done
clear
D)
\[2\]
done
clear
View Answer play_arrow
question_answer 172) The solution of the differential equation \[({{x}^{2}}+{{y}^{2}})dx=2xy\,\,dy\]is
A)
\[{{x}^{2}}+{{y}^{2}}=cy\]
done
clear
B)
\[c({{x}^{2}}-{{y}^{2}})=x\]
done
clear
C)
\[{{x}^{2}}-{{y}^{2}}=cy\]
done
clear
D)
\[{{x}^{2}}+{{y}^{2}}=cx\] (here c is an arbitrary constant)
done
clear
View Answer play_arrow
question_answer 173) A number n is chosen at random from the set \[\{11,12,13,.....30\}.\]The probability that n is neither divisible by 3 nor divisible by 5 is
A)
\[7/20\]
done
clear
B)
\[9/20\]
done
clear
C)
\[11/20\]
done
clear
D)
\[13/20\]
done
clear
View Answer play_arrow
question_answer 174) The probability that a number n chosen at random from 1 to 30, to satisfy \[n+(50/n)>27\]is
A)
\[7/30\]
done
clear
B)
\[3/10\]
done
clear
C)
\[3/5\]
done
clear
D)
\[1/5\]
done
clear
View Answer play_arrow
question_answer 175)
If a random variable X has the distribution given below, then the value of c is \[x=k\] \[-2\] \[-1\] \[0\] \[1\] \[2\] \[3\] \[P(X=k)\] \[\frac{1}{10}\] \[\frac{1}{10}\] \[2c\] \[\frac{3}{10}\] \[\frac{1}{5}\] \[c\]
A)
\[1/5\]
done
clear
B)
\[2/5\]
done
clear
C)
\[1/10\]
done
clear
D)
\[3/10\]
done
clear
View Answer play_arrow
question_answer 176) A random variable X can attain only the value 1, 2, 3, 4, 5 with respective probabilities k, 2k, 3k, 2k, k. If m is the mean of the probability distribution, then (k, m) is equal to
A)
\[(3,\,1/9)\]
done
clear
B)
\[(\,1/9,3)\]
done
clear
C)
\[(\,1/8,4)\]
done
clear
D)
\[(\,1,3)\]
done
clear
View Answer play_arrow
question_answer 177) If \[f(x)=\lambda {{e}^{-ax}}\,\,(a>0)\] for \[0\le x<\infty \] is a probability density, then 'k is equal to
A)
\[a\]
done
clear
B)
\[{{a}^{2}}\]
done
clear
C)
\[1/a\]
done
clear
D)
\[{{a}^{2}}\]
done
clear
View Answer play_arrow
question_answer 178) Two unbiased dice are thrown simultaneously- The probability to get a sum more than 8 is
A)
\[5/36\]
done
clear
B)
\[5/18\]
done
clear
C)
\[5/12\]
done
clear
D)
\[2/9\]
done
clear
View Answer play_arrow
question_answer 179) The moment generating function of a random variable X is
A)
\[E({{e}^{-1X}})\]
done
clear
B)
\[E({{e}^{itX}})\]
done
clear
C)
\[E({{e}^{tX}})\]
done
clear
D)
\[E({{e}^{-it\,X}})\]
done
clear
View Answer play_arrow
question_answer 180) It \[\sigma \] is the standard deviation of a random variable X, then the standard deviation of the random variable \[aX+b,\]where \[a,\text{ }b\in R\]is
A)
\[a\sigma +b\]
done
clear
B)
\[|a|\sigma \]
done
clear
C)
\[|a|\sigma +b\]
done
clear
D)
\[{{a}^{2}}\sigma \]
done
clear
View Answer play_arrow
question_answer 181) If A and B are two sets, then \[A-(A-B)\]is equal to
A)
\[B\]
done
clear
B)
\[A\cup B\]
done
clear
C)
\[A\cap B\]
done
clear
D)
\[B-A\]
done
clear
View Answer play_arrow
question_answer 182) For any real number y the greatest integers not exceeding y is denoted by [y]. If \[f:R\to R\] is defined by \[f(x)=[2x]-2[x]\] for \[x\in R,\] then the range of f is
A)
\[\{x\in R:x>0\}\]
done
clear
B)
\[\{x\in R:x\le 0\}\]
done
clear
C)
\[\{x\in R:0\le x\le 1\}\]
done
clear
D)
\[\{0,\,1\}\]
done
clear
View Answer play_arrow
question_answer 183) The argument of \[\frac{1+i\sqrt{3}}{1-i\sqrt{3}}\] is
A)
\[2\pi /3\]
done
clear
B)
\[\pi /3\]
done
clear
C)
\[-\pi /3\]
done
clear
D)
\[-2\pi /3\]
done
clear
View Answer play_arrow
question_answer 184) If \[S=\left\{ z\in C:\arg \left( \frac{z-2}{z+2} \right)=\frac{\pi }{3} \right\},\] then S is
A)
an ellipse
done
clear
B)
a straight line.
done
clear
C)
a circle
done
clear
D)
a parabola
done
clear
View Answer play_arrow
question_answer 185) If \[ac\ne 0\] and \[\alpha ,\beta \] are the roots of the equation \[a{{x}^{2}}+bx+c=0,\]then the quadratic equation with \[1/\alpha \] and \[1/\beta \] as its root is
A)
\[{{x}^{2}}/a+x/b+1/c=0\]
done
clear
B)
\[c{{x}^{2}}+bx+a=0\]
done
clear
C)
\[b{{x}^{2}}+cx+a=0\]
done
clear
D)
\[a{{x}^{2}}+cx+b=0\]
done
clear
View Answer play_arrow
question_answer 186) If \[\left\{ {{a}_{n}} \right\}_{n}^{x}\] is a sequence with \[{{a}_{0}}=p\] and \[{{a}_{n}}-{{a}_{n-1}}=r{{a}_{n-1}}\] for \[n\ge 1,\] then the terms of the sequence are in
A)
an arithmetic progression
done
clear
B)
a geometric progression
done
clear
C)
a harmonic progression
done
clear
D)
an arithmetico-geometric progression
done
clear
View Answer play_arrow
question_answer 187) The coefficient of \[{{x}^{-17}}\]in the expansion of \[{{\left( {{x}^{4}}-\frac{1}{{{x}^{3}}} \right)}^{15}}\]is
A)
\[^{15}{{C}_{11}}\]
done
clear
B)
\[^{15}{{C}_{12}}\]
done
clear
C)
\[^{-15}{{C}_{11}}\]
done
clear
D)
\[^{-15}{{C}_{3}}\]
done
clear
View Answer play_arrow
question_answer 188) The term independent of x in the expansion of \[{{\left( {{x}^{3}}+\frac{2}{{{x}^{2}}} \right)}^{15}}\] is
A)
\[{{T}_{7}}\]
done
clear
B)
\[{{T}_{8}}\]
done
clear
C)
\[{{T}_{9}}\]
done
clear
D)
\[{{T}_{10}}\]
done
clear
View Answer play_arrow
question_answer 189) The ortho centre of the \[\Delta \,OAB,\]where O is the origin,\[A(6,0)\] and \[B(3,\,3\sqrt{3})\] is
A)
\[(9/2,\,\sqrt{3}/2)\]
done
clear
B)
\[(3,\,\sqrt{3})\]
done
clear
C)
\[(\,\sqrt{3},3)\]
done
clear
D)
\[(3,-\sqrt{3})\]
done
clear
View Answer play_arrow
question_answer 190) The distance between the pair of parallel lines given by \[{{x}^{2}}-1005x+2006=0\]is
A)
\[1001\]
done
clear
B)
\[1000\]
done
clear
C)
\[1005\]
done
clear
D)
\[2006\]
done
clear
View Answer play_arrow
question_answer 191) The radical axis of the coaxial system of circles with limiting points \[(1,2)\] and \[(-2,1)\] is
A)
\[x+3y=0\]
done
clear
B)
\[3x+y=0\]
done
clear
C)
\[2x+3y=0\]
done
clear
D)
\[3x+2y=0\]
done
clear
View Answer play_arrow
question_answer 192) The equation of the circle that can be inscribed in the square OABC, where O is the origin \[A(-2,0),\,B(-2,2)\] and \[C(0,2)\] is
A)
\[{{x}^{2}}+{{y}^{2}}+2x-2y=0\]
done
clear
B)
\[{{x}^{2}}+{{y}^{2}}+2x-2y+1=0\]
done
clear
C)
\[{{x}^{2}}+{{y}^{2}}+2x-2y-1=0\]
done
clear
D)
\[{{x}^{2}}+{{y}^{2}}-2x+2y+1=0\]
done
clear
View Answer play_arrow
question_answer 193) The curve with parametric equation \[x={{e}^{t}}+{{e}^{-t}}\] and \[y={{e}^{t}}-{{e}^{-t}}\] is
A)
a circle
done
clear
B)
an ellipse
done
clear
C)
a hyperbola
done
clear
D)
a parabola
done
clear
View Answer play_arrow
question_answer 194) If \[(-1,\,2\sqrt{2})\] is one of extremity of a focal chord of the parabola \[{{y}^{2}}=-8x,\] then the other extremity is
A)
\[(-1,-\sqrt{2})\]
done
clear
B)
\[(2\sqrt{2},-1)\]
done
clear
C)
\[(-4,4\sqrt{2})\]
done
clear
D)
\[(4,4\sqrt{2})\]
done
clear
View Answer play_arrow
question_answer 195) The equation of the pair of straight lines perpendicular to the pair \[2{{x}^{2}}+3xy+2{{y}^{2}}+10x+5y=0\] and passing through the origin is
A)
\[2{{x}^{2}}+5xy+2{{y}^{2}}=0\]
done
clear
B)
\[2{{x}^{2}}-3xy+2{{y}^{2}}=0\]
done
clear
C)
\[2{{x}^{2}}+3xy+{{y}^{2}}=0\]
done
clear
D)
\[2{{x}^{2}}-5xy+2{{y}^{2}}=0\]
done
clear
View Answer play_arrow
question_answer 196) If two angles of a triangle are \[{{45}^{o}}\] and \[{{\tan }^{-1}}(2),\] then the third angle is
A)
\[{{60}^{o}}\]
done
clear
B)
\[{{75}^{o}}\]
done
clear
C)
\[{{\tan }^{-1}}3\]
done
clear
D)
\[{{90}^{o}}\]
done
clear
View Answer play_arrow
question_answer 197) \[\frac{\tan A}{1+\sec A}+\frac{1+\sec A}{\tan A}\]is equal to
A)
\[2\text{ }sin\text{ }A\]
done
clear
B)
\[2\text{ }cos\text{ }A\]
done
clear
C)
\[2\text{ }cosec\text{ }A\]
done
clear
D)
\[2\text{ }sec\text{ }A\]
done
clear
View Answer play_arrow
question_answer 198) If \[\sin \theta +\cos \theta =h,\] then the quadratic equation having \[\sin \theta \] and \[\cos \theta \] as its roots is
A)
\[{{x}^{2}}-hx+({{h}^{2}}-1)=0\]
done
clear
B)
\[2{{x}^{2}}-2hx+({{h}^{2}}-1)=0\]
done
clear
C)
\[{{x}^{2}}-hx+2({{h}^{2}}-1)=0\]
done
clear
D)
\[{{x}^{2}}-2hx+({{h}^{2}}-1)=0\]
done
clear
View Answer play_arrow
question_answer 199) In a triangle, if \[{{r}_{1}}+{{r}_{3}}=k\,\,{{\cos }^{2}}\,B/2,\]then k is equal to
A)
\[R\]
done
clear
B)
\[2R\]
done
clear
C)
\[3R\]
done
clear
D)
\[4R\]
done
clear
View Answer play_arrow
question_answer 200) If \[\tan (k+1)\theta =\tan \theta ,\] then \[\theta \] belongs to the set
A)
\[\{n\pi :n\in I\}\]
done
clear
B)
\[\{n\pi /2:n\in I\}\]
done
clear
C)
\[\{n\pi /k:n\in I\}\]
done
clear
D)
\[\{n\pi /2k:n\in I\}\]
done
clear
View Answer play_arrow
question_answer 201) \[{{\tan }^{-1}}\left( \frac{3x-{{x}^{3}}}{1-3{{x}^{2}}} \right)-{{\tan }^{-1}}\left( \frac{2x}{1-{{x}^{2}}} \right)\] is equal to
A)
\[0\]
done
clear
B)
\[1\]
done
clear
C)
\[{{\tan }^{-1}}(x)\]
done
clear
D)
\[{{\tan }^{-1}}(2x)\]
done
clear
View Answer play_arrow
question_answer 202) If \[sin\text{ }A:sin\text{ }B:sin\text{ }C=3:4:5,\] then \[cos\text{ }A:cos\text{ }B\]is equal to
A)
\[4:3\]
done
clear
B)
\[5:3\]
done
clear
C)
\[3:4\]
done
clear
D)
\[3:5\]
done
clear
View Answer play_arrow
question_answer 203) If A is a matrix such that \[{{A}^{2}}=A+I,\]where I is the unit matrix, then \[{{A}^{5}}\]is equal to
A)
\[5A+I\]
done
clear
B)
5A + 21
done
clear
C)
\[5A+3I\]
done
clear
D)
\[5A+4I\]
done
clear
View Answer play_arrow
question_answer 204) The inverse of \[\left[ \begin{matrix} 0 & 0 & 2 \\ 0 & 2 & 0 \\ 2 & 0 & 0 \\ \end{matrix} \right]\] is
A)
\[\left[ \begin{matrix} 2 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 2 \\ \end{matrix} \right]\]
done
clear
B)
\[\left[ \begin{matrix} \frac{1}{2} & 0 & 0 \\ 0 & \frac{1}{2} & 0 \\ 0 & 0 & \frac{1}{2} \\ \end{matrix} \right]\]
done
clear
C)
\[\left[ \begin{matrix} 0 & 0 & 2 \\ 0 & 2 & 0 \\ 2 & 0 & 0 \\ \end{matrix} \right]\]
done
clear
D)
\[\left[ \begin{matrix} 0 & 0 & \frac{1}{2} \\ 0 & \frac{1}{2} & 0 \\ \frac{1}{2} & 0 & 0 \\ \end{matrix} \right]\]
done
clear
View Answer play_arrow
question_answer 205) \[\left| \begin{matrix} 1 & 2 & 3 \\ {{1}^{3}} & {{2}^{3}} & {{3}^{3}} \\ {{1}^{5}} & {{2}^{5}} & {{3}^{5}} \\ \end{matrix} \right|\] equal to
A)
\[1!\,\,2\,\,1\,\,\,3\]
done
clear
B)
\[1\,\,!\,\,\,3\,\,!\,\,\,5\,\,!\]
done
clear
C)
\[6\,\,!\]
done
clear
D)
\[9\,\,!\]
done
clear
View Answer play_arrow
question_answer 206) \[\left| \begin{matrix} a & b & a+b \\ b & a+b & a \\ a+b & a & b \\ \end{matrix} \right|\] is equal to
A)
\[{{a}^{3}}+{{b}^{3}}\]
done
clear
B)
\[-({{a}^{3}}+{{b}^{3}})\]
done
clear
C)
\[2\,({{a}^{3}}+{{b}^{3}})\]
done
clear
D)
\[-2\,({{a}^{3}}+{{b}^{3}})\]
done
clear
View Answer play_arrow
question_answer 207) If \[A\left[ \begin{matrix} a & b & 0 \\ -b & a & 0 \\ 0 & 0 & 1 \\ \end{matrix} \right],\] where \[{{a}^{2}}+{{b}^{2}}=1,\] then adj is equal to
A)
\[{{A}^{-1}}\]
done
clear
B)
\[{{A}^{T}}\]
done
clear
C)
\[A\]
done
clear
D)
\[-A\] (Here, \[{{A}^{T}}\] is the transpose of A)
done
clear
View Answer play_arrow
question_answer 208) If A is a non-singular matrix such that \[{{A}^{3}}=A+I,\] then the inverse of \[B={{A}^{6}}-{{A}^{5}}\]is
A)
\[A\]
done
clear
B)
\[{{A}^{-1}}\]
done
clear
C)
\[-A\]
done
clear
D)
\[-{{A}^{-1}}\]
done
clear
View Answer play_arrow
question_answer 209) The value of \[\lambda \] such that \[x+3y+\lambda z=0,\]\[2x+4y-z=0,\,\,\,\,\,\,\,x+5y-2z=0\]has a non-trivial solution is
A)
\[-1\]
done
clear
B)
\[0\]
done
clear
C)
\[1\]
done
clear
D)
\[2\]
done
clear
View Answer play_arrow
question_answer 210) If \[A=\left[ \begin{matrix} 0 & -3 & -4/3 \\ 3 & 0 & -1/4 \\ 4/3 & 1/4 & 0 \\ \end{matrix} \right],\] then det \[(A+{{A}^{T}})\] is equal to
A)
\[0\]
done
clear
B)
\[1\]
done
clear
C)
\[2\]
done
clear
D)
\[3\]
done
clear
View Answer play_arrow
question_answer 211) If the position vector of A with respect to O is \[3\hat{i}-2\hat{j}+4\hat{k}\]and \[\overrightarrow{AB}=3\hat{i}-\hat{j}+\hat{k},\] then the position vector of B with respect to 0 is
A)
\[-\hat{j}+3\hat{k}\]
done
clear
B)
\[6\hat{i}-3\hat{j}+5\hat{k}\]
done
clear
C)
\[\hat{j}-3\hat{k}\]
done
clear
D)
\[\hat{i}-3\hat{j}+5\hat{k}\]
done
clear
View Answer play_arrow
question_answer 212) If \[|\vec{a}|=|\vec{b}|=|\vec{a}-\vec{b}|=1,\] then \[|\vec{a}+\vec{b}|\]is equal to
A)
\[1\]
done
clear
B)
\[2\]
done
clear
C)
\[\sqrt{2}\]
done
clear
D)
\[\sqrt{3}\]
done
clear
View Answer play_arrow
question_answer 213) If the vectors \[2\hat{i}-3\hat{j}+4\hat{k},\,\,\hat{i}+2\hat{j}-\hat{k}\] and \[\lambda \hat{i}-\hat{j}+2\hat{k}\]are coplanar, then X is equal to
A)
\[0\]
done
clear
B)
\[5/8\]
done
clear
C)
\[8/5\]
done
clear
D)
\[1\]
done
clear
View Answer play_arrow
question_answer 214) If \[\vec{a}=2\hat{i}+2\hat{j}+\hat{k},\,\vec{a}.\vec{b}=14\] and \[\vec{a}\times \vec{b}=3\hat{i}+\hat{j}-8\hat{k},\] then \[\vec{b}\] equals
A)
\[\hat{i}+5\hat{j}+2\hat{k}\]
done
clear
B)
\[\hat{i}-2\hat{j}+16\hat{k}\]
done
clear
C)
\[5\hat{i}+\hat{j}+2\hat{k}\]
done
clear
D)
\[5\hat{i}-\hat{j}+2\hat{k}\]
done
clear
View Answer play_arrow
question_answer 215) If \[\vec{a},\vec{b},\vec{c}\] are non-coplanar vectors and \[(\vec{a}-\lambda \vec{b}).(\vec{b}-2\vec{c})\times (\vec{c}+2\vec{a})=0,\] then \[\lambda \] is equal to
A)
\[1\]
done
clear
B)
\[1/4\]
done
clear
C)
\[0\]
done
clear
D)
\[-1/4\]
done
clear
View Answer play_arrow
question_answer 216) If \[\vec{a},\vec{b},\vec{c}\] are non-coplanar and \[[\vec{a}+\vec{b}\,\,\,\vec{b}+\vec{c}\,\,\,\,\vec{c}+\vec{a}]=k[\vec{a}\vec{b}\vec{c}],\]then k is equal to
A)
\[0\]
done
clear
B)
\[1\]
done
clear
C)
\[2\]
done
clear
D)
\[3\]
done
clear
View Answer play_arrow
question_answer 217) If \[\vec{a}+2\vec{b}+2\vec{c}=\vec{0}\] and \[(\vec{a}\times \vec{b})+(\vec{b}\times \vec{c})+(\vec{c}\times \vec{a})=\lambda (\vec{b}\times \vec{c}),\] then \[\lambda \] is equal to
A)
\[4\]
done
clear
B)
\[7\]
done
clear
C)
\[8\]
done
clear
D)
\[9\]
done
clear
View Answer play_arrow
question_answer 218) The line segment adjoining the points A , B makes projection 1,4,3 on X,Y,Z axis respectively. Then the direction cosines of AB are
A)
\[1,4,3\]
done
clear
B)
\[1/\sqrt{26},\,\,4/\sqrt{26},\,\,3/\sqrt{26}\]
done
clear
C)
\[-1/\sqrt{26},\,\,4/\sqrt{26},\,\,3/\sqrt{26}\]
done
clear
D)
\[1/\sqrt{26},-\,\,4/\sqrt{26},\,\,3/\sqrt{26}\]
done
clear
View Answer play_arrow
question_answer 219) The length of the projection of the line segment joining \[(3,-1,0)\] and \[(-3,5,\sqrt{2})\] on a line with direction cosines \[1/2,\,\,1/2,\,\,1/\sqrt{2}\] is
A)
\[1\]
done
clear
B)
\[2\]
done
clear
C)
\[3\]
done
clear
D)
\[4\]
done
clear
View Answer play_arrow
question_answer 220) The line perpendicular to the plane s\[2x-y+5z=4\] passing through the point \[(-1,0,1)\] is
A)
\[\frac{x+1}{2}=-y=\frac{z-1}{-5}\]
done
clear
B)
\[\frac{x+1}{2}=-y=\frac{z-1}{-5}\]
done
clear
C)
\[\frac{x+1}{2}=-y=\frac{z-1}{5}\]
done
clear
D)
\[\frac{x+1}{2}=y=\frac{z-1}{5}\]
done
clear
View Answer play_arrow
question_answer 221) The shortest distance between the lines \[\frac{x-2}{3}=\frac{y+3}{4}=\frac{z-1}{5}\] and \[\frac{x-5}{1}=\frac{y-1}{2}=\frac{z-6}{3}\] is
A)
\[3\]
done
clear
B)
\[2\]
done
clear
C)
\[1\]
done
clear
D)
\[0\]
done
clear
View Answer play_arrow
question_answer 222) Angle between the line \[\frac{x+1}{1}=\frac{y}{2}=\frac{z-1}{1}\] and a normal to the plane \[x-y+z=0\] is
A)
\[{{0}^{o}}\]
done
clear
B)
\[{{30}^{o}}\]
done
clear
C)
\[{{45}^{o}}\]
done
clear
D)
\[{{90}^{o}}\]
done
clear
View Answer play_arrow
question_answer 223) A point on x-axis which is equidistant from both the points \[(1,\,2,3)\] and \[(3,5,-2)\] is
A)
\[(-6,0,0)\]
done
clear
B)
\[(5,0,0)\]
done
clear
C)
\[(-5,0,0)\]
done
clear
D)
\[(6,0,0)\]
done
clear
View Answer play_arrow
question_answer 224) Foot of the perpendicular from \[(-2,1,4)\] to a plane is \[(3,1,2)\], then the equation of the plane is
A)
\[4x-2y=11\]
done
clear
B)
\[5x-2y=10\]
done
clear
C)
\[5x-2z=11\]
done
clear
D)
\[5x+2z=11\]
done
clear
View Answer play_arrow
question_answer 225) If \[\theta \] is the angle between the planes \[2x-y+z-1=0\] and \[x-2y+z+2=0,\] then \[\cos \,\theta \] is equal to
A)
\[2/3\]
done
clear
B)
\[3/4\]
done
clear
C)
\[4/5\]
done
clear
D)
\[5/6\]s
done
clear
View Answer play_arrow
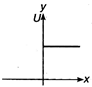
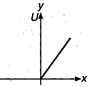
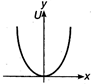
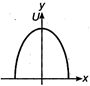
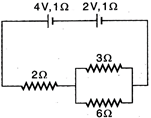
 Compound can exhibit
Compound can exhibit
