-
question_answer1)
What will be the simplified form of\[21b-32+7b-20b?\]
A)
\[21b-20b-32+7b\] done
clear
B)
\[21b-20b+7b-32\] done
clear
C)
\[8b-32\] done
clear
D)
None of the above done
clear
View Solution play_arrow
-
question_answer2)
What will be the equation form for the following statement? The sum of 3 times\[x\]and 11 is 32
A)
\[x+3\times 11=32\] done
clear
B)
\[\frac{x}{3}+11=32\] done
clear
C)
\[3(x+11)=32\] done
clear
D)
\[3x+11=32\] done
clear
View Solution play_arrow
-
question_answer3)
The statement form of the equation 5p = 20 is
A)
5 when added to p gives 20 done
clear
B)
Five times a number p is 20 done
clear
C)
Twenty times a number p is 20 done
clear
D)
None of the above done
clear
View Solution play_arrow
-
question_answer4)
Raju's father's age is 5 years more than three times Raju's age. Raju's father is 44 years old, equation to find Raju's age is:-
A)
3 (Raju's age) + 5 = 44 done
clear
B)
3 (Raju's age + 5) = 44 done
clear
C)
5 (Raju's age) + 3 = 44 done
clear
D)
Either a or b done
clear
View Solution play_arrow
-
question_answer5)
Say, whether the equation\[x+3=0\]is satisfied when\[x=3.\]
A)
Yes done
clear
B)
No done
clear
C)
Either (a) or (b) done
clear
D)
None done
clear
View Solution play_arrow
-
question_answer6)
Write an equation for the statement one-fourth of a number\[x\]minus 4 gives 4.
A)
\[\left[ \frac{1}{4}x \right]-4=4\] done
clear
B)
\[\frac{1}{4}\left[ x-4 \right]=4\] done
clear
C)
\[\frac{1}{4}-4x=4\] done
clear
D)
None done
clear
View Solution play_arrow
-
question_answer7)
Write an equation for the following statement. In an isosceles triangle, the vertex angle is twice either base angle. (Let the base angle be b in degrees).
A)
\[4b=180{}^\circ \] done
clear
B)
\[2b+c=180{}^\circ \] done
clear
C)
\[2b+2c=180{}^\circ \] done
clear
D)
None of the above done
clear
View Solution play_arrow
-
question_answer8)
The algebraic expression of the statement: ?number 5 added to three times the product of numbers m and n?.
A)
\[5mn+3\] done
clear
B)
\[2m+5n\] done
clear
C)
\[3mn+5\] done
clear
D)
None of the above done
clear
View Solution play_arrow
-
question_answer9)
Find the values of the expressions (i) \[4x-3\]and (ii) \[19-5{{x}^{2}}\] for \[x=2\]
A)
\[5,-1\] done
clear
B)
\[5,\,\,4\] done
clear
C)
\[-1,\,\,5\] done
clear
D)
\[5,\,\,1\] done
clear
View Solution play_arrow
-
question_answer10)
What should be added to\[{{x}^{2}}+xy+{{y}^{2}}\]to obtain\[2{{x}^{2}}+3xy\]?
A)
\[-{{x}^{2}}-2xy+{{y}^{2}}\] done
clear
B)
\[{{x}^{2}}-2xy-{{y}^{2}}\] done
clear
C)
\[{{x}^{2}}+2xy-{{y}^{2}}\] done
clear
D)
\[{{x}^{2}}+2xy+{{y}^{2}}\] done
clear
View Solution play_arrow
-
question_answer11)
Identify the numerical coefficients of terms (other than constants) in the following three expressions. (i) \[5-3{{t}^{2}},\] (ii) \[1+t+{{t}^{2}}+{{t}^{3}},\] (iii) \[x+2xy+3y\]
A)
\[\text{i-}-3,\,\text{ii}\,\text{-}\,1,1,1,\,iii\text{-}\,1,2,3\] done
clear
B)
\[\text{i}\,\text{-}\,\text{5},\,\text{ii}\,\text{-}\,1,1,\,iii\text{-}\,2,3\] done
clear
C)
\[\text{i}\,\text{-}\,8,\,\text{ii}\,\text{-}\,4,\,iii\text{-}\,6\] done
clear
D)
None of the above done
clear
View Solution play_arrow
-
question_answer12)
Identify the terms which give contain \[x\] and give the coefficients of\[x.\] \[{{y}^{2}}x+y\]
A)
\[{{y}^{2}},y\] done
clear
B)
\[x,\,\,1\] done
clear
C)
\[y,\,\,x\] done
clear
D)
\[{{y}^{2}}x,\,\,{{y}^{2}}\] done
clear
View Solution play_arrow
-
question_answer13)
Identify terms which contain\[{{y}^{2}}\]and give the coefficients of\[{{y}^{2}}\]in \[2{{x}^{2}}y-15x{{y}^{2}}+7{{y}^{2}}\]
A)
\[-15x{{y}^{2}},\,-15x\] done
clear
B)
\[-15x,\,7\]coefficient done
clear
C)
terms\[(-15x{{y}^{2}},-7{{y}^{2}})\]coefficient\[-15x,7\] done
clear
D)
\[2{{x}^{2}}y,-15x{{y}^{2}},7{{y}^{2}},2{{x}^{2}},-15x,7\] done
clear
View Solution play_arrow
-
question_answer14)
Classify the following expressions into monomial, binomial and trinomial. (i) \[4{{p}^{2}}q-4p{{q}^{2}}\] (ii) \[7mn\] (iii) \[1+x+{{x}^{2}}\]
A)
i - binomial, ii - monomial, iii ? trinomial done
clear
B)
i - trinomial, ii - monomial, iii - binomial done
clear
C)
i - binomial, ii - trinomial iii - monomial done
clear
D)
i - monomial, ii - binomial iii ? trinomial done
clear
View Solution play_arrow
-
question_answer15)
The area of rectangle whose length and breadth are \[4{{x}^{2}}{{y}^{3}}\] and \[2x{{y}^{2}}\] respectively is
A)
\[8{{x}^{2}}{{y}^{5}}\] done
clear
B)
\[8{{x}^{2}}{{y}^{2}}\] done
clear
C)
\[8{{x}^{3}}{{y}^{5}}\] done
clear
D)
\[6{{x}^{3}}{{y}^{5}}\] done
clear
View Solution play_arrow
-
question_answer16)
The product of monomial and monomial is always a
A)
monomial done
clear
B)
binomial done
clear
C)
trinomial done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer17)
The number of terms in the product of\[\left( 3x-2 \right)\] and\[\left( 2x+3 \right)\]is
A)
one done
clear
B)
two done
clear
C)
three done
clear
D)
four done
clear
View Solution play_arrow
-
question_answer18)
Product of \[\left( \frac{3a}{4}-\frac{2b}{3} \right)\] and \[\left( \frac{3a}{4}+\frac{2b}{3} \right)\] is
A)
\[\frac{9}{16}{{a}^{2}}-\frac{4}{9}{{b}^{2}}\] done
clear
B)
\[\frac{9}{16}{{a}^{2}}-\frac{6}{12}{{b}^{2}}\] done
clear
C)
\[\frac{9}{16}{{a}^{2}}-\frac{6}{12}{{b}^{2}}-\frac{6}{12}{{b}^{2}}-\frac{4}{9}ab\] done
clear
D)
\[\frac{6}{12}{{a}^{2}}-\frac{9}{16}{{b}^{2}}\] done
clear
View Solution play_arrow
-
question_answer19)
The highest power of the variable in a polynomial is called its
A)
degree done
clear
B)
constant done
clear
C)
like terms done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer20)
The numerical coefficient of \[{{x}^{2}}\] in the expression\[{{x}^{3}}-5{{x}^{2}}-8x+4\]
A)
\[-\]8 done
clear
B)
4 done
clear
C)
\[-\]5 done
clear
D)
1 done
clear
View Solution play_arrow
-
question_answer21)
The algebraic expression for ?Twice of\[x\]added to\[y\]squared? is
A)
\[3x+{{y}^{2}}\] done
clear
B)
\[\left( x+2 \right){{y}^{2}}\] done
clear
C)
\[\left( x+3 \right){{y}^{2}}\] done
clear
D)
\[2x+{{y}^{2}}\] done
clear
View Solution play_arrow
-
question_answer22)
Given that \[2x-5=7-x,\] then the value of\[x\]is
A)
3 done
clear
B)
4 done
clear
C)
5 done
clear
D)
1 done
clear
View Solution play_arrow
-
question_answer23)
What value of m, satisfies 17 = 3 + 2m.
A)
6 done
clear
B)
5 done
clear
C)
7 done
clear
D)
3 done
clear
View Solution play_arrow
-
question_answer24)
Divide p by 4 then add 12. If the result is 32, then the value of p is
A)
46 done
clear
B)
20 done
clear
C)
70 done
clear
D)
80 done
clear
View Solution play_arrow
-
question_answer25)
The multiplicative inverse of\[{{(16)}^{2}}\]is
A)
\[{{(16)}^{1}}\] done
clear
B)
\[{{(16)}^{-2}}\] done
clear
C)
\[{{(16)}^{-3}}\] done
clear
D)
\[1\] done
clear
View Solution play_arrow
-
question_answer26)
\[3\times 3\times 3\times 3\times 3\_\_\_200\]times can be written as
A)
\[200\times 3\] done
clear
B)
\[200+3\] done
clear
C)
\[{{(200)}^{3}}\] done
clear
D)
\[{{3}^{200}}\] done
clear
View Solution play_arrow
-
question_answer27)
Reciprocal of \[{{\left( \frac{2}{3} \right)}^{4}}\]is
A)
\[{{\left( \frac{3}{2} \right)}^{4}}\] done
clear
B)
\[{{\left( \frac{3}{2} \right)}^{-4}}\] done
clear
C)
\[{{\left( \frac{3}{2} \right)}^{3}}\] done
clear
D)
\[{{\left( \frac{3}{2} \right)}^{-3}}\] done
clear
View Solution play_arrow
-
question_answer28)
Power notation of \[\frac{36}{81}\] can be written as
A)
\[\frac{{{6}^{2}}}{{{8}^{2}}}\] done
clear
B)
\[{{\left( \frac{2}{3} \right)}^{6}}\] done
clear
C)
\[\frac{6}{9}\] done
clear
D)
\[{{\left( \frac{6}{9} \right)}^{2}}\] done
clear
View Solution play_arrow
-
question_answer29)
Exponential form of \[{{a}^{5}}\times a\times a\times {{b}^{3}}\times {{b}^{2}}\] is
A)
\[{{b}^{7}}{{a}^{5}}\] done
clear
B)
\[{{a}^{7}}{{b}^{5}}\] done
clear
C)
\[{{(ab)}^{7}}\] done
clear
D)
\[{{(ab)}^{5}}\] done
clear
View Solution play_arrow
-
question_answer30)
Simplest form of \[{{\left( \frac{4}{9} \right)}^{3/2}}\]is
A)
\[{{\left( \frac{9}{4} \right)}^{2/3}}\] done
clear
B)
\[\frac{8}{27}\] done
clear
C)
\[\frac{27}{8}\] done
clear
D)
\[{{\left( \frac{8}{27} \right)}^{2}}\] done
clear
View Solution play_arrow
-
question_answer31)
Value of expression\[{{(8)}^{2/3}}+{{4}^{3/2}}\]is
A)
12 done
clear
B)
18 done
clear
C)
10 done
clear
D)
14 done
clear
View Solution play_arrow
-
question_answer32)
Exponential form of \[16\times 27\times 81\]is
A)
\[{{2}^{4}}\times {{3}^{3}}\times {{8}^{1}}\] done
clear
B)
\[{{2}^{7}}\times {{3}^{4}}\] done
clear
C)
\[{{2}^{4}}\times {{3}^{4}}\times {{3}^{4}}\] done
clear
D)
\[{{2}^{4}}\times {{3}^{7}}\] done
clear
View Solution play_arrow
-
question_answer33)
Evaluate: \[{{\left( \frac{2}{7} \right)}^{\frac{1}{2}}}\times {{\left( \frac{2}{7} \right)}^{\frac{3}{2}}}\]
A)
\[{{\left( \frac{2}{7} \right)}^{\frac{3}{4}}}\] done
clear
B)
\[{{\left( \frac{2}{7} \right)}^{-1}}\] done
clear
C)
\[\frac{4}{49}\] done
clear
D)
\[\frac{49}{4}\] done
clear
View Solution play_arrow
-
question_answer34)
\[{{\text{3}}^{x}}=243,\]then\[x\]is equal to
A)
4 done
clear
B)
6 done
clear
C)
5 done
clear
D)
7 done
clear
View Solution play_arrow
-
question_answer35)
Simple form of \[{{(-3)}^{2}}\times {{(-2)}^{3}}\] is
A)
\[-72\] done
clear
B)
\[-24\] done
clear
C)
\[72\] done
clear
D)
\[18\] done
clear
View Solution play_arrow
-
question_answer36)
The value of \[{{\left( \frac{-2}{3} \right)}^{7}}\]is
A)
negative done
clear
B)
0 done
clear
C)
positive done
clear
D)
none of these done
clear
View Solution play_arrow
-
question_answer37)
\[{{\left( \frac{1}{3} \right)}^{7}}\div {{\left( \frac{-1}{3} \right)}^{4}}\]is equal to
A)
\[{{\left( \frac{1}{3} \right)}^{11}}\] done
clear
B)
\[{{\left( \frac{1}{3} \right)}^{3}}\] done
clear
C)
\[{{\left( \frac{1}{3} \right)}^{-3}}\] done
clear
D)
\[1\] done
clear
View Solution play_arrow
-
question_answer38)
Standard form of 7000000 is
A)
\[7.0\times {{10}^{6}}\] done
clear
B)
\[0.7\times {{10}^{7}}\] done
clear
C)
\[70\times {{10}^{5}}\] done
clear
D)
\[70\times {{10}^{6}}\] done
clear
View Solution play_arrow
-
question_answer39)
DIRECTIONS: Match Column-I with Column-II and select the correct answer using the codes given below the columns. For any two rational numbers a and b and for any integers m and n, match the laws of exponents given in Column - I with Column - II.
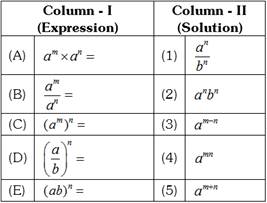
A B C D E
A)
3 5 2 4 1 done
clear
B)
5 3 4 1 2 done
clear
C)
5 3 1 4 2 done
clear
D)
3 5 4 2 1 done
clear
View Solution play_arrow
-
question_answer40)
DIRECTIONS: Match Column-I with Column-II and select the correct answer using the codes given below the columns.
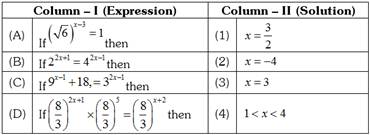
A B C D
A)
1 2 3 4 done
clear
B)
3 4 2 1 done
clear
C)
3 1 4 2 done
clear
D)
1 2 4 3 done
clear
View Solution play_arrow
-
question_answer41)
DIRECTIONS: Match Column-I with Column-II and select the correct answer using the codes given below the columns.

A B C D
A)
3 4 1 2 done
clear
B)
3 1 4 2 done
clear
C)
2 3 1 4 done
clear
D)
4 3 1 2 done
clear
View Solution play_arrow
-
question_answer42)
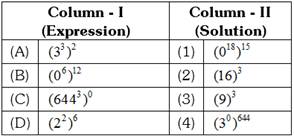
A B C D
A)
3 1 2 4 done
clear
B)
3 1 4 2 done
clear
C)
1 2 3 4 done
clear
D)
1 3 2 4 done
clear
View Solution play_arrow
-
question_answer43)
Consider the following statements. (i) If there is only one term in an expression, it is called a monomial. (ii) An algebraic expression is a combination of numbers, literals, and arithmetic operations. (iii) An algebraic expression with one or more terms is also referred to as a polynomial. Which of the statement(s) is/are true
A)
Only (i) done
clear
B)
Only (ii) done
clear
C)
Only (iii) done
clear
D)
All of the above done
clear
View Solution play_arrow
-
question_answer44)
Consider the following statements. Statement A: Like terms of an algebraic expression can be added or subtracted. Statement B: Unlike terms cannot be added or subtracted to get a new term.
A)
Only statement A is correct done
clear
B)
Only statement B is correct done
clear
C)
Either statement A or statement B is correct done
clear
D)
Both the statements are correct. done
clear
View Solution play_arrow
-
question_answer45)
Read the following statements. (i) \[2{{a}^{2}}+a-5,3{{x}^{2}}+2,3{{y}^{2}}\]are all polynomials of the second degree. (ii) \[4{{x}^{3}}+3,6{{a}^{3}}+4{{a}^{2}}+2a+1,\]and\[4{{m}^{3}}\]are all polynomials of the third degree. (iii) The term with the highest power in a polynomial decides the degree of the polynomial. Which of the statement(s) is/are correct?
A)
only (i) and (ii) done
clear
B)
only (ii) and (iii) done
clear
C)
only (i) and (iii) done
clear
D)
(i),(ii) and (iii) done
clear
View Solution play_arrow
-
question_answer46)
Consider the following statement. (i) To solve an equation means to find the value of the unknown variable in the equation. (ii) Value of the unknown variable is called the root of the equation. (iii) All monomials, binomials, trinomials, and polynomials are called by the name polynomial. Which of the statement (s) is/are true?
A)
(i), (ii) and (iii) done
clear
B)
(i) and (ii) done
clear
C)
(i) and (iii) done
clear
D)
(ii) and (iii) done
clear
View Solution play_arrow
-
question_answer47)
Consider the following statements. (i) \[\sqrt{2x}+6{{x}^{2}}+7\]is a polynomial of degree 2. (ii) \[4{{e}^{2}}+\frac{1}{6}e+2\sqrt{4}\]is not a polynomial. (iii) \[8{{a}^{3}}{{b}^{2}}-4{{a}^{2}}b+6ab-3\] is a polynomial of degree 5. Which of the statement(s) is incorrect?
A)
only (i) and (ii) done
clear
B)
only (i) and (iii) done
clear
C)
only (ii) and (iii) done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer48)
Consider the following algebraic identities. (i) \[{{(a+b)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}\] (ii) \[{{(a-b)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}\] (iii) \[{{a}^{2}}-{{b}^{2}}=(a-b)\,(a+b)\] (iv) \[(a+x)(a+y)={{a}^{2}}+a(x+y)+xy\] Which of the identity is/are incorrect?
A)
only (i), (ii) and (iii) done
clear
B)
only (i), (iii) and (iv) done
clear
C)
only (ii), (iii) and (iv) done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer49)
DIRECTIONS: Passage ? 1 Read the passage(s) given below and answer the questions that follow. Let K represents any terminating decimal or a number from 1 to 9.999 _ _ _ (or\[1\le K<10\]). Then we can express very large and very small numbers in special form such as \[K\times {{10}^{n}},\] where n is any integer. This form of writing numbers is known as scientific notation. This form of numbers is also called the standard form. Scientific notation 0.23 is
A)
\[2.3\times {{10}^{-1}}\] done
clear
B)
\[2.3\] done
clear
C)
\[2.3\times 10\] done
clear
D)
\[\frac{2.3}{10}\] done
clear
View Solution play_arrow
-
question_answer50)
DIRECTIONS: Passage ? 1 Read the passage(s) given below and answer the questions that follow. Let K represents any terminating decimal or a number from 1 to 9.999 _ _ _ (or\[1\le K<10\]). Then we can express very large and very small numbers in special form such as \[K\times {{10}^{n}},\] where n is any integer. This form of writing numbers is known as scientific notation. This form of numbers is also called the standard form. Scientific notation of .0000072 is
A)
\[7.2\times {{10}^{-7}}\] done
clear
B)
\[7.2\times {{10}^{7}}\] done
clear
C)
\[7.2\times {{10}^{-6}}\] done
clear
D)
\[72\times {{10}^{-6}}\] done
clear
View Solution play_arrow
-
question_answer51)
DIRECTIONS: Passage ? 1 Read the passage(s) given below and answer the questions that follow. Let K represents any terminating decimal or a number from 1 to 9.999 _ _ _ (or\[1\le K<10\]). Then we can express very large and very small numbers in special form such as \[K\times {{10}^{n}},\] where n is any integer. This form of writing numbers is known as scientific notation. This form of numbers is also called the standard form. Usual form of \[1.05\times {{10}^{3}}\]is
A)
105 done
clear
B)
1050 done
clear
C)
10500 done
clear
D)
105000 done
clear
View Solution play_arrow
-
question_answer52)
DIRECTIONS: The questions in this segment consists of two statements, one labelled as ?Assertion A? and the other labelled as ?Reason R?. You are to examine these two statements carefully and decide if the Assertion A and Reason R are individually true and if so, whether the reason is a correct explanation of the assertion. Select your answers to these items using codes given below. Assertion (A): 2a + 3b + c is a trinomial Reason (R): An algebraic expression which contains only three terms is called trinomial.
A)
If both Assertion and Reason are correct and Reason is the correct explanation of Assertion. done
clear
B)
If both Assertion and Reason are correct, but Reason is not the correct explanation of Assertion. done
clear
C)
If Assertion is correct but Reason is incorrect. done
clear
D)
If Assertion is incorrect but Reason is correct. done
clear
View Solution play_arrow
-
question_answer53)
DIRECTIONS: The questions in this segment consists of two statements, one labelled as ?Assertion A? and the other labelled as ?Reason R?. You are to examine these two statements carefully and decide if the Assertion A and Reason R are individually true and if so, whether the reason is a correct explanation of the assertion. Select your answers to these items using codes given below. Assertion (A): The degree of \[x+{{x}^{2}}-3{{x}^{4}}+1\] is 4. Reason (R): The term with the highest power in a polynomial decides the degree of the polynomial.
A)
If both Assertion and Reason are correct and Reason is the correct explanation of Assertion. done
clear
B)
If both Assertion and Reason are correct, but Reason is not the correct explanation of Assertion. done
clear
C)
If Assertion is correct but Reason is incorrect. done
clear
D)
If Assertion is incorrect but Reason is correct. done
clear
View Solution play_arrow
-
question_answer54)
DIRECTIONS: The questions in this segment consists of two statements, one labelled as ?Assertion A? and the other labelled as ?Reason R?. You are to examine these two statements carefully and decide if the Assertion A and Reason R are individually true and if so, whether the reason is a correct explanation of the assertion. Select your answers to these items using codes given below. Assertion (A): Value of \[{{\left( \frac{4}{9} \right)}^{\frac{3}{2}}}\times {{\left( \frac{4}{9} \right)}^{\frac{1}{2}}}\]is \[{{\left( \frac{4}{9} \right)}^{2}}.\] Reason (R): For any two rational numbers a and b and for any integers m and n, we have \[{{a}^{m}}\times {{a}^{n}}={{a}^{m+n}}\]
A)
If both Assertion and Reason are correct and Reason is the correct explanation of Assertion. done
clear
B)
If both Assertion and Reason are correct, but Reason is not the correct explanation of Assertion. done
clear
C)
If Assertion is correct but Reason is incorrect. done
clear
D)
If Assertion is incorrect but Reason is correct. done
clear
View Solution play_arrow
-
question_answer55)
DIRECTIONS: The questions in this segment consists of two statements, one labelled as ?Assertion A? and the other labelled as ?Reason R?. You are to examine these two statements carefully and decide if the Assertion A and Reason R are individually true and if so, whether the reason is a correct explanation of the assertion. Select your answers to these items using codes given below. Assertion (A): Value of \[{{(27)}^{\frac{6}{5}}}\div {{(27)}^{\frac{1}{5}}}\] is \[1\times {{3}^{3}}\] Reason (R): For any two rational numbers a and b and for any integers m and n, we have\[{{a}^{m}}\div {{a}^{n}}={{a}^{m-n}}\]
A)
If both Assertion and Reason are correct and Reason is the correct explanation of Assertion. done
clear
B)
If both Assertion and Reason are correct, but Reason is not the correct explanation of Assertion. done
clear
C)
If Assertion is correct but Reason is incorrect. done
clear
D)
If Assertion is incorrect but Reason is correct. done
clear
View Solution play_arrow
-
question_answer56)
DIRECTIONS: The questions in this segment consists of two statements, one labelled as ?Assertion A? and the other labelled as ?Reason R?. You are to examine these two statements carefully and decide if the Assertion A and Reason R are individually true and if so, whether the reason is a correct explanation of the assertion. Select your answers to these items using codes given below. Assertion (A): Value of \[{{\left[ {{(729)}^{-\frac{5}{3}}} \right]}^{-\frac{1}{2}}}\]is 243. Reason (R): For any two rational numbers a and b and for any integers m and n, we have\[{{(ab)}^{n}}={{a}^{n}}.{{b}^{n}}\]
A)
If both Assertion and Reason are correct and Reason is the correct explanation of Assertion. done
clear
B)
If both Assertion and Reason are correct, but Reason is not the correct explanation of Assertion. done
clear
C)
If Assertion is correct but Reason is incorrect. done
clear
D)
If Assertion is incorrect but Reason is correct. done
clear
View Solution play_arrow
-
question_answer57)
Identify the like terms in the following (i) \[-x{{y}^{2}},\] (ii) \[-4y{{x}^{2}},\] (iii) \[8{{x}^{2}},\](iv) \[2x{{y}^{2}},\] (v) \[7y,\] (vi) \[-11{{x}^{2}},\](vii) \[-100x,\](viii) \[-11yx,\] (ix) \[20{{x}^{2}}y\]
A)
(i) and (iv) done
clear
B)
(ii) and (vi) done
clear
C)
Both a & b done
clear
D)
None done
clear
View Solution play_arrow
-
question_answer58)
If \[m=2,\] the value of \[\frac{5m}{2}-4\]
A)
\[2\] done
clear
B)
\[10\] done
clear
C)
\[\frac{5}{2}\] done
clear
D)
\[1\] done
clear
View Solution play_arrow
-
question_answer59)
If \[p=-2,\] the value of\[-2{{p}^{3}}-3{{p}^{2}}+4p+7\]
A)
\[0\] done
clear
B)
\[1\] done
clear
C)
\[3\] done
clear
D)
\[-3\] done
clear
View Solution play_arrow
-
question_answer60)
Find the value of the expression \[{{x}^{2}}+2x+1\] when\[x=-1\]
A)
\[1\] done
clear
B)
\[0\] done
clear
C)
\[2\] done
clear
D)
\[-1\] done
clear
View Solution play_arrow
-
question_answer61)
In\[6\left( 2a-1 \right)+8=14,\]the value of \['a'\] is
A)
\[-1\] done
clear
B)
\[3\frac{1}{12}\] done
clear
C)
\[1\frac{3}{12}\] done
clear
D)
\[+1\] done
clear
View Solution play_arrow
-
question_answer62)
The solution of\[0.2(2x-1)-0.5(3x-1)=0.4\]is
A)
\[\frac{1}{11}\] done
clear
B)
\[-\frac{1}{11}\] done
clear
C)
\[\frac{3}{11}\] done
clear
D)
\[\frac{-3}{11}\] done
clear
View Solution play_arrow
-
question_answer63)
If 20% of 60% of a number is 144, then the number is
A)
1200 done
clear
B)
2880 done
clear
C)
8640 done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer64)
The ratio of two numbers is a : b. If one of them is x, then other is
A)
\[\frac{ab}{x}\] done
clear
B)
\[\frac{b}{ax}\] done
clear
C)
\[\frac{b}{a+b}x\] done
clear
D)
\[\frac{bx}{a}\] done
clear
View Solution play_arrow
-
question_answer65)
Which of the following expressions is a polynomial?
A)
\[3{{x}^{\frac{1}{2}}}-4x+3\] done
clear
B)
\[4{{x}^{2}}-3\sqrt{x}+5\] done
clear
C)
\[3{{x}^{2}}y-2xy+5{{x}^{4}}\] done
clear
D)
\[2{{x}^{4}}+\frac{3}{{{x}^{2}}}-1\] done
clear
View Solution play_arrow
-
question_answer66)
The value of \[25{{x}^{2}}+16{{y}^{2}}+40xy\] at \[x=1\] and \[y=-1\]is
A)
81 done
clear
B)
\[-49\] done
clear
C)
1 done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer67)
\[\left( 3A+B \right)-3\left( A-B \right)\]equals
A)
\[4A\] done
clear
B)
\[4B\] done
clear
C)
\[2A+2B\] done
clear
D)
\[4A-2B\] done
clear
View Solution play_arrow
-
question_answer68)
\[{{x}^{2}}-{{(-x)}^{2}}\]is equal to
A)
\[-2{{x}^{2}}\] done
clear
B)
\[2{{x}^{2}}\] done
clear
C)
\[{{x}^{4}}\] done
clear
D)
\[0\] done
clear
View Solution play_arrow
-
question_answer69)
What should be added to\[-3p+7q-16\] to get the sum 8?
A)
\[8\] done
clear
B)
\[-3p+7q+8\] done
clear
C)
\[3p-7q+8\] done
clear
D)
\[3p-7q+24\] done
clear
View Solution play_arrow
-
question_answer70)
If \[5x+2=5,\] then\[x\]equals
A)
\[\frac{4}{5}\] done
clear
B)
\[\frac{2}{5}\] done
clear
C)
\[\frac{3}{5}\] done
clear
D)
\[\frac{6}{5}\] done
clear
View Solution play_arrow
-
question_answer71)
What value of \[y\] would make expressions \[4y+5\] and\[-y+15\]equal?
A)
\[1\] done
clear
B)
\[-2\] done
clear
C)
\[2\] done
clear
D)
\[1\] done
clear
View Solution play_arrow
-
question_answer72)
The value of \[{{a}^{2}}+{{b}^{2}}+{{c}^{2}}-ab+bc-ac+a\]for\[a=1,b=2\] and \[c=-1\] is
A)
2 done
clear
B)
4 done
clear
C)
7 done
clear
D)
5 done
clear
View Solution play_arrow
-
question_answer73)
On solving \[\left( x-y \right)\left( x+y \right)+\left( y-z \right)\left( y+z \right)+\left( z-x \right)\left( z+x \right)\]
A)
\[0\] done
clear
B)
\[1\] done
clear
C)
\[-1\] done
clear
D)
\[2\] done
clear
View Solution play_arrow
-
question_answer74)
DIRECTIONS: Match Column-I with Column-II and select the correct answer using the codes given below the columns. Match the like terms in the Column-I and Column-II and select correct option from the options given below:
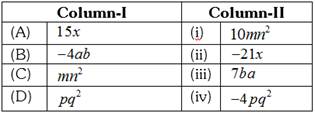
A)
\[\text{A-}\,\text{ii},B\text{-}\,\text{iii},C\text{-}i,D\,\text{-}iv\] done
clear
B)
\[\text{A-}\,\text{i},B\text{-}\,\text{iii},C\text{-}ii,D\,\text{-}iv\] done
clear
C)
\[\text{A-}\,\text{iii},B\text{-}\,\text{ii},C\text{-}iv,D\,\text{-}i\] done
clear
D)
\[\text{A-}\,\text{i},B\text{-}\,\text{ii},C\text{-}iii,D\,\text{-}iv\] done
clear
View Solution play_arrow
-
question_answer75)
DIRECTIONS: Match Column-I with Column-II and select the correct answer using the codes given below the columns.
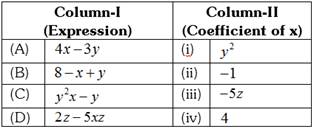
A)
\[\text{A}\,\text{-}\,\text{s,}\,\text{B}\,\text{-}\,\text{r,}\,\text{C}\,\text{-}\,\text{p,}\,\text{D}\,\text{-}\,\text{q}\] done
clear
B)
\[\text{A}\,\text{-}\,\text{p,}\,\text{B}\,\text{-}\,\text{q,}\,\text{C}\,\text{-}\,\text{r,}\,\text{D}\,\text{-}\,\text{s}\] done
clear
C)
\[\text{A}\,\text{-}\,\text{s,}\,\text{B}\,\text{-}\,\text{q,}\,\text{C}\,\text{-}\,\text{p,}\,\text{D}\,\text{-}\,\text{r}\] done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer76)
DIRECTIONS: Match Column-I with Column-II and select the correct answer using the codes given below the columns.
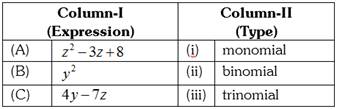
A)
\[\text{A}\,\text{-}\,\text{r,}\,\text{B}\,\text{-}\,\text{p,}\,\text{C}\,\text{-}\,\text{q}\] done
clear
B)
\[\text{A}\,\text{-}\,\text{q,}\,\text{B}\,\text{-}\,\text{r,}\,\text{C}\,\text{-}\,\text{p}\] done
clear
C)
\[\text{A}\,\text{-}\,\text{p,}\,\text{B}\,\text{-}\,\text{q,}\,\text{C}\,\text{-}\,\text{r}\] done
clear
D)
\[\text{A}\,\text{-}\,\text{r,}\,\text{B}\,\text{-}\,\text{q,}\,\text{C}\,\text{-}\,\text{p}\] done
clear
View Solution play_arrow
-
question_answer77)
DIRECTIONS: Match Column-I with Column-II and select the correct answer using the codes given below the columns.
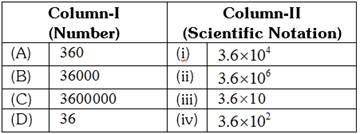
A B C D
A)
1 2 3 4 done
clear
B)
1 4 2 3 done
clear
C)
4 1 3 2 done
clear
D)
4 1 2 3 done
clear
View Solution play_arrow
-
question_answer78)
DIRECTIONS: Match Column-I with Column-II and select the correct answer using the codes given below the columns.

A B C D
A)
2 1 4 3 done
clear
B)
2 1 3 4 done
clear
C)
1 2 3 4 done
clear
D)
1 2 4 3 done
clear
View Solution play_arrow
-
question_answer79)
DIRECTIONS: Match Column-I with Column-II and select the correct answer using the codes given below the columns.
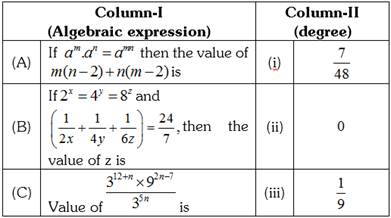
A)
\[A\to 3;B\to 2;C\to 1\] done
clear
B)
\[A\to 2;B\to 1;C\to 3\] done
clear
C)
\[A\to 1;B\to 2;C\to 3\] done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer80)
DIRECTIONS: Match Column-I with Column-II and select the correct answer using the codes given below the columns.
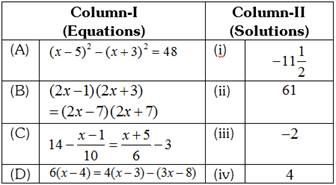
A B C D
A)
1 2 3 4 done
clear
B)
3 1 4 2 done
clear
C)
2 1 3 4 done
clear
D)
3 1 2 4 done
clear
View Solution play_arrow
-
question_answer81)
Consider the following statements: (i) The value of\[{{\left( 5x-3y \right)}^{2}}-{{\left( 5x+3y \right)}^{2}}\]when\[x=-1\]and\[y=\frac{1}{5}\]is 12. (ii) Algebraic identity used to solve \[{{\left( 25.732 \right)}^{2}}-{{\left( 15.732 \right)}^{2}}\]is \[\left( a-b \right)\left( a+b \right)\] (iii) Value of\[\left( x+4 \right)\left( x-4 \right)\left( {{x}^{2}}+16 \right)\]is\[{{x}^{2}}-64.\] Which of the above statement is/are true?
A)
only (i) and (iii) done
clear
B)
only (ii) and (iii) done
clear
C)
only (i) and (ii) done
clear
D)
(i), (ii) and (iii) done
clear
View Solution play_arrow
-
question_answer82)
For which equation(s) is \[x=3\]a solution? (i) \[2x-5+3x=10\] (ii) \[\frac{-x+7}{2}=2\] (iii) \[4x-11=17\] (iv) \[9=-(x-1)+11\]
A)
only (i) done
clear
B)
(i) and (ii) done
clear
C)
(i), (ii) and (iii) done
clear
D)
(i), (ii) and (iv) done
clear
View Solution play_arrow
-
question_answer83)
Consider the statements given below. (i) If we fail to do the same mathematical operation on both sides of an equality, the equality does not hold. (ii) The value of the variable for which the equation is satisfied is called the solution of the equation. (iii) When we add two algebraic expressions, the unlike terms are added (iv) All monomials, binomials, trinomials and polynomials are called by the name algebraic expressions. Which of the above statements is/are incorrect?
A)
only (i) done
clear
B)
only (ii) done
clear
C)
only (iii) done
clear
D)
only (iv) done
clear
View Solution play_arrow
-
question_answer84)
DIRECTIONS: The questions in this segment consists of two statements, one labelled as ?Assertion A? and the other labelled as ?Reason R?. You are to examine these two statements carefully and decide if the Assertion A and Reason R are individually true and if so, whether the reason is a correct explanation of the assertion. Select your answers to these items using codes given below. Assertion (A): Value of \[x\] in expression \[3x+3=15-3\] is 3. Reason (R): Variable \[x\] represent maximum times in this expression.
A)
If both Assertion and Reason are correct and Reason is the correct explanation of Assertion. done
clear
B)
If both Assertion and Reason are correct, but Reason is not the correct explanation of Assertion. done
clear
C)
If Assertion is correct but Reason is incorrect. done
clear
D)
If Assertion is incorrect but Reason is correct. done
clear
View Solution play_arrow
-
question_answer85)
DIRECTIONS: The questions in this segment consists of two statements, one labelled as ?Assertion A? and the other labelled as ?Reason R?. You are to examine these two statements carefully and decide if the Assertion A and Reason R are individually true and if so, whether the reason is a correct explanation of the assertion. Select your answers to these items using codes given below. Assertion (A): An equation changes if the L.H.S. and R.H.S. are interchanged. Reason (R): Algebraic expression must contain at least one variable.
A)
If both Assertion and Reason are correct and Reason is the correct explanation of Assertion. done
clear
B)
If both Assertion and Reason are correct, but Reason is not the correct explanation of Assertion. done
clear
C)
If Assertion is correct but Reason is incorrect. done
clear
D)
If Assertion is incorrect but Reason is correct. done
clear
View Solution play_arrow
-
question_answer86)
DIRECTIONS: The questions in this segment consists of two statements, one labelled as ?Assertion A? and the other labelled as ?Reason R?. You are to examine these two statements carefully and decide if the Assertion A and Reason R are individually true and if so, whether the reason is a correct explanation of the assertion. Select your answers to these items using codes given below. Assertion (A): \[3-t>2\] is an in equation. Reason (R): For \[t=0\] and \[1,\,\,3-t>2.\]
A)
If both Assertion and Reason are correct and Reason is the correct explanation of Assertion. done
clear
B)
If both Assertion and Reason are correct, but Reason is not the correct explanation of Assertion. done
clear
C)
If Assertion is correct but Reason is incorrect. done
clear
D)
If Assertion is incorrect but Reason is correct. done
clear
View Solution play_arrow
-
question_answer87)
DIRECTIONS: The questions in this segment consists of two statements, one labelled as ?Assertion A? and the other labelled as ?Reason R?. You are to examine these two statements carefully and decide if the Assertion A and Reason R are individually true and if so, whether the reason is a correct explanation of the assertion. Select your answers to these items using codes given below. Assertion A: \[x+y\] and \[2m+\text{2}n\] cannot be added to give a 2 term expression. Reason R: All the four terms are unlike.
A)
If both Assertion and Reason are correct and Reason is the correct explanation of Assertion. done
clear
B)
If both Assertion and Reason are correct, but Reason is not the correct explanation of Assertion. done
clear
C)
If Assertion is correct but Reason is incorrect. done
clear
D)
If Assertion is incorrect but Reason is correct. done
clear
View Solution play_arrow
-
question_answer88)
DIRECTIONS: The questions in this segment consists of two statements, one labelled as ?Assertion A? and the other labelled as ?Reason R?. You are to examine these two statements carefully and decide if the Assertion A and Reason R are individually true and if so, whether the reason is a correct explanation of the assertion. Select your answers to these items using codes given below. Assertion A: 5 is added to both sides of the equation \[x+a=b\] but the value of the equation doesn't change. Reason R: If we perform the same mathematical operation on both sides of the equation its value doesn't change.
A)
If both Assertion and Reason are correct and Reason is the correct explanation of Assertion. done
clear
B)
If both Assertion and Reason are correct, but Reason is not the correct explanation of Assertion. done
clear
C)
If Assertion is correct but Reason is incorrect. done
clear
D)
If Assertion is incorrect but Reason is correct. done
clear
View Solution play_arrow
-
question_answer89)
DIRECTIONS: The questions in this segment consists of two statements, one labelled as ?Assertion A? and the other labelled as ?Reason R?. You are to examine these two statements carefully and decide if the Assertion A and Reason R are individually true and if so, whether the reason is a correct explanation of the assertion. Select your answers to these items using codes given below. Assertion (A): The solution of the equation \[\frac{x}{2}+\frac{1}{2}=\frac{x}{3}-\frac{1}{3}\] represents an integer which is between\[0\]and\[-10.\] Reason (R): The solution of the equation \[2\left( 3x-7 \right)+4\left( 3x+2 \right)=6\left( 5x+9 \right)+3\] is a rational number.
A)
If both Assertion and Reason are correct and Reason is the correct explanation of Assertion. done
clear
B)
If both Assertion and Reason are correct, but Reason is not the correct explanation of Assertion. done
clear
C)
If Assertion is correct but Reason is incorrect. done
clear
D)
If Assertion is incorrect but Reason is correct. done
clear
View Solution play_arrow
-
question_answer90)
DIRECTIONS: The questions in this segment consists of two statements, one labelled as ?Assertion A? and the other labelled as ?Reason R?. You are to examine these two statements carefully and decide if the Assertion A and Reason R are individually true and if so, whether the reason is a correct explanation of the assertion. Select your answers to these items using codes given below. Assertion (A): Value of \[\frac{{{2}^{x+3}}\times {{3}^{2x-y}}\times {{5}^{x+y+3}}\times {{6}^{y+1}}}{{{6}^{x+1}}\times {{10}^{y+3}}\times {{15}^{x}}}\] Reason: Value of x so that \[x={{(64)}^{\sqrt{-\frac{1}{2}}}}-{{(-32)}^{-\frac{4}{5}}}\]is \[\frac{3}{6}\]
A)
If both Assertion and Reason are correct and Reason is the correct explanation of Assertion. done
clear
B)
If both Assertion and Reason are correct, but Reason is not the correct explanation of Assertion. done
clear
C)
If Assertion is correct but Reason is incorrect. done
clear
D)
If Assertion is incorrect but Reason is correct. done
clear
View Solution play_arrow
