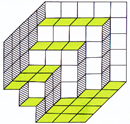
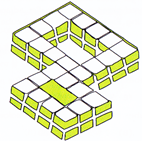
![]()
![]()
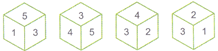
 done
clear
done
clear
 done
clear
done
clear
 done
clear
done
clear
 done
clear
done
clear
![]()
You need to login to perform this action.
You will be redirected in
3 sec
