10th Class Mathematics Introduction to Trigonometry Question Bank

done Trigonometry Total Questions - 206

• question_answer1)
  The value of \[36{}^\circ \] in radians is
  A)
  \[\frac{\pi }{2}\] done clear
  B)
  \[\frac{2pi }{5}\] done clear
  C)
  \[\frac{\pi }{5}\] done clear
  D)
  \[3\pi \] done clear
  View Solution play_arrow

• question_answer2)
  Which one of the following is correct?
  A)
  \[{{\sec }^{2}}\alpha =1-{{\tan }^{2}}\alpha \] done clear
  B)
  \[{{\sin }^{2}}\alpha =1+{{\cos }^{2}}\alpha \] done clear
  C)
  \[\tan \,\alpha \,\,\cot =1\] done clear
  D)
  None of these done clear
  View Solution play_arrow

• question_answer3)
  Which one of the following is true?
  A)
  \[\sin (90{}^\circ -\theta )=sin\theta \] done clear
  B)
  \[cos(90{}^\circ -\theta )=\cos \theta \] done clear
  C)
  \[\sin (90{}^\circ -\theta )=\cos \theta \] done clear
  D)
  \[tan(90{}^\circ +\theta )=\tan \theta \] done clear
  View Solution play_arrow

• question_answer4)
  The value of \[\sin B\,(90{}^\circ -B)+cos\,B\,\,sin(90{}^\circ -B)\] is
  A)
  0 done clear
  B)
  1 done clear
  C)
  \[\text{sinB}\,\,\text{cos}\,\text{B}\] done clear
  D)
  \[2\,\,{{\sin }^{2}}B\] done clear
  View Solution play_arrow

• question_answer5)
  The maximum value of \[\sin \theta +\cos \theta \] is
  A)
  1 done clear
  B)
  2 done clear
  C)
  3 done clear
  D)
  \[\sqrt{2}\] done clear
  View Solution play_arrow

• question_answer6)
  If \[\alpha +\beta =\frac{\pi }{2}\] and \[\alpha =\frac{1}{3}\], then sin \[\beta \] is equal to
  A)
  \[\frac{\sqrt{2}}{3}\] done clear
  B)
  \[\frac{2\sqrt{2}}{3}\] done clear
  C)
  \[\frac{2}{3}\] done clear
  D)
  \[\frac{3}{4}\] done clear
  View Solution play_arrow

• question_answer7)
  If  \[5\tan \theta =4\], then value of \[\frac{5\sin \theta -3\,\,\cos \theta }{5\sin \theta +2\,\,\cos \theta }\] is
  A)
  \[\frac{1}{3}\] done clear
  B)
  \[\frac{1}{6}\] done clear
  C)
  \[\frac{4}{5}\] done clear
  D)
  \[\frac{3}{2}\] done clear
  View Solution play_arrow

• question_answer8)
  If in a \[\Delta ABC\] m \[\angle A=\frac{\pi }{2}\], then value of \[{{\cos }^{2}}\,A+{{\cos }^{2}}B+{{\cos }^{2}}C\] is
  A)
  3 done clear
  B)
  2 done clear
  C)
  \[\frac{3}{2}\] done clear
  D)
  1 done clear
  View Solution play_arrow

• question_answer9)
  If \[0{}^\circ <x<45{}^\circ \], then consider the following statements:  

  Assertion (A):\[\frac{1}{1+{{\sin }^{2}}x}-\frac{1}{1+{{\sec }^{2}}x}\ne \frac{1}{1+{{\cos }^{2}}x}-\frac{1}{1+\text{cose}{{\text{c}}^{2}}x}\]

  Reason (R): \[\sin x\ne \cos x\]

    Of these statements:
  A)
   Both A and II are true and R is the correct explanation of A   done clear
  B)
   Both A and R are true, but R is not the correct explanation of A. done clear
  C)
   A is true, but R is false. done clear
  D)
   A is false, but R is true. done clear
  View Solution play_arrow

• question_answer10)
  The value of \[{{\cos }^{4}}\theta +{{\sin }^{4}}\theta +2{{\cos }^{2}}\theta {{\sin }^{2}}\theta \] when \[\theta =45{}^\circ \] is
  A)
  1 done clear
  B)
  2 done clear
  C)
  \[\frac{1}{\sqrt{2}}\] done clear
  D)
  \[2\sqrt{2}\] done clear
  View Solution play_arrow

• question_answer11)
  On simplifying \[\frac{1}{\text{cosec}\theta +\text{cot}\theta }\] , two students got the following answers :  

  I. \[\text{cosec}\theta -\text{cot}\theta \]

  II. \[\frac{1}{\text{cosec}\theta +\text{cot}\theta }\]

    Of these answers
  A)
  both I and II are correct done clear
  B)
  both are wrong done clear
  C)
  I is wrong, II is correct done clear
  D)
  I is correct, I is wrong done clear
  View Solution play_arrow

• question_answer12)
  If \[\tan \,\,\theta =\frac{1}{\sqrt{5}}\] and \[\theta \] lies in the first quadrant, the value of \[\cos \,\theta \] is
  A)
  \[\frac{1}{\sqrt{6}}\] done clear
  B)
  \[\frac{\sqrt{5}}{\sqrt{6}}\] done clear
  C)
  \[-\frac{1}{\sqrt{6}}\] done clear
  D)
  \[-\frac{\sqrt{5}}{\sqrt{6}}\] done clear
  View Solution play_arrow

• question_answer13)
  The value of \[\sin 50{}^\circ -\sin 70{}^\circ +\sin 10{}^\circ \] is
  A)
  1 done clear
  B)
  2 done clear
  C)
  -1 done clear
  D)
  0 done clear
  View Solution play_arrow

• question_answer14)
  The value of \[cos25{}^\circ \cos 20{}^\circ +\sin 25{}^\circ \sin 20{}^\circ \] is
  A)
  \[\frac{1}{\sqrt{2}}\] done clear
  B)
  \[2\] done clear
  C)
  \[cos\,5{}^\circ \] done clear
  D)
  \[\sin \,5{}^\circ \] done clear
  View Solution play_arrow

• question_answer15)
  The value of tan \[75{}^\circ \] is
  A)
  \[1+\frac{1}{\sqrt{3}}\] done clear
  B)
  \[2-\sqrt{3}\] done clear
  C)
  \[2+\sqrt{3}\] done clear
  D)
  \[1+\sqrt{3}\] done clear
  View Solution play_arrow

• question_answer16)
  \[\cos (A+B)cos(A-B)\] is identically equal to
  A)
  \[{{\sin }^{2}}A-{{\sin }^{2}}B\] done clear
  B)
  \[{{\cos }^{2}}A-{{\sin }^{2}}B\] done clear
  C)
  \[{{\cos }^{2}}A-{{\cos }^{2}}B\] done clear
  D)
  \[\cos 2A\,\,.\,\,\cos 2B\] done clear
  View Solution play_arrow

• question_answer17)
  \[{{\cos }^{4}}A-{{\sin }^{4}}A\] is equal to
  A)
  \[\sin 2A\] done clear
  B)
  \[-\sin 2A\] done clear
  C)
  \[\cos \,2A\] done clear
  D)
  \[-\cos \,2A\] done clear
  View Solution play_arrow

• question_answer18)
  If \[\cos \,\theta -\sin \theta =\sqrt{2}\,\sin \theta \], then \[\cos \,\theta +\sin \theta \] is
  A)
  \[\sqrt{2}\cos \,\theta \] done clear
  B)
  \[\sqrt{2}sin\,\theta \] done clear
  C)
  \[0\] done clear
  D)
  \[1\] done clear
  View Solution play_arrow

• question_answer19)
  If \[\sec \theta -\tan \theta =k\], then the value of \[\sec \theta +\tan \theta \] is
  A)
  \[(1-k)\] done clear
  B)
  \[(1+k)\] done clear
  C)
  \[\frac{1}{k}\] done clear
  D)
  \[1-\frac{1}{k}\] done clear
  View Solution play_arrow

• question_answer20)
  If \[7\sin \alpha =24\,\,\cos \alpha ;\,0<a<\frac{\pi }{2}\] , then value of 14 \[\tan \alpha -75\cos \alpha -7\sec \alpha \] is equal to
  A)
  1 done clear
  B)
  2 done clear
  C)
  3 done clear
  D)
  4 done clear
  View Solution play_arrow

• question_answer21)
  If \[\sec \beta =x+\frac{1}{4x}\] , then the value of \[\sec \beta +\tan \beta \] is
  A)
  \[2x\] done clear
  B)
  \[\frac{x}{2}\] done clear
  C)
  \[3x\] done clear
  D)
  \[\frac{x}{3}\] done clear
  View Solution play_arrow

• question_answer22)
  In an acute angled  \[\Delta ABC\], \[a=4\text{ }cm\], \[b=6\text{ }cm\], \[\sin B=\frac{3}{4}\], then the value of angle A is
  A)
  \[30{}^\circ \]   done clear
  B)
  \[45{}^\circ \] done clear
  C)
  \[60{}^\circ \] done clear
  D)
  None of these done clear
  View Solution play_arrow

• question_answer23)
  If ABC is an acute angled triangle and BD is  perpendicular to AC, then the value of \[\frac{\sin A}{\sin C}\] is
  A)
  \[\frac{AB}{BC}\] done clear
  B)
  \[\frac{BC}{AB}\] done clear
  C)
  \[\frac{BC}{CD}\] done clear
  D)
  \[\frac{CD}{BC}\] done clear
  View Solution play_arrow

• question_answer24)
  If \[A+B+C=180{}^\circ \] , then \[\tan A+\tan B+\tan C\] is equal to
  A)
  \[2\tan A\,\,\tan B\,\,\tan C\] done clear
  B)
  \[\tan A\,\,\tan B\,\,\tan C\] done clear
  C)
  \[\cot A\,\,\cot B\,\,\cot C\] done clear
  D)
  \[\tan A\,\,\tan B\,\,\cot C\] done clear
  View Solution play_arrow

• question_answer25)
  \[\tan \left( 45{}^\circ -\frac{A}{2} \right)\] is equal to
  A)
  \[\text{cosec}\,A+\cot A\] done clear
  B)
  \[\text{cosec}\,A-\cot A\] done clear
  C)
  \[\text{sec}\,A+tanA\] done clear
  D)
  \[\text{sec}\,A-tanA\] done clear
  View Solution play_arrow

• question_answer26)
  If the length of the shadow of a pole is equal to the height of the pole, then the angle of the elevation of the sun is
  A)
  \[30{}^\circ \] done clear
  B)
         \[75{}^\circ \] done clear
  C)
  \[60{}^\circ \] done clear
  D)
         \[45{}^\circ \]   done clear
  View Solution play_arrow

• question_answer27)
  The shadow of a stick of height 1 metre, when the angle of elevation of the sun is 60, will be
  A)
  \[\frac{1}{\sqrt{3}}\,\,meter\] done clear
  B)
  \[\frac{1}{3}\,\,meter\] done clear
  C)
  \[\sqrt{3}\,\,meter\] done clear
  D)
  \[3\,\,meter\] done clear
  View Solution play_arrow

• question_answer28)
  Given \[3\sin \beta +5\cos \beta =5\], then the value of \[{{(3\cos \beta -5\sin \beta )}^{2}}\] is
  A)
  \[9\] done clear
  B)
  \[\frac{9}{5}\] done clear
  C)
  \[\frac{1}{3}\] done clear
  D)
  \[\frac{1}{9}\] done clear
  View Solution play_arrow

• question_answer29)
  The value of \[{{\tan }^{2}}30{}^\circ +4{{\sin }^{2}}45{}^\circ +\frac{1}{3}{{\cos }^{2}}30{}^\circ \] is
  A)
  \[2\frac{7}{12}\] done clear
  B)
  \[1\frac{5}{12}\] done clear
  C)
  \[-2\frac{5}{12}\] done clear
  D)
  \[-1\frac{5}{12}\] done clear
  View Solution play_arrow

• question_answer30)
  The angles of the triangles ABC and DEF are given as follows : \[A=90{}^\circ ,\text{ }B=30{}^\circ ,\text{ }D=90{}^\circ \text{ }and\text{ }E=30{}^\circ \]. If the side BC is twice the side EF, then
  A)
   sin B = 2 sin E    done clear
  B)
          sin E = 2 sin B done clear
  C)
   sin B = sin E        done clear
  D)
          sin A = sin D done clear
  View Solution play_arrow

• question_answer31)
  The equation \[{{(a+b)}^{2}}=4ab\] is possible when
  A)
  \[2a=b\] done clear
  B)
  \[3a=2b\] done clear
  C)
  \[a=b\] done clear
  D)
  \[a=2b\] done clear
  View Solution play_arrow

• question_answer32)
  Two villages are 2 kms apart. If the angles of depression of these villages when observed from a plane are found to be \[45{}^\circ \] and \[60{}^\circ \] respectively, then height of the plane is
  A)
  \[(3+\sqrt{3})\,km\] done clear
  B)
  \[(3-\sqrt{3})\,km\] done clear
  C)
  \[2\sqrt{3}\,km\] done clear
  D)
  \[3\sqrt{3}\,km\] done clear
  View Solution play_arrow

• question_answer33)
  A balloon, whose radius is r, subtends an angle a at the eye of an observer, when the angle of elevation of its centre is P. The height of its centre is
  A)
  \[r\,\text{cosec}\frac{\alpha }{2}\sin \beta \] done clear
  B)
  \[\frac{r\,\text{cosec}\,\alpha }{2\sin \beta }\] done clear
  C)
  \[\frac{r\,\text{cosec}\,\alpha }{2\cos \beta }\] done clear
  D)
  \[r\sin \alpha \sin \beta \] done clear
  View Solution play_arrow

• question_answer34)
  In the given figure, the value of cosec A is
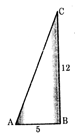
  A)
  \[\frac{5}{12}\] done clear
  B)
  \[\frac{12}{13}\] done clear
  C)
  \[\frac{5}{13}\] done clear
  D)
  \[\frac{13}{12}\] done clear
  View Solution play_arrow

• question_answer35)
  The angles of elevation of the top of a vertical tower from two points. 30 metres apart, and on the same straight line passing through the base of tower, are \[30{}^\circ \] and \[60{}^\circ \] respectively. The height of the tower is
  A)
  10 m                     done clear
  B)
  15 m done clear
  C)
  \[15\sqrt{3}\,\,m\] done clear
  D)
  30 m done clear
  View Solution play_arrow

• question_answer36)
  The greatest value of (\[\text{sin}\alpha \text{ cos}\alpha \]) is
  A)
  1             done clear
  B)
  \[\frac{1}{2}\] done clear
  C)
  \[\frac{1}{4}\] done clear
  D)
  2 done clear
  View Solution play_arrow

• question_answer37)
  For an acute angle \[\alpha ,\] \[(sin\alpha +cos\alpha )\] takes the greatest value when the value of a is equal to
  A)
  \[30{}^\circ \] done clear
  B)
  \[45{}^\circ \]   done clear
  C)
  \[60{}^\circ \] done clear
  D)
  \[90{}^\circ \] done clear
  View Solution play_arrow

• question_answer38)
  If \[\alpha +\beta =90{}^\circ \] and \[\alpha =2\beta \], then \[{{\cos }^{2}}\alpha +{{\sin }^{2}}\beta \] is
  A)
  1 done clear
  B)
  0 done clear
  C)
  \[\frac{1}{2}\] done clear
  D)
  2 done clear
  View Solution play_arrow

• question_answer39)
  Which of the following statements is not correct?
  A)
  \[{{\cos }^{4}}\theta -{{\sin }^{4}}\theta ={{\cos }^{2}}\theta -{{\sin }^{2}}\theta \] done clear
  B)
  \[1{{\tan }^{2}}\theta ={{\sec }^{2}}\theta \] done clear
  C)
  \[\sin 40{}^\circ +\cos 50{}^\circ =2\sin 40{}^\circ \] done clear
  D)
  \[{{\sin }^{2}}\theta +{{\cos }^{2}}\theta =2\] done clear
  View Solution play_arrow

• question_answer40)
  If \[\sin \theta +\cos \theta =1\], then \[(\sin \theta \cos \theta )\]is equal to
  A)
  \[0\] done clear
  B)
  \[\frac{1}{2}\] done clear
  C)
  \[1\] done clear
  D)
  \[-\frac{1}{2}\] done clear
  View Solution play_arrow

• question_answer41)
  The value of \[{{(cos\theta +sin\theta )}^{2}}+{{(cos\theta -sin\theta )}^{2}}\] is
  A)
  0 done clear
  B)
  1 done clear
  C)
  2 done clear
  D)
  3 done clear
  View Solution play_arrow

• question_answer42)
  The value of \[si{{n}^{2}}\alpha +cose{{c}^{2}}\alpha \] is always
  A)
  greater than 1 done clear
  B)
  less than 1 done clear
  C)
  greater than or equal to 2   done clear
  D)
  equal to 2 done clear
  View Solution play_arrow

• question_answer43)
  If \[\tan 30{}^\circ =x,\,\,\tan 45{}^\circ =y,\,\,\tan 60{}^\circ =z\] , then
  A)
  \[x+y=z\] done clear
  B)
  \[xy=z\] done clear
  C)
  \[xz=y\] done clear
  D)
  \[y+z=x\] done clear
  View Solution play_arrow

• question_answer44)
  The minimum value of \[{{\tan }^{2}}\alpha -{{\cot }^{2}}\alpha \] is
  A)
  2 done clear
  B)
  3 done clear
  C)
  1 done clear
  D)
  0 done clear
  View Solution play_arrow

• question_answer45)
  If \[0<\theta <\frac{\pi }{4}\,then\,(cos\theta -sin\theta )\] is
  A)
  always negative done clear
  B)
  always positive   done clear
  C)
  sometimes positive and sometimes negative done clear
  D)
  zero done clear
  View Solution play_arrow

• question_answer46)
  The value of \[1+{{\cot }^{2}}A\] is
  A)
  \[{{\cos }^{2}}A\] done clear
  B)
  \[se{{c}^{2}}A\] done clear
  C)
  \[ta{{n}^{2}}A\] done clear
  D)
  \[\text{cose}{{\text{c}}^{2}}A\] done clear
  View Solution play_arrow

• question_answer47)
  If \[\text{sin2}A=\cos A\], then the value of A is
  A)
  \[30{}^\circ \]   done clear
  B)
  \[45{}^\circ \] done clear
  C)
  \[60{}^\circ \] done clear
  D)
  \[75{}^\circ \] done clear
  View Solution play_arrow

• question_answer48)
  If \[A+B=\frac{\pi }{2}\], then value of \[\sin A\cos B+\cos A\sin B\] is
  A)
  \[0\] done clear
  B)
  \[1\] done clear
  C)
  \[\frac{1}{2}\] done clear
  D)
  \[\frac{\sqrt{3}}{2}\] done clear
  View Solution play_arrow

• question_answer49)
  The value of \[4{{\cot }^{2}}\frac{\pi }{3}+{{\sec }^{2}}\frac{\pi }{6}-{{\sin }^{2}}\frac{\pi }{4}\] is
  A)
  \[\frac{13}{6}\] done clear
  B)
  \[\frac{1}1{6}\] done clear
  C)
  \[\frac{7}{6}\] done clear
  D)
  \[\frac{5}{6}\] done clear
  View Solution play_arrow

• question_answer50)
  The value of \[{{\cos }^{2}}30{}^\circ -{{\cos }^{2}}60{}^\circ -\cos 60{}^\circ \] is
  A)
  0 done clear
  B)
  \[\frac{1}{2}\] done clear
  C)
  \[\frac{3}{4}\] done clear
  D)
  1 done clear
  View Solution play_arrow

• question_answer51)
  The value  of \[\frac{{{\tan }^{2}}60{}^\circ -2{{\tan }^{2}}45{}^\circ +se{{c}^{2}}30{}^\circ }{3si{{n}^{2}}45{}^\circ \sin 90{}^\circ +co{{s}^{2}}60{}^\circ co{{s}^{3}}0{}^\circ }\]
  A)
  \[\frac{49}{12}\] done clear
  B)
  \[\frac{7}{3}\] done clear
  C)
  \[\frac{14}{9}\] done clear
  D)
  \[\frac{4}{3}\] done clear
  View Solution play_arrow

• question_answer52)
  If \[\sin \theta =\frac{8}{17}\] where \[0{}^\circ <\theta <90{}^\circ \], then \[\tan \theta +\sec \theta \] is
  A)
  \[\frac{1}{3}\] done clear
  B)
  \[\frac{2}{3}\] done clear
  C)
  \[\frac{4}{3}\] done clear
  D)
  \[\frac{5}{3}\] done clear
  View Solution play_arrow

• question_answer53)
  Which one of the following is correct?
  A)
  \[\sin 45{}^\circ \cos 45{}^\circ =1\] done clear
  B)
  \[{{\sin }^{2}}45{}^\circ -{{\cos }^{2}}45{}^\circ =1\] done clear
  C)
  \[\sin 30{}^\circ +\cos 60{}^\circ =1\] done clear
  D)
  \[co{{s}^{2}}30{}^\circ -\cos 60{}^\circ =1\] done clear
  View Solution play_arrow

• question_answer54)
  \[\frac{\tan \theta }{{{(1+{{\tan }^{2}}\theta )}^{2}}}+\frac{cot\theta }{{{(1+{{\cot }^{2}}\theta )}^{2}}}\] is equal to
  A)
  \[2\sin \theta \,\,.\,\,\cos \theta \] done clear
  B)
  \[\operatorname{cosec}\theta \,\,.\,\,sec\theta \] done clear
  C)
  \[\sin \,\theta \,\,.\,\,cos\theta \] done clear
  D)
  \[2cosec\,\theta \,\,.\,\,sin\theta \] done clear
  View Solution play_arrow

• question_answer55)
  Equation \[6{{\sin }^{2}}\theta -5\sin \theta +1=0\] is satisfied h
  A)
  \[\theta =\frac{\pi }{2}\] done clear
  B)
  \[\theta =\frac{\pi }{3}\] done clear
  C)
  \[\theta =\frac{\pi }{4}\] done clear
  D)
  \[\theta =\frac{\pi }{6}\] done clear
  View Solution play_arrow

• question_answer56)
  If \[\theta \] increases from \[0{}^\circ \] to \[90{}^\circ \], then the value of \[\cos \theta \]
  A)
   decreases   done clear
  B)
   increases done clear
  C)
   neither increases or decreases done clear
  D)
   none of these done clear
  View Solution play_arrow

• question_answer57)
  The value of \[4(si{{n}^{4}}30{}^\circ +co{{s}^{4}}60{}^\circ )(co{{s}^{2}}45{}^\circ -si{{n}^{2}}90{}^\circ )+ta{{n}^{4}}45{}^\circ -{{\cot }^{2}}45{}^\circ \] is
  A)
  \[0\] done clear
  B)
  \[1\] done clear
  C)
  \[-\frac{1}{4}\] done clear
  D)
  \[-2\] done clear
  View Solution play_arrow

• question_answer58)
  If \[\tan \theta =4\], then \[\left( \frac{\tan \theta }{\frac{{{\sin }^{3}}\theta }{\cos \theta }+\sin \theta \cos \theta } \right)\] is equal to
  A)
  \[0\] done clear
  B)
  \[2\sqrt{2}\] done clear
  C)
  \[\sqrt{2}\] done clear
  D)
  \[1\] done clear
  View Solution play_arrow

• question_answer59)
  In a AABC, AD is perpendicular to BC, then \[\frac{AC}{AB}\] is equal to
  A)
  \[\frac{\sin C}{\sin B}\] done clear
  B)
  \[\frac{\cos B}{\cos C}\] done clear
  C)
  \[\frac{\sin B}{\sin C}\] done clear
  D)
  \[\frac{tanB}{tanC}\] done clear
  View Solution play_arrow

• question_answer60)
  \[\frac{\tan \theta }{\sec \theta -1}+\frac{\tan \theta }{\sec \theta +1}\] is equal to
  A)
  \[\operatorname{cosec}\,\theta \] done clear
  B)
  \[2\operatorname{cosec}\,\theta \] done clear
  C)
  \[sec\,\theta \] done clear
  D)
  \[2sec\,\theta \] done clear
  View Solution play_arrow

• question_answer61)
  The expression \[{{(tan\theta +\sec \theta )}^{2}}\] is equal to
  A)
  \[\frac{1+\cos \theta }{1-\cos \theta }\] done clear
  B)
  \[\frac{1+sin\theta }{1-sin\theta }\] done clear
  C)
  \[\frac{1-\cos \theta }{1+\cos \theta }\] done clear
  D)
  \[\frac{1-sin\theta }{1+sin\theta }\] done clear
  View Solution play_arrow

• question_answer62)
  \[{{\sec }^{2}}\theta +{{\operatorname{cosec}}^{2}}\theta \] is equal to
  A)
  \[{{\sec }^{2}}\theta \,\,.\,\,\,{{\cot }^{2}}\theta \] done clear
  B)
  \[{{\sec }^{2}}\theta \,\,.\,\,\,ta{{n}^{2}}\theta \] done clear
  C)
  \[cose{{c}^{2}}\theta \,\,.\,\,\,{{\cot }^{2}}\theta \] done clear
  D)
  \[se{{c}^{2}}\theta \,\,.\,\,\,{{\operatorname{cosec}}^{2}}\theta \] done clear
  View Solution play_arrow

• question_answer63)
  The expression \[3{{(\sin x-\cos x)}^{4}}+6{{(sinx+\cos x)}^{2}}+4(si{{n}^{6}}x+{{\cos }^{6}}x)\] is equal to
  A)
  10 done clear
  B)
  11 done clear
  C)
  12 done clear
  D)
  13 done clear
  View Solution play_arrow

• question_answer64)
  If \[n=\frac{\cos \alpha }{\cos \beta },\,\,m=\frac{sin\alpha }{sin\beta }\] then \[({{m}^{2}}-{{n}^{2}}){{\sin }^{2}}\beta \] is
  A)
  \[1-n\] done clear
  B)
  \[1+n\] done clear
  C)
  \[1-{{n}^{2}}\] done clear
  D)
  \[1+{{n}^{2}}\] done clear
  View Solution play_arrow

• question_answer65)
  The value of \[\sqrt{3}\,\,\operatorname{cosec}\,\,20{}^\circ -\sec \,\,20{}^\circ \] is
  A)
  4.5                         done clear
  B)
  4   done clear
  C)
  8                             done clear
  D)
  9 done clear
  View Solution play_arrow

• question_answer66)
  The value of \[\tan 5{}^\circ \,\tan 10{}^\circ \tan 15{}^\circ \tan 20{}^\circ .....\tan 85{}^\circ \], is
  A)
  1 done clear
  B)
  2 done clear
  C)
  3 done clear
  D)
  None of these done clear
  View Solution play_arrow

• question_answer67)
  In a right angled triangle \[ABC,\] right angled at \[C,\] the value of \[\sin A\cos B+\cos A\sin B\] is
  A)
  5 done clear
  B)
  1 done clear
  C)
  2 done clear
  D)
  3 done clear
  View Solution play_arrow

• question_answer68)
  If \[\sin \theta +\cos \theta =2,\,\,0{}^\circ \le \theta \le 90{}^\circ \] ,then \[\sin \theta -2\cos \theta \] is
  A)
  0 done clear
  B)
  -1 done clear
  C)
  1 done clear
  D)
  2 done clear
  View Solution play_arrow

• question_answer69)
  If \[\sec \theta -\tan \theta =p\] , then the value of \[\sin \theta \] is
  A)
  \[\frac{1-{{p}^{2}}}{2(1+{{p}^{2}})}\] done clear
  B)
  \[\frac{1+{{p}^{2}}}{2(1-{{p}^{2}})}\] done clear
  C)
  \[\frac{1-2p}{1+{{p}^{2}}}\] done clear
  D)
  \[\frac{1-{{p}^{2}}}{1+{{p}^{2}}}\] done clear
  View Solution play_arrow

• question_answer70)
  If \[x=a\,\sin \theta ,\,\,y=b\,\tan \theta \], then
  A)
  \[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\] done clear
  B)
  \[\frac{{{a}^{2}}}{{{x}^{2}}}+\frac{{{b}^{2}}}{{{y}^{2}}}=1\] done clear
  C)
  \[\frac{{{a}^{2}}}{{{x}^{2}}}-\frac{{{b}^{2}}}{{{y}^{2}}}=1\] done clear
  D)
  \[\frac{{{x}^{2}}}{{{a}^{2}}}-\frac{{{y}^{2}}}{{{b}^{2}}}=1\] done clear
  View Solution play_arrow

• question_answer71)
  The value of \[\frac{\cos \theta }{\sin (90{}^\circ +\theta )}+\frac{sin\theta }{\sin (180{}^\circ +\theta )}+\frac{\cot (90{}^\circ -\theta )}{\tan \theta }\]
  A)
  1 done clear
  B)
  2 done clear
  C)
  3 done clear
  D)
  4 done clear
  View Solution play_arrow

• question_answer72)
  If \[\sin x+\sin 2x-\sin 3x=3\], then the value of \[x\] is
  A)
  \[30{}^\circ \] done clear
  B)
  \[45{}^\circ \] done clear
  C)
  \[60{}^\circ \] done clear
  D)
  None of these   done clear
  View Solution play_arrow

• question_answer73)
  The value of \[\sin \theta \,\,.\,\,\cos \theta \] has maximum value when \[\theta \] is
  A)
  \[30{}^\circ \] done clear
  B)
  \[45{}^\circ \]   done clear
  C)
  \[60{}^\circ \] done clear
  D)
  \[90{}^\circ \] done clear
  View Solution play_arrow

• question_answer74)
  If \[\sin 50=0.766,\] then value of sec \[40{}^\circ \] is
  A)
  1 done clear
  B)
  .766 done clear
  C)
  \[\frac{1}{766}\]                 done clear
  D)
  0 done clear
  View Solution play_arrow

• question_answer75)
  The value of \[\tan \theta \,.\,\,tan(90-\theta )\] is equal to
  A)
  \[{{\sin }^{2}}\theta \] done clear
  B)
  \[1\] done clear
  C)
  \[{{\cos }^{2}}\theta \] done clear
  D)
  \[0\] done clear
  View Solution play_arrow

• question_answer76)
  The value of \[\frac{{{\sin }^{2}}A}{1-\cos 2A}\] is
  A)
  \[\frac{1}{2}\] done clear
  B)
  \[0\] done clear
  C)
  \[1\] done clear
  D)
  \[\sqrt{3}\] done clear
  View Solution play_arrow

• question_answer77)
  The minimum value of \[\sin \theta \,\,\cos \theta \] is
  A)
  \[0\] done clear
  B)
  \[-1\] done clear
  C)
  \[-\frac{1}{2}\] done clear
  D)
  \[\frac{1}{2}\] done clear
  View Solution play_arrow

• question_answer78)
  Which of the following identities is true?
  A)
  \[\sin 2x[\tan x+\cot x]=2\] done clear
  B)
  \[1-cos2x=2co{{s}^{2}}x\] done clear
  C)
  \[ta{{n}^{2}}x+{{\cot }^{2}}x={{\sec }^{2}}x+{{\operatorname{cosec}}^{2}}x\] done clear
  D)
  \[{{\cot }^{2}}x-{{\tan }^{2}}x=1\] done clear
  View Solution play_arrow

• question_answer79)
  If \[\cos \theta =\frac{3}{5}\] , then the value of \[\frac{\sin \theta \,.\,\,\tan \theta +1}{2{{\tan }^{2}}\theta }\]
  A)
  \[\frac{88}{160}\] done clear
  B)
    \[\frac{91}{160}\] done clear
  C)
    \[\frac{92}{160}\] done clear
  D)
    \[\frac{93}{160}\] done clear
  View Solution play_arrow

• question_answer80)
  The value of \[\frac{1}{\sin 10{}^\circ }-\frac{\sqrt{3}}{\cos 10{}^\circ }\] is
  A)
  2 done clear
  B)
  1 done clear
  C)
  4 done clear
  D)
  3 done clear
  View Solution play_arrow

• question_answer81)
  The value of \[\frac{\cot \theta +\operatorname{cosec}\theta -1}{\cot \theta -\operatorname{cosec}\theta +1}\] is
  A)
  \[\frac{1+\cos \theta }{\sin \theta }\] done clear
  B)
  \[\frac{1+\sin \theta }{\sin \theta }\] done clear
  C)
  \[\frac{1-\cos \theta }{\sin \theta }\] done clear
  D)
  \[\frac{1-sin\theta }{\sin \theta }\] done clear
  View Solution play_arrow

• question_answer82)
  If \[\cos (A-B)=sin(A+B)=\frac{1}{2},\] where A and B are positive, then smallest positive value of A + B (in degrees) is
  A)
  \[45{}^\circ \] done clear
  B)
  \[60{}^\circ \] done clear
  C)
  \[105{}^\circ \] done clear
  D)
  \[150{}^\circ \]   done clear
  View Solution play_arrow

• question_answer83)
  From the top of a house 32 meters high, if the angle of elevation of the top of a tower is \[45{}^\circ \] and the angle of depression of the foot of the tower is \[30{}^\circ \], then the height of the tower is
  A)
  \[\frac{32}{\sqrt{3}}(\sqrt{3}+1)\,\,meters\] done clear
  B)
  \[32(\sqrt{3}+1)\,\,meters\] done clear
  C)
  \[32\sqrt{3}\,\,meters\] done clear
  D)
  \[\frac{32}{3}(\sqrt{3}+1)\,\,meters\] done clear
  View Solution play_arrow

• question_answer84)
  If the angle of elevation of an object from a point 200 meters above the lake is found to be \[30{}^\circ \] and the angle of depression of its image in the lake is \[45{}^\circ \], then the height of the object above the lake is
  A)
  \[\frac{200(\sqrt{3}-1)}{(\sqrt{3}+1)}\,\,meters\] done clear
  B)
  \[\frac{200(\sqrt{3}-1)}{\sqrt{3}}\,\,meters\] done clear
  C)
  \[\frac{200(\sqrt{3}+1)}{\sqrt{3}}\,\,meters\] done clear
  D)
    \[\frac{200(\sqrt{3}+1)}{(\sqrt{3}-1)}\,\,meters\]   done clear
  View Solution play_arrow

• question_answer85)
  The angle of elevation of the top of a tower at distance of 500 meters from the foot is \[30{}^\circ \] The height of the tower is
  A)
  \[250\sqrt{3}\,\,meters\] done clear
  B)
  \[\frac{500}{\sqrt{3}}\,\,meters\] done clear
  C)
  \[500\sqrt{3}\,\,meters\] done clear
  D)
  \[250\,\,meters\] done clear
  View Solution play_arrow

• question_answer86)
  The angles of elevation of the top of a tower from two points distant a and b (a > b) from its foot and in the same straight line from it are \[30{}^\circ \] and \[60{}^\circ \]. The height of the tower is
  A)
  \[\frac{a}{b}\] done clear
  B)
  \[\sqrt{\frac{a}{b}}\] done clear
  C)
  \[ab\] done clear
  D)
  \[\sqrt{ab}\] done clear
  View Solution play_arrow

• question_answer87)
  The value-of sin \[105{}^\circ \] is
  A)
  \[\frac{\sqrt{3}-1}{2\sqrt{2}}\] done clear
  B)
  \[\frac{\sqrt{3}-1}{\sqrt{2}}\] done clear
  C)
  \[\frac{\sqrt{3}+1}{2\sqrt{2}}\] done clear
  D)
  \[\frac{\sqrt{3}+1}{\sqrt{2}}\] done clear
  View Solution play_arrow

• question_answer88)
  If \[\tan \theta =\sqrt{2}\], then the value of \[\theta \] is
  A)
  \[less\text{ }than\,\,\frac{\pi }{4}\] done clear
  B)
  \[equal\text{ }to\,\,\frac{\pi }{4}\] done clear
  C)
  \[between\,\,\frac{\pi }{4}\,\,and\,\,\frac{\pi }{3}\] done clear
  D)
  \[greater\text{ }than\,\,\frac{\pi }{3}\] done clear
  View Solution play_arrow

• question_answer89)
  If \[\tan \theta =2-\sqrt{3}\], then \[\tan (90{}^\circ -\theta )\] is equal to
  A)
  \[2+\sqrt{3}\] done clear
  B)
  \[2-\sqrt{3}\] done clear
  C)
  \[3+\sqrt{3}\] done clear
  D)
  \[3-\sqrt{3}\] done clear
  View Solution play_arrow

• question_answer90)
  If the angles of depression and elevation of the top of a tower of height h from the top and bottom of a second tower are x and y respectively, then height of the second tower is
  A)
  \[h(\cot \,y+\cot \,x)\] done clear
  B)
  \[h(tan\,x+tan\,y)\] done clear
  C)
  \[h(1+tan\,x\cot \,y)\] done clear
  D)
  \[h(tan\,y\cot \,x+1)\] done clear
  View Solution play_arrow

• question_answer91)
  A man on the top of a bamboo pole observes that the angles of depression of the base and the top of another pole are \[60{}^\circ \] and \[30{}^\circ \] respectively. If the second pole stands 5 m above the ground level, then the height of the bamboo, on which the man is sitting, is
  A)
   5 m                        done clear
  B)
          7.5 m   done clear
  C)
   10 m                     done clear
  D)
          12.5 m done clear
  View Solution play_arrow

• question_answer92)
  The value of sin \[105{}^\circ \]. sin \[75{}^\circ \] is
  A)
  \[\frac{\sqrt{3}+2}{4}\] done clear
  B)
  \[\frac{\sqrt{3}+2}{2}\] done clear
  C)
  \[\frac{\sqrt{3}-2}{4}\] done clear
  D)
  \[\frac{\sqrt{3}-2}{2}\] done clear
  View Solution play_arrow

• question_answer93)
  If \[\frac{1}{4}\] is in the first quadrant and \[\cos \theta =\frac{3}{5}\], then value of \[\frac{5tan\theta -4\operatorname{cosec}\theta }{5\sec \theta -4\cot \theta }\] is
  A)
  \[\frac{5}{34}\] done clear
  B)
  \[\frac{5}{16}\] done clear
  C)
  \[\frac{5}{-34}\] done clear
  D)
  \[\frac{-5}{16}\] done clear
  View Solution play_arrow

• question_answer94)
  It \[2si{{n}^{2}}\theta +{{\cos }^{2}}45{}^\circ =\tan 45{}^\circ \] and \[0\le \theta \le 90{}^\circ \], then the value of \[\tan \theta \] is
  A)
  \[\sqrt{3}\] done clear
  B)
  \[1\] done clear
  C)
  \[\frac{1}{\sqrt{3}}\] done clear
  D)
  not defined done clear
  View Solution play_arrow

• question_answer95)
  The value of \[{{\cos }^{2}}\left( \frac{\pi }{4} \right)+{{\cos }^{4}}\left( \frac{\pi }{6} \right)+si{{n}^{4}}\left( \frac{\pi }{6} \right)+si{{n}^{4}}\left( \frac{\pi }{3} \right)\] is
  A)
  \[\frac{27}{16}\] done clear
  B)
  \[\frac{7}{16}\] done clear
  C)
  \[\frac{5}{16}\] done clear
  D)
  \[\frac{3}{16}\] done clear
  View Solution play_arrow

• question_answer96)
  Which one of the following statements is true?
  A)
  \[\cos (A+B)=cosA+\operatorname{cosB}\] done clear
  B)
  \[\cos (A+B)=cosA\operatorname{cosB}\] done clear
  C)
  \[\cos (A+B)=cosA\operatorname{cosB}-\sin A\sin B\] done clear
  D)
  \[\cos (A+B)=cosA\operatorname{cosB}+\sin A\sin B\] done clear
  View Solution play_arrow

• question_answer97)
  From the point B a perpendicular BD is drawn on AC. If \[\cos 30=0.8\], find the length of AD.  
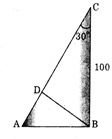
  A)
  45 done clear
  B)
  30 done clear
  C)
  50 done clear
  D)
  80 done clear
  View Solution play_arrow

• question_answer98)
  The value of \[32{{\cot }^{2}}\frac{\pi }{4}-8{{\sec }^{2}}\frac{\pi }{3}+8co{{s}^{3}}\frac{\pi }{6}\] is
  A)
  \[3\sqrt{3}\] done clear
  B)
  \[2\sqrt{3}\] done clear
  C)
  \[\sqrt{3}\] done clear
  D)
  \[6\sqrt{3}\] done clear
  View Solution play_arrow

• question_answer99)
  Given that \[\cos 50{}^\circ \,\,18'=0.6388\] and \[\cos 50{}^\circ \,42'=0.6334\], then the possible value of \[\cos 50{}^\circ \,20'\] is
  A)
  0.6293            done clear
  B)
  0.6307 done clear
  C)
  0.6361     done clear
  D)
  0.6414 done clear
  View Solution play_arrow

• question_answer100)
  In \[\Delta ABC\], angle C is a right angle, then the value of \[\tan A+\tan B\] is
  A)
  \[\tan \,C\] done clear
  B)
  \[c\] done clear
  C)
  \[\frac{c}{ab}\] done clear
  D)
  \[\frac{{{c}^{2}}}{ab}\] done clear
  View Solution play_arrow

• question_answer101)
  Which one of the following relations is true?
  A)
  \[{{\cos }^{2}}\theta -{{\sin }^{2}}\theta =1\] done clear
  B)
  \[{{\operatorname{cosec}}^{2}}\theta -{{\sec }^{2}}\theta =1\] done clear
  C)
  \[{{\cot }^{2}}\theta -{{\tan }^{2}}\theta =1\] done clear
  D)
  \[se{{c}^{2}}\theta -{{\tan }^{2}}\theta =1\] done clear
  View Solution play_arrow

• question_answer102)
  If \[\alpha \cos \theta +b\,\sin \theta =m\] and \[\alpha sin\theta -b\,\cos \theta =n\], then the value of \[{{a}^{2}}+{{b}^{2}}\] is
  A)
  \[m+n\] done clear
  B)
  \[m\,n\] done clear
  C)
  \[\sqrt{m\,n}\] done clear
  D)
  \[{{m}^{2}}+{{n}^{2}}\] done clear
  View Solution play_arrow

• question_answer103)
  If \[\theta \] is any angle, then \[{{\sec }^{2}}\theta -{{\sec }^{2}}\theta \] is equals to
  A)
  \[ta{{n}^{4}}\theta -{{\tan }^{2}}\theta \] done clear
  B)
  \[ta{{n}^{2}}\theta -{{\tan }^{4}}\theta \] done clear
  C)
  \[ta{{n}^{2}}\theta +{{\tan }^{4}}\theta \] done clear
  D)
  \[2ta{{n}^{2}}\theta \] done clear
  View Solution play_arrow

• question_answer104)
  The value of \[{{\sin }^{2}}60{}^\circ +\tan 45{}^\circ -{{\operatorname{cosec}}^{2}}45{}^\circ \] is
  A)
  \[-\frac{1}{2}\] done clear
  B)
  \[-\frac{1}{4}\] done clear
  C)
  \[\frac{1}{4}\] done clear
  D)
  \[\frac{1}{2}\] done clear
  View Solution play_arrow

• question_answer105)
  If \[\sin \theta +\cos \theta =\sqrt{2}\] and \[\theta \] is acute, then \[\tan \theta \] is equal to
  A)
  \[\frac{1}{\sqrt{3}}\] done clear
  B)
  \[1\] done clear
  C)
  \[\sqrt{3}\] done clear
  D)
  \[\infty \] done clear
  View Solution play_arrow

• question_answer106)
  The value of \[{{\cos }^{4}}\frac{\pi }{4}-{{\cos }^{4}}\frac{\pi }{6}+si{{n}^{4}}\frac{\pi }{6}+si{{n}^{4}}\frac{\pi }{3}\] is
  A)
  \[\frac{1}{16}\] done clear
  B)
  \[\frac{1}{8}\] done clear
  C)
  \[\frac{5}{16}\] done clear
  D)
  \[\frac{3}{16}\] done clear
  View Solution play_arrow

• question_answer107)
  If \[\tan \theta =\frac{3}{4}\] and \[0<9,\,<90{}^\circ \], then the value of \[\sin \theta \cos \theta \]
  A)
  \[\frac{1}{5}\] done clear
  B)
  \[\frac{9}{5}\] done clear
  C)
  \[\frac{12}{25}\] done clear
  D)
  \[\frac{25}{12}\] done clear
  View Solution play_arrow

• question_answer108)
  \[\tan \theta (1-co{{t}^{2}}\theta )\] is equal to
  A)
  \[\cot \theta (1-ta{{n}^{2}}\theta )\] done clear
  B)
  \[\cot \theta (ta{{n}^{2}}\theta -1)\] done clear
  C)
  \[\cot \theta ta{{n}^{2}}\theta \] done clear
  D)
  \[tan\theta {{\operatorname{cosec}}^{2}}\theta \] done clear
  View Solution play_arrow

• question_answer109)
  \[{{\sin }^{6}}\theta +{{\sin }^{4}}\theta \,\,.\,\,{{\cos }^{2}}\theta -si{{n}^{2}}\theta \,\,.\,\,{{\cos }^{4}}\theta -{{\cos }^{6}}\theta \] is equal to
  A)
  \[si{{n}^{2}}\theta +{{\cos }^{2}}\theta \] done clear
  B)
  \[si{{n}^{3}}\theta -{{\cos }^{3}}\theta \] done clear
  C)
  \[si{{n}^{4}}\theta +{{\cos }^{4}}\theta \] done clear
  D)
  \[si{{n}^{2}}\theta -{{\cos }^{2}}\theta \] done clear
  View Solution play_arrow

• question_answer110)
  \[{{\left[ \frac{1+\tan \theta }{1+\cot \theta } \right]}^{4}}\] is equal to
  A)
  \[{{\left( \frac{1+{{\tan }^{2}}\theta }{1+{{\cot }^{2}}\theta } \right)}^{2}}\] done clear
  B)
  \[{{\left( \frac{1+{{\cot }^{2}}\theta }{1+ta{{n}^{2}}\theta } \right)}^{2}}\] done clear
  C)
  \[{{\left( \frac{1+\tan \theta }{1-\cot \theta } \right)}^{2}}\] done clear
  D)
  \[{{\left( \frac{1-{{\cot }^{2}}\theta }{1+ta{{n}^{2}}\theta } \right)}^{2}}\] done clear
  View Solution play_arrow

• question_answer111)
  \[\frac{{{\tan }^{2}}\theta }{{{(1+sec\theta )}^{2}}}\] is equal to
  A)
  \[\left( \frac{1-cos\theta }{1+\cos \theta } \right)\] done clear
  B)
  \[\left( \frac{1+cos\theta }{1-\cos \theta } \right)\] done clear
  C)
  \[\left( \frac{cos\theta -1}{\cos \theta +1} \right)\] done clear
  D)
  \[\left( \frac{cos\theta +1}{\cos \theta -1} \right)\] done clear
  View Solution play_arrow

• question_answer112)
  For all values of \[\theta ,\cos \theta \,.\,\,cosec\theta \sqrt{{{\sec }^{2}}\theta -1}\] is
  A)
  \[1\] done clear
  B)
  \[{{\cos }^{2}}\theta \] done clear
  C)
  \[\cot \theta \] done clear
  D)
  \[tan\theta \] done clear
  View Solution play_arrow

• question_answer113)
  Which is true for all values of \[\theta \] ?
  A)
  \[{{\sin }^{2}}\theta -{{\cos }^{2}}\theta =1\] done clear
  B)
  \[cose{{c}^{2}}\theta -{{\cot }^{2}}\theta =1\] done clear
  C)
  \[cose{{c}^{2}}\theta -{{\cos }^{2}}\theta =1\] done clear
  D)
    \[se{{c}^{2}}\theta -si{{n}^{2}}\theta =1\]   done clear
  View Solution play_arrow

• question_answer114)
    As \[x\] increases from \[0\,\,to\,\,\frac{\pi }{2}\], the value of \[\cos x\]  
  A)
   increases done clear
  B)
  decreases   done clear
  C)
  remains constant done clear
  D)
  increases, then decreases done clear
  View Solution play_arrow

• question_answer115)
  Which one of the following is false?            
  A)
  \[\sin \theta =1-\cos \theta \] done clear
  B)
  \[sec\theta -\tan \theta =\frac{1}{\sec \theta +\tan \theta }\] done clear
  C)
  \[{{\tan }^{2}}\theta -{{\sin }^{2}}\theta ={{\tan }^{2}}\theta {{\sin }^{2}}\theta \] done clear
  D)
  \[\sin \frac{\pi }{3}=\cos \frac{\pi }{6}\] done clear
  View Solution play_arrow

• question_answer116)
  \[\frac{3-4{{\sin }^{2}}\theta }{{{\cos }^{2}}\theta }\] is equal to
  A)
  \[3-{{\cot }^{2}}\theta \] done clear
  B)
  \[3+{{\cot }^{2}}\theta \] done clear
  C)
  \[3-ta{{n}^{2}}\theta \] done clear
  D)
  \[3+ta{{n}^{2}}\theta \] done clear
  View Solution play_arrow

• question_answer117)
    \[(1-si{{n}^{2}}\theta )(1+ta{{n}^{2}}\theta )\] is equal to  
  A)
  1 done clear
  B)
  1.5 done clear
  C)
  2 done clear
  D)
  2.5 done clear
  View Solution play_arrow

• question_answer118)
  \[(cosec\theta -sin\theta )(sec\theta -\cos \theta )(tan\theta +\cot \theta )\] simplifies to
  A)
  \[0\] done clear
  B)
  \[1\] done clear
  C)
  \[\tan \theta \] done clear
  D)
  \[cot\theta \] done clear
  View Solution play_arrow

• question_answer119)
  Upper part of a vertical tree which is broken over by the winds just touches the ground and makes an angle of \[30{}^\circ \] with the ground. If the length of the broken part is 20 metres, then the remaining part of the tree is of length
  A)
  \[20\text{ }meters\] done clear
  B)
  \[10\sqrt{3}\text{ }meters\] done clear
  C)
  \[10\text{ }meters\] done clear
  D)
  \[10\sqrt{2}\text{ }meters\] done clear
  View Solution play_arrow

• question_answer120)
  The angle of elevation of a tower from a point on the ground is \[30{}^\circ \]. At a point on the horizontal line passing through the foot of the tower and 100 metres nearer to it. If the angle of elevation is found to be \[60{}^\circ \], then height of the tower is
  A)
  \[50\sqrt{3}\text{ }meters\] done clear
  B)
  \[\frac{50}{\sqrt{3}}\text{ }meters\] done clear
  C)
  \[100\sqrt{3}\text{ }meters\] done clear
  D)
    \[\frac{100}{\sqrt{3}}\text{ }meters\]   done clear
  View Solution play_arrow

• question_answer121)
  The angles of depression of two boats as observed from the mast head of a ship 50 metres high are \[45{}^\circ \] and \[30{}^\circ \]. The distance between the boats, if they are on the same side of mast head in line with it, is
  A)
  \[50\sqrt{3}\,\,m\] done clear
  B)
  \[50(\sqrt{3}+1)\,\,m\] done clear
  C)
  \[50(\sqrt{3}-1)\,\,m\] done clear
  D)
  \[5\left( 1-\frac{1}{\sqrt{3}} \right)\,\,m\] done clear
  View Solution play_arrow

• question_answer122)
  The angle of elevation of a tower from m a point is  \[30{}^\circ \]. At a point on the horizontal line passing through the foot of the tower and 50 metres nearer it, the angle of elevation is \[60{}^\circ \]. The distance of the first point from the tower is
  A)
   50 metres        done clear
  B)
          75 metres   done clear
  C)
   100 metres        done clear
  D)
          150 metres done clear
  View Solution play_arrow

• question_answer123)
  The angle of elevation of the top of a tower as observed from a point on the horizontal ground is x. If we move a distance d towards the foot of the tower, the angle of elevation increases to y, then the height of the tower is
  A)
  \[\frac{d\tan x\tan y}{\tan y-\tan x}\] done clear
  B)
  \[d(\tan y+\tan x)\] done clear
  C)
  \[d(\tan y-\tan x)\] done clear
  D)
  \[\frac{d\tan x\tan y}{\tan y+\tan x}\] done clear
  View Solution play_arrow

• question_answer124)
  The angle of elevation of a cloud from a point h metres above the surface of a lake is \[30{}^\circ \] and the angle of depression of its reflection is \[60{}^\circ \]. Then the height of the cloud above the surface of the lake is
  A)
  \[\frac{h}{\sqrt{3}}\] done clear
  B)
  \[h\] done clear
  C)
  \[\sqrt{2}h\] done clear
  D)
  \[2h\] done clear
  View Solution play_arrow

• question_answer125)
    For an acute angle \[\alpha ,\,\sin \alpha +\cos \alpha \] takes the greatest value when \[\alpha \] is  
  A)
  \[30{}^\circ \] done clear
  B)
  \[45{}^\circ \]   done clear
  C)
  \[60{}^\circ \] done clear
  D)
  \[90{}^\circ \] done clear
  View Solution play_arrow

• question_answer126)
  If \[\beta \] is acute and \[\sin \beta =\frac{4}{5}\] the value of \[\frac{1-\frac{\sin \beta }{\tan \beta }}{1+\frac{\sin \beta }{\tan \beta }}\]
  A)
  \[\frac{1}{4}\] done clear
  B)
  \[\frac{3}{4}\] done clear
  C)
  \[\frac{3}{5}\] done clear
  D)
  \[\frac{5}{3}\] done clear
  View Solution play_arrow

• question_answer127)
  If \[\tan \theta =\frac{1}{\sqrt{5}}\] and \[\theta \] lies in the first quadrant then the value of \[\cos \theta \] is
  A)
  \[\frac{1}{\sqrt{6}}\] done clear
  B)
  \[-\frac{1}{\sqrt{6}}\] done clear
  C)
  \[-\sqrt{\frac{5}{6}}\] done clear
  D)
  \[\frac{\sqrt{5}}{\sqrt{6}}\] done clear
  View Solution play_arrow

• question_answer128)
  If the angle \[\alpha \] lies in the first quadrant and \[\tan \alpha +cot\alpha =2\], then the value of \[\sqrt{\tan \alpha }+\sqrt{cot\alpha }\]
  A)
  -4 done clear
  B)
  -2 done clear
  C)
  2 done clear
  D)
  4 done clear
  View Solution play_arrow

• question_answer129)
  If \[\tan A-\tan B=x\] and \[\cot B-\cot A=y\], then the value of \[\cot (A-B)\] is
  A)
  \[x-y\] done clear
  B)
  \[x+y\] done clear
  C)
  \[\frac{1}{x}-\frac{1}{y}\] done clear
  D)
  \[\frac{1}{x}+\frac{1}{y}\] done clear
  View Solution play_arrow

• question_answer130)
  Which one of the following is not correct?
  A)
  \[\frac{(sinA+sinB)}{(sinA-sinB)}=\frac{\tan \frac{A+B}{2}}{\tan \frac{A-B}{2}}\] done clear
  B)
  \[{{\sin }^{2}}A-{{\cos }^{2}}B=\sin (A+B)sin(A-B)\] done clear
  C)
  \[cosA-\cos B=2\cos \frac{A+B}{2}coss\frac{B-A}{2}\] done clear
  D)
    \[co{{s}^{2}}A-{{\cos }^{2}}B=\sin (A+B)sin(B-A)\]   done clear
  View Solution play_arrow

• question_answer131)
  The expression \[{{\cos }^{4}}\theta -{{\sin }^{4}}\theta +2{{\sin }^{2}}\theta \] has the value
  A)
  \[0\] done clear
  B)
  \[{{\sin }^{2}}\theta \] done clear
  C)
  \[co{{s}^{2}}\theta \] done clear
  D)
  \[1\] done clear
  View Solution play_arrow

• question_answer132)
  In\[\Delta ABC,\,\,a=4\,cm,\,\,b=6\,cm\] and \[\angle C=30{}^\circ \], then the area of the triangle is
  A)
  \[12\,\,c{{m}^{2}}\] done clear
  B)
  \[6\sqrt{2}\,c{{m}^{2}}\] done clear
  C)
  \[\frac{12}{\sqrt{3}}\,c{{m}^{2}}\] done clear
  D)
  \[6\,\,c{{m}^{2}}\] done clear
  View Solution play_arrow

• question_answer133)
  The value of \[\tan 225{}^\circ +\cot 135{}^\circ \] is
  A)
  -2 done clear
  B)
  -1 done clear
  C)
  0 done clear
  D)
  1 done clear
  View Solution play_arrow

• question_answer134)
  The value of \[{{\cos }^{2}}0{}^\circ +{{\cos }^{2}}30{}^\circ +{{\cos }^{2}}45{}^\circ +{{\cos }^{2}}60{}^\circ +{{\cos }^{2}}90{}^\circ \] is
  A)
    \[\frac{1}{2}\]   done clear
  B)
  \[\frac{3}{2}\] done clear
  C)
  \[\frac{5}{2}\] done clear
  D)
    \[\frac{7}{2}\]   done clear
  View Solution play_arrow

• question_answer135)
  A man looks from the top of a vertical tower 30 metres high at a marked point upon the horizontal plane on which the tower stands. The angle of depression of this point is \[30{}^\circ \]. The distance of the marked point from the foot of the tower is
  A)
  \[\frac{30}{\sqrt{3}}m\] done clear
  B)
    \[\frac{30\sqrt{3}}{2}m\]   done clear
  C)
  \[30\,\,m\] done clear
  D)
  \[30\sqrt{3}\,\,m\] done clear
  View Solution play_arrow

• question_answer136)
  The least value of \[4\cos x+3\sin x\] is
  A)
  0 done clear
  B)
  2 done clear
  C)
  -3 done clear
  D)
  -5 done clear
  View Solution play_arrow

• question_answer137)
  The value of a satisfying \[6{{\sin }^{2}}\alpha -5\cos \alpha =2\] is
  A)
  \[\alpha =\frac{\pi }{2}\] done clear
  B)
  \[\alpha =\frac{\pi }{3}\] done clear
  C)
  \[\alpha =\frac{\pi }{4}\] done clear
  D)
  \[\alpha =\frac{\pi }{6}\] done clear
  View Solution play_arrow

• question_answer138)
  The smallest value of an angle whose sine \[-\frac{\sqrt{3}}{2}\] is
  A)
  \[30{}^\circ \] done clear
  B)
  \[60{}^\circ \] done clear
  C)
  \[120{}^\circ \] done clear
  D)
  \[240{}^\circ \]   done clear
  View Solution play_arrow

• question_answer139)
  A man observes the elevation of a tower to be \[30{}^\circ \]. After advancing 11 cm towards it, he finds that the elevation is \[45{}^\circ \]. The height of the tower to the nearest metre is
  A)
   10                          done clear
  B)
          15   done clear
  C)
   20                          done clear
  D)
          22 done clear
  View Solution play_arrow

• question_answer140)
  A rope of length 5 metres is tightly tied with one end at the top of a vertical pole and other end to the horizontal ground. If the rope makes an angle \[30{}^\circ \] to the horizontal, then the height of the pole is
  A)
  \[\frac{5}{2}\,m\] done clear
  B)
  \[\frac{5}{\sqrt{2}}\,m\] done clear
  C)
  \[5\sqrt{2}\,m\] done clear
  D)
  \[5\,m\] done clear
  View Solution play_arrow

• question_answer141)
  AB is a straight road leading to C, the foot of a tower. A is at a distance 200 metres from C and B at 75 metres from C. If the angle of elevation of the tower at B be double the angle of elevation at A, then the height of the tower is
  A)
   125 m                   done clear
  B)
          120 m done clear
  C)
   115m                    done clear
  D)
          100 m   done clear
  View Solution play_arrow

• question_answer142)
  If \[\cos \theta +\sin \theta =\sqrt{2}\cos \theta ,\]then value of \[r\sin \alpha \sin \beta \]is
  A)
  \[\sqrt{2}\sin \theta \] done clear
  B)
  \[\sqrt{2}co{{s}^{2}}\theta \] done clear
  C)
  \[\sqrt{2}cos\theta \] done clear
  D)
  \[\sqrt{2}si{{n}^{2}}\theta \] done clear
  View Solution play_arrow

• question_answer143)
  If \[-\frac{\pi }{4}<\theta <\frac{\pi }{4}\] then the value of \[\cos \theta -\sin \theta \] is
  A)
  always negative done clear
  B)
  always positive   done clear
  C)
  sometimes positive, sometimes negative done clear
  D)
  0 done clear
  View Solution play_arrow

• question_answer144)
  If \[\alpha \] and \[\beta \] are angles in the first quadrant \[\tan \alpha \frac{1}{7}\,\,.\,\,sin\beta =\frac{1}{\sqrt{10}}\], then the value of \[\alpha +2\beta \] is?
  A)
  \[0{}^\circ \] done clear
  B)
  \[30{}^\circ \] done clear
  C)
  \[45{}^\circ \]   done clear
  D)
   \[60{}^\circ \] done clear
  View Solution play_arrow

• question_answer145)
  The value of sin \[15{}^\circ \] is
  A)
    \[\frac{\sqrt{3}+1}{2}\] done clear
  B)
  \[\frac{\sqrt{3}+1}{2\sqrt{2}}\] done clear
  C)
    \[\frac{-(\sqrt{3}+1)}{2\sqrt{2}}\] done clear
  D)
    \[\frac{\sqrt{3}-1}{2\sqrt{2}}\] done clear
  View Solution play_arrow

• question_answer146)
  Which of the following is incorrect?
  A)
  \[{{\cos }^{4}}\theta -{{\sin }^{4}}\theta ={{\cos }^{2}}\theta -{{\sin }^{2}}\theta \] done clear
  B)
  \[1+{{\tan }^{2}}\theta ={{\operatorname{csec}}^{2}}\theta \] done clear
  C)
  \[\sin 40{}^\circ +\cos 50{}^\circ =2\sin 40{}^\circ \] done clear
  D)
  \[{{\sin }^{2}}\theta +{{\cos }^{2}}(-\theta )=-1\] done clear
  View Solution play_arrow

• question_answer147)
  \[{{(cosA+sinA)}^{2}}-{{(cosA-sinA)}^{2}}\] is equal to
  A)
  -1 done clear
  B)
  2 done clear
  C)
  0 done clear
  D)
  2 sin 2A   done clear
  View Solution play_arrow

• question_answer148)
  The value of \[\frac{\sin 4\theta }{\cos \theta }\] is
  A)
  \[4\cos \theta \,\cos 2\theta \] done clear
  B)
  \[4\sin \theta \,\cos 2\theta \] done clear
  C)
  \[4\sin \theta \,\sin 2\theta \] done clear
  D)
  \[4\cos \theta \,\sin 2\theta \] done clear
  View Solution play_arrow

• question_answer149)
  The value of \[{{\sin }^{2}}60{}^\circ \,.\,\,{{\cos }^{2}}30{}^\circ +\tan 45{}^\circ \,.\,\,\cos 60{}^\circ \,\sin 30{}^\circ \] is
  A)
  \[\frac{13}{16}\] done clear
  B)
  \[5\] done clear
  C)
  \[1\] done clear
  D)
  \[-\frac{1}{2}\] done clear
  View Solution play_arrow

• question_answer150)
  If A is the complementary of B, then value of \[\sin A-\cos B\] is
  A)
  \[1\] done clear
  B)
  \[-1\] done clear
  C)
  \[\frac{1}{2}\] done clear
  D)
  \[0\] done clear
  View Solution play_arrow

• question_answer151)
  If A, B, C and D are the angles of a quadrilateral , then sin (A + B) + sin (C + D) is equal to
  A)
  1                     done clear
  B)
  - 1 done clear
  C)
  0 done clear
  D)
  \[\frac{1}{2}\] done clear
  View Solution play_arrow

• question_answer152)
  \[\tan \theta \] is not defined when \[\theta \] is equal to
  A)
  \[0{}^\circ \] done clear
  B)
  \[\frac{\pi }{4}\] done clear
  C)
  \[\frac{\pi }{6}\] done clear
  D)
  \[\frac{\pi }{2}\] done clear
  View Solution play_arrow

• question_answer153)
  If \[\cos \alpha =\frac{3}{5}\], then the value of \[\frac{sin\alpha -\frac{1}{\tan \alpha }}{2\tan \,\,\alpha }\] is
  A)
  \[\frac{3}{160}\] done clear
  B)
  \[\frac{841}{160}\] done clear
  C)
  \[\frac{41}{160}\] done clear
  D)
  \[\frac{31}{160}\] done clear
  View Solution play_arrow

• question_answer154)
  If \[\tan \theta =\frac{8}{15}\],then the value of \[\frac{17sin\theta +\frac{5}{\cos \theta }}{5\tan \theta +\frac{8}{\sin \theta }}\]
  A)
  \[\frac{59}{41}\] done clear
  B)
  \[\frac{35}{41}\] done clear
  C)
  \[\frac{41}{59}\] done clear
  D)
  \[\frac{41}{35}\] done clear
  View Solution play_arrow

• question_answer155)
  If \[\tan \alpha =2\sqrt{2}\], then the value of \[\frac{\tan \alpha }{\frac{{{\sin }^{3}}\alpha }{\cos \alpha }+\sin \alpha \cdot \cos \alpha }\] is
  A)
  \[0\] done clear
  B)
  \[2\sqrt{2}\] done clear
  C)
  \[-2\sqrt{2}\] done clear
  D)
  \[1\] done clear
  View Solution play_arrow

• question_answer156)
  The value of \[{{(cos\alpha +sin\alpha )}^{2}}+{{(cos\alpha -sin\alpha )}^{2}}\] is
  A)
  2 done clear
  B)
  -2 done clear
  C)
  1 done clear
  D)
  0 done clear
  View Solution play_arrow

• question_answer157)
  The value of \[si{{n}^{6}}\theta +{{\cos }^{6}}\theta +3si{{n}^{2}}\theta \,.\,\,{{\cos }^{2}}\theta \] is
  A)
  0 done clear
  B)
  -1 done clear
  C)
  1 done clear
  D)
  2 done clear
  View Solution play_arrow

• question_answer158)
  The value of \[4(si{{n}^{4}}30{}^\circ +{{\cos }^{4}}60{}^\circ )-3(co{{s}^{2}}45{}^\circ -{{\sin }^{2}}90{}^\circ )\] is
  A)
  0 done clear
  B)
  1 done clear
  C)
  2 done clear
  D)
  -2 done clear
  View Solution play_arrow

• question_answer159)
  The value of sin \[18{}^\circ \] is
  A)
  \[\frac{\sqrt{5}-1}{4}\] done clear
  B)
  \[\frac{\sqrt{5}+1}{4}\] done clear
  C)
  \[-\frac{\sqrt{5}+1}{4}\] done clear
  D)
  \[\frac{1-\sqrt{5}}{4}\] done clear
  View Solution play_arrow

• question_answer160)
  Find the value of \[x\] from the equation \[x\sin \frac{\pi }{6}{{\cos }^{2}}\frac{\pi }{4}=\frac{{{\cot }^{2}}\frac{\pi }{6}\sec \frac{\pi }{3}\tan \frac{\pi }{4}}{{{\operatorname{cosec}}^{2}}\frac{\pi }{4}\operatorname{cosec}\frac{\pi }{6}}\]
  A)
  4 done clear
  B)
  6 done clear
  C)
  -2 done clear
  D)
  0 done clear
  View Solution play_arrow

• question_answer161)
  Find the value of sin \[75{}^\circ \]
  A)
  \[\frac{\sqrt{3}+1}{2\sqrt{2}}\] done clear
  B)
  \[\frac{\sqrt{3}-1}{2\sqrt{2}}\] done clear
  C)
  \[\frac{1-\sqrt{3}}{2\sqrt{2}}\] done clear
  D)
  \[\frac{\sqrt{3}+1}{2+\sqrt{2}}\] done clear
  View Solution play_arrow

• question_answer162)
  If ABCD is a cyclic quadrilateral, then find which of the following statement is not correct?
  A)
  \[\sin (A+C)=0\] done clear
  B)
  \[\sin (A+B)=0\] done clear
  C)
  \[cos(B+D)=-1\] done clear
  D)
  \[sin(A+B+\text{C}+D)=0\] done clear
  View Solution play_arrow

• question_answer163)
    The value of \[\tan 1{}^\circ \,\,\tan 2{}^\circ \,\,\tan 3{}^\circ .......\tan 89{}^\circ \] is  
  A)
  0 done clear
  B)
  1 done clear
  C)
   infinity                 done clear
  D)
  none done clear
  View Solution play_arrow

• question_answer164)
  If \[\sin \,x+{{\sin }^{2}}x=1\], then the value of \[co{{s}^{12}}\,x+3co{{s}^{10}}\,x+3co{{s}^{8}}\,x+co{{s}^{6}}\,x-1\] is
  A)
  -1 done clear
  B)
  0 done clear
  C)
  1 done clear
  D)
  2 done clear
  View Solution play_arrow

• question_answer165)
  If \[\sec \theta \,.\,\,\sin \theta =0\], then the value of \[\cos \theta \] is
  A)
  \[0\] done clear
  B)
  \[\frac{1}{2}\] done clear
  C)
  \[1\] done clear
  D)
  \[-\frac{1}{2}\] done clear
  View Solution play_arrow

• question_answer166)
  The value of \[{{(sin\theta +cosec\theta )}^{2}}+{{(cos\theta +sec\theta )}^{2}}(ta{{n}^{2}}\theta +co{{t}^{2}}\theta )\] is
  A)
  1 done clear
  B)
  2 done clear
  C)
  6 done clear
  D)
  7 done clear
  View Solution play_arrow

• question_answer167)
  The value of \[\frac{\tan \alpha }{1-\cot \alpha }+\frac{cot\alpha }{1-tan\alpha }\] is identically equal to
  A)
  \[\sec \alpha \,\cdot \,\operatorname{cosec}\alpha \] done clear
  B)
  \[\sin \alpha \,\cdot \,\cos \alpha \] done clear
  C)
  \[\sec \alpha \,\cdot \,\operatorname{cosec}\alpha +1\] done clear
  D)
  \[\sin \alpha \,\cdot \,\cos \alpha +1\] done clear
  View Solution play_arrow

• question_answer168)
  If ABC is an isosceles triangle right angled at C, then tan (A - B) is
  A)
  0 done clear
  B)
  1 done clear
  C)
  \[\infty \] done clear
  D)
  -1 done clear
  View Solution play_arrow

• question_answer169)
  In a triangle \[ABC,\,\,\tan A+\tan B+\tan C\] is equal to
  A)
  \[1\] done clear
  B)
  \[0\] done clear
  C)
  \[\tan A\,\,\tan B\,\,\tan C\] done clear
  D)
  \[-1\] done clear
  View Solution play_arrow

• question_answer170)
  The minimum value of \[{{\sec }^{2}}\alpha +{{\cos }^{2}}\alpha \] is
  A)
  1 done clear
  B)
  2 done clear
  C)
  0 done clear
  D)
  -1 done clear
  View Solution play_arrow

• question_answer171)
    If ABCD is a cyclic quadrilateral, then the value of \[\cos A+\cos B+\cos C+\cos D\] is  
  A)
  0 done clear
  B)
  -1 done clear
  C)
  1 done clear
  D)
  Cannot be found done clear
  View Solution play_arrow

• question_answer172)
  If \[\sin \alpha =\frac{1-{{x}^{2}}}{1+{{x}^{2}}}\], then the value of tan \[\alpha \] is
  A)
  \[\frac{2x}{1-{{x}^{2}}}\] done clear
  B)
  \[\frac{1-{{x}^{2}}}{2x}\] done clear
  C)
  \[\frac{1}{1+{{x}^{2}}}\] done clear
  D)
  \[\frac{1}{1-{{x}^{2}}}\] done clear
  View Solution play_arrow

• question_answer173)
  If\[\sin \beta =\frac{12}{13}\],then the value of\[\frac{13\sin \beta +5\sec \beta }{5\tan \beta +6\cos ec\beta }\]
  A)
   0                             done clear
  B)
          1 done clear
  C)
   \[\frac{50}{37}\]                                done clear
  D)
          \[\frac{37}{2}\] done clear
  View Solution play_arrow

• question_answer174)
  If\[\sec \beta =\alpha +\frac{1}{4a}\], then the value of\[\text{sec}\beta +\text{tan}\beta \]
  A)
   \[a\,or\,\frac{1}{a}\]                     done clear
  B)
  \[2a\,or\,\frac{1}{2a}\]   done clear
  C)
   \[4a\,\,or\,\frac{1}{4a}\]             done clear
  D)
  1 done clear
  View Solution play_arrow

• question_answer175)
  The difference between two angles is \[19{}^\circ \] and their sum is\[\frac{890}{9}\]grades. Find the greater angle. \[[Grade=\frac{1}{100}part\,\,of\,\,rt.angle=\left( \frac{90}{100} \right)\circ ={{0.9}^{\circ }}\]
  A)
  \[63{}^\circ \] done clear
  B)
         \[35{}^\circ \] done clear
  C)
  \[27{}^\circ \] done clear
  D)
         \[54{}^\circ \]   done clear
  View Solution play_arrow

• question_answer176)
  The angles of a quadrilateral are in A.P. and the greatest is double the least. Find the least angle in radian.
  A)
   \[\frac{\pi }{6}\]                              done clear
  B)
          \[\frac{\pi }{4}\] done clear
  C)
   \[\frac{\pi }{3}\]                                done clear
  D)
          \[\frac{\pi }{5}\] done clear
  View Solution play_arrow

• question_answer177)
  Find the minimum value of\[\text{cose}{{\text{c}}^{\text{2}}}\theta +\text{si}{{\text{n}}^{\text{2}}}\theta \].
  A)
   0                             done clear
  B)
          - 1 done clear
  C)
   1                             done clear
  D)
          2   done clear
  View Solution play_arrow

• question_answer178)
  If \[\text{cosA}=\text{2sinA},\]find the value, of cosec A.
  A)
   1                                             done clear
  B)
  \[\pm \sqrt{5}\] done clear
  C)
   \[\frac{1}{2}\]                    done clear
  D)
  \[\pm \sqrt{3}\] done clear
  View Solution play_arrow

• question_answer179)
  If \[\text{sin}\left( \text{C}+\text{D} \right)=\text{sinC}.\text{cosD}+\text{cosC}.\text{cosD}\]then the value of sin \[75{}^\circ \] is
  A)
   \[\frac{1}{2\sqrt{2}}(\sqrt{3}+1)\]             done clear
  B)
   \[\frac{1}{2}(\sqrt{3}-1)\] done clear
  C)
   \[\frac{\sqrt{3}}{2}\]                     done clear
  D)
          \[\frac{1}{2}\] done clear
  View Solution play_arrow

• question_answer180)
  In a right angled triangle ABC, right angled at C, \[tanB=\sqrt{3},then\,\,sinA+sinB\]is equal to
  A)
   \[\frac{\sqrt{3}+1}{2}\]   done clear
  B)
          \[\sqrt{3}\] done clear
  C)
   \[\frac{1}{2}\]                   done clear
  D)
          1 done clear
  View Solution play_arrow

• question_answer181)
  \[{{\left( \text{1}-\text{sinA}+\text{cosA} \right)}^{\text{2}}}\]is equal to
  A)
   \[\text{2}\left( \text{1}+\text{cosA} \right)\left( \text{1}-\text{cosA} \right)\] done clear
  B)
   \[\text{2}\left( \text{l}-\text{sinA} \right)\left( \text{l}+\text{cosA} \right)\]   done clear
  C)
   \[\text{2}\left( \text{l}+\text{sinA} \right)\left( \text{l}-\text{sin A} \right)\] done clear
  D)
  \[\text{2}\left( \text{l}+\text{sinA} \right)\left( \text{l}-\text{cosA} \right)\] done clear
  View Solution play_arrow

• question_answer182)
  \[\left( \text{1}-\text{si}{{\text{n}}^{\text{2}}}\theta  \right)\left( \text{1}+\text{ta}{{\text{n}}^{\text{2}}}\theta  \right)\]is equal to
  A)
   3                             done clear
  B)
          2 done clear
  C)
   1                               done clear
  D)
          0 done clear
  View Solution play_arrow

• question_answer183)
  \[\frac{\cos A}{1-\tan A}+\frac{\sin A}{1-\cot A}\]is equal to
  A)
  \[\text{sinA}-\text{cosA}\]      done clear
  B)
          sin A + cos A   done clear
  C)
  \[\text{1 }-\text{ cos A}\]          done clear
  D)
          \[\text{1}-\text{ sin A}\] done clear
  View Solution play_arrow

• question_answer184)
  \[\frac{\text{1}-\text{sin A}}{\cos A}\]is equal to
  A)
   \[\frac{\cos A}{1+\sin A}\]            done clear
  B)
          \[\frac{\sin A}{1-\cos A}\] done clear
  C)
   \[\frac{\tan A}{1+\tan A}\]         done clear
  D)
          \[\frac{\tan A}{1+\cos A}\] done clear
  View Solution play_arrow

• question_answer185)
  If \[\cos \theta =\frac{2}{3}\] and \[\theta \] is in the 4th quadrant, then\[\frac{\sin \theta +\tan \theta }{\sin \theta -\tan \theta }\] is equal to  
  A)
   \[-\frac{1}{5}\]                 done clear
  B)
   \[\frac{1}{5}\] done clear
  C)
   \[-5\]                                      done clear
  D)
  5 done clear
  View Solution play_arrow

• question_answer186)
  The lengths of diagonals of a rhombus bear the ratio \[1:\sqrt{3}\]. The angles of the rhombus are
  A)
  \[30{}^\circ ,\text{ }60{}^\circ \] done clear
  B)
  \[30{}^\circ ,\text{ }120{}^\circ \] done clear
  C)
  \[60{}^\circ ,\text{ }120{}^\circ \]   done clear
  D)
  \[90{}^\circ ,\text{ }120{}^\circ \] done clear
  View Solution play_arrow

• question_answer187)
  The angle of elevation of the top of a lamp-post as observed from a point 40 m distant from the foot of the post, is \[30{}^\circ \]. The height of the lamp post is
  A)
   \[40\sqrt{3}m\]           done clear
  B)
  \[\frac{40\sqrt{3}}{3}m\]   done clear
  C)
  \[20 m\] done clear
  D)
  \[\frac{40\sqrt{3}}{2}m\]  done clear
  View Solution play_arrow

• question_answer188)
  If \[\text{sin}\theta =\frac{7}{25}\] and \[\theta \] lies in the second quadrant, then the value of  \[\text{sec}\theta +\text{tan}\theta \] is
  A)
   \[-\frac{4}{3}\]                   done clear
  B)
  \[-\frac{3}{4}\] done clear
  C)
  \[-\frac{2}{3}\]                done clear
  D)
  \[-\frac{1}{3}\] done clear
  View Solution play_arrow

• question_answer189)
  The value of \[\text{4co}{{\text{s}}^{\text{2}}}\text{6}0{}^\circ +\text{4ta}{{\text{n}}^{\text{2}}}\text{45}{}^\circ -\text{cose}{{\text{c}}^{\text{2}}}\text{3}0{}^\circ \] is
  A)
   0            done clear
  B)
                          2 done clear
  C)
   1                               done clear
  D)
          \[\frac{1}{2}\] done clear
  View Solution play_arrow

• question_answer190)
  The value of cos \[(-\text{ }840{}^\circ )\] is
  A)
   \[\frac{\sqrt{3}}{2}\]     done clear
  B)
                          \[-\frac{1}{2}\]   done clear
  C)
   \[\frac{1}{\sqrt{2}}\]                     done clear
  D)
          \[\frac{1}{2}\] done clear
  View Solution play_arrow

• question_answer191)
  In the given figure, the side PQ (in cm) is
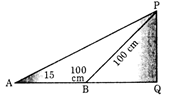
  A)
   25                          done clear
  B)
          50   done clear
  C)
   75                          done clear
  D)
          80 done clear
  View Solution play_arrow

• question_answer192)
  Which one of the following is the shadow of a two meter high post on a horizontal plane through its foot, when the altitude of the sum is \[30{}^\circ \]?
  A)
   \[3\sqrt{3}\,m\]              done clear
  B)
          \[\sqrt{7}\,m\] done clear
  C)
   \[2\sqrt{3}\,m\]                                done clear
  D)
   \[\frac{1}{\sqrt{3}}\,m\] done clear
  View Solution play_arrow

• question_answer193)
  The area of a triangle is 12 sq. cm. Two sides are 6 cm and 12 cm. The included angle is
  A)
   \[{{\cos }^{-1}}\left( \frac{1}{3} \right)\]               done clear
  B)
          \[{{\cos }^{-1}}\left( \frac{1}{6} \right)\] done clear
  C)
   \[{{\sin }^{-1}}\left( \frac{1}{6} \right)\]                done clear
  D)
          \[{{\sin }^{-1}}\left( \frac{1}{3} \right)\]   done clear
  View Solution play_arrow

• question_answer194)
  A man observes the elevation of a balloon to be \[30{}^\circ \]. He then walks 1 km. towards the balloon and finds the angle of elevation now is \[60{}^\circ \]. The height (in km) of the balloon is
  A)
   \[\frac{\sqrt{3}}{2}\]                       done clear
  B)
          \[\sqrt{3}+1\] done clear
  C)
   \[\sqrt{3}-1\]    done clear
  D)
          \[\frac{2}{\sqrt{3}}\] done clear
  View Solution play_arrow

• question_answer195)
  The value of\[\text{sin45}{}^\circ \text{cos45}{}^\circ {{\left( \text{tan45}{}^\circ +\text{cot45}{}^\circ  \right)}^{\text{2}}}\]is
  A)
   1                             done clear
  B)
          2   done clear
  C)
   3                             done clear
  D)
          4 done clear
  View Solution play_arrow

• question_answer196)
  The value of \[x\] from the equation\[\frac{x}{\cos {{45}^{\circ }}.\sin {{60}^{\circ }}}={{\tan }^{2}}{{60}^{\circ }}-{{\tan }^{2}}{{30}^{\circ }}\], is
  A)
   3                             done clear
  B)
          2 done clear
  C)
   1                             done clear
  D)
          None of these   done clear
  View Solution play_arrow

• question_answer197)
  The value of\[\text{sec}\left( \text{9}{{0}^{\circ }}-\theta  \right)\text{sin}\theta \], is
  A)
  \[\text{sec }\theta \]                     done clear
  B)
          \[\text{cosec }\theta \] done clear
  C)
  \[\text{tan }\theta \]                     done clear
  D)
          1   done clear
  View Solution play_arrow

• question_answer198)
  Find the value of \[\sin 22{}^\circ \cos 38{}^\circ +\cos 22{}^\circ \sin 38{}^\circ \].
  A)
   \[\frac{1}{2}\]                                   done clear
  B)
   \[-\frac{\sqrt{3}}{2}\] done clear
  C)
   \[\frac{\sqrt{3}}{2}\]                       done clear
  D)
          \[\frac{1}{\sqrt{2}}\] done clear
  View Solution play_arrow

• question_answer199)
  The angle of elevation of the top of a tower at a distance of\[\frac{50\sqrt{3}}{3}\] metres from the foot is \[60{}^\circ \]. Find the height of the tower.
  A)
   \[50\sqrt{3}\]metres                     done clear
  B)
   \[\frac{20}{\sqrt{3}}\] metres done clear
  C)
   \[-50\]metres      done clear
  D)
          50 metres   done clear
  View Solution play_arrow

• question_answer200)
  Find the value of\[\text{cos}\theta -\text{cos3}\theta +\text{cos4}\theta \], when\[\theta =45{}^\circ \] .
  A)
  \[\frac{\sqrt{3}}{2}\] done clear
  B)
  \[\sqrt{3}-1\] done clear
  C)
    \[\frac{1}{2}\]   done clear
  D)
  \[\sqrt{2}-1\] done clear
  View Solution play_arrow

• question_answer201)
  Value of the expression \[\left( \text{1}-\text{cos}\theta  \right)\left( \text{1}+\text{cos}\theta  \right)\left( \text{1}+\text{co}{{\text{t}}^{\text{2}}}\theta  \right)\]is
  A)
   0                             done clear
  B)
          1   done clear
  C)
   \[{{\sin }^{2}}\theta \]  done clear
  D)
          \[\cos e{{c}^{2}}\theta \] done clear
  View Solution play_arrow

• question_answer202)
  The value of \[\text{cos2}0{}^\circ \text{ }.\text{ cos4}0{}^\circ \text{ }.\text{ cos6}0{}^\circ .\text{ cos8}0{}^\circ \]is
  A)
   \[\frac{1}{2}\]   done clear
  B)
                          \[\frac{1}{4}\] done clear
  C)
   \[\frac{1}{8}\]                   done clear
  D)
          \[\frac{1}{16}\]   done clear
  View Solution play_arrow

• question_answer203)
  On the level ground, the angle of elevation of the top of a tower is \[30{}^\circ \]. On moving 20 metres nearer to it the angle of elevation is \[60{}^\circ \]. The height of the tower is
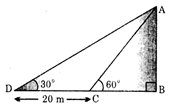
  A)
   10 mts           done clear
  B)
          15 mts done clear
  C)
   20 mts                  done clear
  D)
          \[10\sqrt{3}\] mts   done clear
  View Solution play_arrow

• question_answer204)
  The value of\[\frac{\cos \theta }{\sin (90+\theta )}+\frac{\sin (-\theta )}{\sin (180+\theta )}+\frac{\tan (90+\theta )}{\cot \theta }\] is
  A)
  0 done clear
  B)
  1 done clear
  C)
  2 done clear
  D)
  -2 done clear
  View Solution play_arrow

• question_answer205)
  If \[\alpha \] and \[\beta \] are angles in the first quadrant, \[\tan \alpha =\frac{1}{7},\sin \beta =\frac{1}{\sqrt{10}}\], then using the formula \[\text{sin}\left( \text{A}+\text{B} \right)=\text{sinAcosB}+\text{cosAsinB}\], the value of \[\left( \alpha +\text{2}\beta  \right)\] is
  A)
  \[0{}^\circ \] done clear
  B)
  \[45{}^\circ \]   done clear
  C)
  \[60{}^\circ \] done clear
  D)
  \[90{}^\circ \] done clear
  View Solution play_arrow

• question_answer206)
  If \[\alpha +\beta =\text{9}0{}^\circ \] and \[\alpha =2\beta \], then \[\text{co}{{\text{s}}^{\text{2}}}\alpha +\text{si}{{\text{n}}^{\text{2}}}\beta \] equals to
  A)
  \[\frac{1}{2}\]                    done clear
  B)
  0 done clear
  C)
  1 done clear
  D)
  2 done clear
  View Solution play_arrow