Trigonometric Ratio of Sub-multiple of an Angle
Category : JEE Main & Advanced
(1) \[\left| \,\sin \frac{A}{2}+\cos \frac{A}{2}\, \right|=\sqrt{1+\sin A}\]
or \[\sin \frac{A}{2}+\cos \frac{A}{2}=\pm \sqrt{1+\sin A}\]
i.e., \[\left\{ \begin{matrix} +,\,\text{If }2n\pi -\pi /4\le A/2\le 2n\pi +\frac{3\pi }{4} \\ -,\,\text{otherwise}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \\ \end{matrix} \right.\]
(2) \[\left| \,\sin \frac{A}{2}-\cos \frac{A}{2}\, \right|=\sqrt{1-\sin A}\]
or \[(\sin \frac{A}{2}-\cos \frac{A}{2})=\pm \sqrt{1-\sin A}\]
i.e., \[\left\{ \begin{matrix} +,\,\text{If }2n\pi +\pi /4\le A/2\le 2n\pi +\frac{5\pi }{4} \\ -,\,\text{otherwise}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \\ \end{matrix} \right.\]
(3) (i) \[\tan \frac{A}{2}=\frac{\pm \sqrt{{{\tan }^{2}}A+1}-1}{\tan A}=\pm \,\sqrt{\frac{1-\cos A}{1+\cos A}}=\frac{1-\cos A}{\sin A}\],
where \[A\ne (2n+1)\pi \]
(ii) \[\cot \frac{A}{2}=\pm \,\sqrt{\frac{1+\cos A}{1-\cos A}}=\frac{1+\cos A}{\sin A}\], where \[A\ne 2n\pi \]
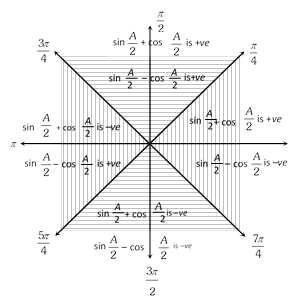
The ambiguities of signs are removed by locating the quadrants in which \[\frac{A}{2}\] lies or you can follow the following figure,
(4) \[{{\tan }^{2}}\frac{A}{2}=\frac{1-\cos A}{1+\cos A}\] ; where \[A\ne (2n+1)\pi \] (5) \[{{\cot }^{2}}\frac{A}{2}=\frac{1+\cos A}{1-\cos A}\]; where \[A\ne 2n\pi \]
You need to login to perform this action.
You will be redirected in
3 sec
