Theorem of The Medians: (Apollonius Theorem)
Category : JEE Main & Advanced
In every triangle the sum of the squares of any two sides is equal to twice the square on half the third side together with twice the square on the median that bisects the third side.
For any triangle ABC, \[{{b}^{2}}+{{c}^{2}}=2({{h}^{2}}+{{m}^{2}})=2\{{{m}^{2}}+{{(a/2)}^{2}}\}\] by use of cosine rule.
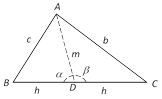
If \[\Delta \] be right angled, the mid point of hypotenuse is equidistant from the three vertices so that \[DA=DB=DC\].
\[\therefore {{b}^{2}}+{{c}^{2}}={{a}^{2}}\] which is pythagoras theorem. This theorem is very useful for solving problems of height and distance.
You need to login to perform this action.
You will be redirected in
3 sec
