Some Terminology Related to Height and Distance
Category : JEE Main & Advanced
(1) Angle of elevation and depression: Let O and P be two points such that P is at higher level than O. Let PQ, OX be horizontal lines through P and O, respectively. If an observer (or eye) is at O and the object is at P, then \[\angle XOP\] is called the angle of elevation of P as seen from O. This angle is also called the angular height of P from O.

If an observer (or eye) is at P and the object is at O, then \[\angle QPO\] is called the angle of depression of O as seen from P.
(2) Method of solving a problem of height and distance
(i) Draw the figure neatly showing all angles and distances as far as possible.
(ii) Always remember that if a line is perpendicular to a plane then it is perpendicular to every line in that plane.
(iii) In the problems of heights and distances we come across a right angled triangle in which one (acute) angle and a side is given. Then to find the remaining sides, use trigonometrical ratios in which known (given) side is used, i.e., use the formula.
(iv) In any triangle other than right angled triangle, we can use 'the sine rule'.
i.e., formula, \[\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C},\] or cosine formula i.e., \[\cos A=\frac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc}\] etc.
(v) Find the length of a particular side from two different triangles containing that side common and then equate the two values thus obtained.
(3) Geometrical properties and formulae for a triangle
(i) In a triangle the internal bisector of an angle divides the opposite side in the ratio of the arms of the angle. \[\frac{BD}{DC}=\frac{c}{b}\].
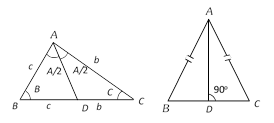
(ii) In an isosceles triangle the median is perpendicular to the base i.e., \[AD\,\bot \,BC\].
(iii) In similar triangles the corresponding sides are proportional.
(iv) The exterior angle is equal to sum of interior opposite angles.
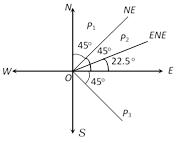
(4) North-east : North-east means equally inclined to north and east, south-east means equally inclined to south and east. ENE means equally inclined to east and north-east.
(5) Bearing : In the figure, if the observer and the object i.e., O and P be on the same level then bearing is defined. To measure the ?Bearing?, the four standard directions East, West, North and South are taken as the cardinal directions.
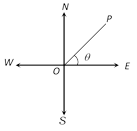
Angle between the line of observation i.e., OP and any one standard direction– east, west, north or south is measured.
Thus, \[\angle POE=\theta \] is called the bearing of point P with respect to O measured from east to north. In other words the bearing of P as seen from O is the direction in which P is seen from O.
(6) \[\mathbf{m-n}\] cot theorem of trigonometry : \[(m+n)\] \[\cot \theta \] \[=m\cot \alpha -n\cot \beta =n\cot A-m\cot B\] (\[\theta \] on the right)
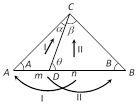
If \[\theta \] is on the left then angle in the right is \[\pi -\theta \] and \[\cot \left( \pi -\theta \right)=-\cot \theta \]. Hence in this case \[m-n\] theorem becomes \[-(m+n)\cot \theta =m\cot \alpha -n\cot \beta \] \[=n\cot A-m\cot B\] (\[\theta \] on the left).
You need to login to perform this action.
You will be redirected in
3 sec
