Relation Between Sides and Angles
Category : JEE Main & Advanced
A triangle has six components, three sides and three angles. The three angles of a \[\Delta ABC\] are denoted by letters \[A,\,\,B,\,\,C\] and the sides opposite to these angles by letters \[a,\,\,b\] and \[c\] respectively. Following are some well known relations for a triangle (say \[\Delta ABC\])
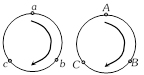
Generally, the relations involving the sides and angles of a triangle are cyclic in nature, e.g. to obtain the second similar relation to \[a+b>c,\] we simply replace \[a\] by \[b,\,\,b\] by \[c\] and \[c\] by \[a\]. So, to write all the relations, follow the cycles given.
The law of sines or sine rule : The sides of a triangle are proportional to the sines of the angles opposite to them i.e., \[\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=k,\,(say)\]
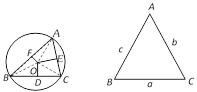
More generally, if \[R\] be the radius of the circumcircle of the triangle \[ABC,\,\,\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R\].
You need to login to perform this action.
You will be redirected in
3 sec
