JEE Main & Advanced Mathematics Trigonometric Equations Pedal Triangle

Let the perpendiculars AD, BE and CF from the vertices A, B and C on the opposite sides BC, CA and AB of \[\Delta ABC\] respectively, meet at O. Then O is the orthocentre of the \[\Delta ABC\]. The triangle DEF is called the pedal triangle of the \[\Delta ABC\].

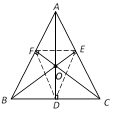
Othocentre of the triangle is the incentre of the pedal triangle.

If O is the orthocentre and DEF the pedal triangle of the \[\Delta ABC\], where AD, BE, CF are the perpendiculars drawn from A, B, C on the opposite sides BC, CA, AB respectively, then

(i)   \[OA=2R\cos A,OB=2R\cos B\]and \[OC=2R\cos C\]

(ii) \[OD=2R\cos B\cos C,OE=2R\cos C\cos A\] and \[OF=2R\cos A\cos B\]

(1) Sides and angles of a pedal triangle: The angles of pedal triangle DEF are: \[180-2A,\,180-2B,\,180-2C\] and sides of pedal triangle are:

\[EF=a\cos A\] or \[R\sin 2A\]; \[FD=b\cos B\] or \[R\sin 2B\]; \[DE=c\cos C\] or \[R\sin 2C\]

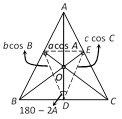
 If given \[\Delta ABC\] is obtuse, then angles are represented by \[2A,\] \[2B\], \[2C-{{180}^{o}}\] and the sides are \[a\cos A,\,\,b\cos B,\,\,-\,\,c\cos C\].

(2) Area and circum-radius and in-radius of pedal triangle : Area of pedal triangle \[=\frac{1}{2}(\text{Product of the sides)}\times \] (sine of included angle)

\[\Delta =\frac{1}{2}{{R}^{2}}.\sin 2A.\sin 2B.\sin 2C\]

Circum-radius of pedal triangle\[=\frac{EF}{2\sin FDE}=\frac{R\sin 2A}{2\sin ({{180}^{o}}-2A)}=\frac{R}{2}\]

In-radius of pedal triangle \[=\frac{\text{area of }\Delta DEF}{\text{semi-perimeter of }\Delta DEF}\]

\[=\frac{\frac{1}{2}{{R}^{2}}\sin 2A.\sin 2B.\sin 2C}{2R\sin A.\sin B.\sin C}=2R\cos A.\cos B.\cos C\]