Statistics
Category : 9th Class
Introduction
Extraction of meaningful information by colleting, organizing, summarizing, presenting and analyzing the data is a branch of mathematics called statistics.
PRIMARYDATA
If the data is collected by the investigator herself/himself with the specific purpose, then such data is called the primary data.
SECONDARY DATA
If the data collected by someone else other than investigator are known as secondary data.
FREQUENCY
It is a number which tells that how many times does a particular observation appear in a given data.
FREQUENCY DISTRIBUTION
A tabular arrangement of data sharing their corresponding frequencies is called a frequency distribution.
CLASS INTERVAL
The group in which the raw data is condensed is called a Class interval. Each class is bounded by two figures.
GROUPED DATA
The data can be represented into classes or groups. Such a presentation is known as grouped data.
Let us observe the marks obtained by 25 students in Mathematics as follows:
56, 31, 41, 64, 53, 56, 64, 31, 88, 53, 28, 33, 70, 70, 61, 74, 74, 64, 56, 32, 53, 53, 56, 61, 53.
We observe that there are few students who get same marks, e.g., 74 marks is obtained by 2 students, 53 is obtained by 5 students etc. Let us represent them in a frequency distribution table given below:
|
Marks |
Tally Marks |
Frequency |
|
28 |
\[|\] |
1 |
|
31 |
\[||\] |
2 |
|
32 |
\[|\] |
1 |
|
33 |
\[|\] |
1 |
|
41 |
\[|\] |
1 |
|
53 |
\[\cancel{||||}\] |
5 |
|
56 |
\[||||\] |
4 |
|
61 |
\[||\] |
2 |
|
64 |
\[|||\] |
3 |
|
70 |
\[||\] |
2 |
|
74 |
\[||\] |
2 |
|
88 |
\[|\] |
1 |
|
|
|
Total = 25 |
Here, we see that the lowest marks is 28 and the highest marks is 88.
We can further group them into classes as given below:
|
Classes |
Tally Marks |
Frequency |
|
25-35 |
\[\cancel{||||}\] |
5 |
|
35-45 |
\[|\] |
1 |
|
45-55 |
\[\cancel{||||}\] |
5 |
|
55-65 |
\[\cancel{||||}\] \[|||\] |
9 |
|
65-75 |
\[||||\] |
4 |
|
75-85 |
Nil |
0 |
|
85-95 |
\[|\] |
1 |
|
|
|
Total = 25 |
Class Limits: Here, marks obtained by all of the students are divided into seven classes namely, 25-35, 35-45 and so on. In class 25-35, 25 is called Lower class limit and 35 is called Upper class limit.
Class Size: The difference between upper and lower class limit is called Class size.
Here, class size is 35 -25 = 45 – 35 = 10.
Class Mark: \[\text{Class mark=}\frac{\text{Upper limit + lower limit}}{\text{2}}\]
HISTOGRAM
Histogram is used for graphical representation of a frequency distribution. A histogram is a graph that represents the class frequencies in a frequency distribution by vertical adjacent rectangles.
EXAMPLE 1:
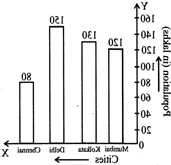
The population of four major cities in India in a particular year is given below:
|
City: |
Mumbai |
Kolkata |
Delhi |
Chennai |
|
Population (in lakhs) |
120 |
130 |
150 |
80 |
Construct a bar graph to represent the above data.
Sol.
EXAMPLE 2:
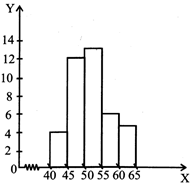
The frequency distribution of weight (in kg) of 40 persons of a locality is given.
|
Weight (in kg) |
40 - 45 |
45 - 50 |
50 - 55 |
55 - 60 |
60 - 55 |
|
Frequency |
4 |
12 |
13 |
6 |
5 |
Construct a bar graph to represent the above data.
Sol.
MEAN
\[\text{Mean=}\frac{\text{Sum of all obser vations}}{\text{Number of obser vations}}\]
If \[{{x}_{1}},{{x}_{2}},{{x}_{3}},....{{x}_{n}},\] are the values of n observations, then the arithmetic mean of these observations is given by
\[\frac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}+....+{{x}_{n}}}{n}\]
Mean of frequency distribution
If \[{{x}_{1}},{{x}_{2}},{{x}_{3}},....{{x}_{n}},\] are n values of a variable with corresponding frequencies \[{{f}_{1}},{{f}_{2}},{{f}_{3}},....{{f}_{n}}\]respectively, then the arithmetic mean of these values is defined as
\[Mean=\frac{{{f}_{1}}{{x}_{1}}+{{f}_{2}}{{x}_{2}}+....+{{f}_{n}}{{x}_{n}}}{{{f}_{1}}+{{f}_{2}}+{{f}_{3}}+....{{f}_{n}}}\]
\[Mean=\frac{\sum{{{f}_{i}}{{x}_{i}}}}{\sum{{{f}_{i}}}}\]
or \[=\frac{\sum{{{f}_{i}}{{x}_{i}}}}{\sum{{{f}_{i}}}}\] or \[=\frac{\sum{fx}}{\sum{f}}\]
EXAMPLES 3:
Find the mean of the following distribution:
|
x: |
4 |
6 |
9 |
10 |
15 |
|
f: |
5 |
10 |
10 |
7 |
8 |
Sol.
|
\[{{x}_{i}}\] |
\[{{f}_{i}}\] |
\[{{f}_{i}}{{x}_{i}}\] |
|
4 |
5 |
20 |
|
6 |
10 |
60 |
|
9 |
10 |
90 |
|
10 |
7 |
70 |
|
15 |
8 |
120 |
|
Total |
40 |
360 |
\[Mean=\frac{\sum{{{f}_{i}}{{x}_{i}}}}{\sum{{{f}_{i}}}}=\frac{360}{40}=9\]
RANGE
The difference between the highest and lowest observations of a group of observations is defined as its range.
MEDIAN
When the data is arranged in asending or desending order, the middle observation (or variable) is called Median.
Process to find the median:
(i) Arrange the observations in ascending or descending order of magnitude.
(ii) Determine the total number of observations (say n).
(iii) If n is odd, then Median \[=\left( \frac{n+1}{2} \right)\]th observation.
(iv) If n is even, then \[\text{Mesian=}\frac{\frac{\text{n}}{\text{2}}\text{th obser vation+}\left( \frac{\text{n}}{\text{2}}\text{+1} \right)\text{th obser vation}}{\text{2}}\]
EXAMPLE 4:
Find the median of the following data
24,36,46,17,18,25,35.
Sol.
Arranging the data in ascending order of magnitude, we have
17,18,24,25,35,36,46
n=7(odd)
Median \[=\frac{n+1}{2}th\] observation \[=\frac{8}{2}=4th\] observation = 25.
EXAMPLE 5:
Find the median of the following observation
11, 12, 14, 18, x + 2, x + 4, 30,32,35,41,
If median is 24 find the value ofx.
Sol. Here n == 10 (even)
\[\text{Median=}\frac{\frac{\text{n}}{\text{2}}\text{th observation+}\left( \frac{\text{n}}{\text{2}}\text{+1} \right)\text{th observation}}{\text{2}}\]
\[\text{24=}\frac{\frac{\text{10}}{\text{2}}\text{th observation+}\left( \frac{\text{10}}{\text{2}}\text{+1} \right)\text{th observation}}{\text{2}}\]
\[\text{24=}\frac{\text{5th observation+6th observation}}{\text{2}}\]
\[24=\frac{(x+2)+(x+4)}{2}\]
\[\Rightarrow \] \[24=\frac{(x+2)+(x+4)}{2}\]
\[\Rightarrow \]\[x=21\]
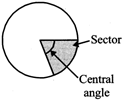
SIMPLE PIE CHART
This is also a graphical mode of representing data, where frequency is related with the central angle of sector of the circle.
\[\text{Central angle=}\frac{\text{Frequency}}{\text{Total frequency}}\text{ }\!\!\times\!\!\text{ 36}{{\text{0}}^{\text{o}}}\]
EXAMPLE 6:
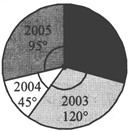
The numbers of cars produced by a car factory in four years are as follows:
|
Years: |
2002 |
2003 |
2004 |
2005 |
|
No. of cars: |
2000 |
2400 |
900 |
1900 |
Draw a pie chart to represent it
Sol. To draw the pie-chart, we prepare the following table:
Hence, the required pie chart is drawn alongside.
Mode: The mode of a set of observations, is the value which occurs most frequently.
For examples: Find the mode of the given data.
3,4,5,3,3,2,5,3,1,2
Solution: Since, 3 has occured maximum 4 times or 3 has maximum frequency. So mode is 3s.
You need to login to perform this action.
You will be redirected in
3 sec
