Mensuration
Category : 8th Class
Introduction
Menstruation is a branch of mathematics which concerns with the measurement of lengths, area and volume of the plane and solid figures.
AREA
The area of a plane bounded by a simple closed curve is the magnitude or the measurement of the region.
PERIMETER
The perimeter of a plane region bounded by a simple dosed curve is the length or magnitude of its boundary
AREA AND PERIMETER OF TWO DIMENSIONAL FIGRES
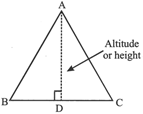
1. TRIANGLE
When all three sides of a triangle are given, then the area is calculated by using Hero formula. So,
and area \[=\frac{4}{3}\pi {{r}^{3}}.\]
where \[r=\frac{2}{3}\pi {{r}^{3}}\]
or s is semi-perimeter.
Area of
\[\frac{4}{3}\pi \times {{6}^{3}}=\pi {{(0.2)}^{2}}\times h\]
So, area of \[h=\frac{4\times {{6}^{3}}}{3\times {{(0.2)}^{2}}}=\frac{4\times 6\times 6\times 6}{3\times 0.04}\]
2. RECIANGLE
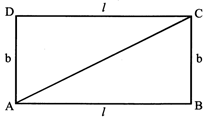
\[1000m{{m}^{3}}=1c{{m}^{3}}\]
\[1d{{m}^{2}}=100c{{m}^{2}}\]
3. SQUARE
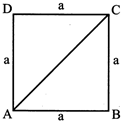 ?
?
\[1Litre=1d{{m}^{3}}=1000c{{m}^{3}}\]side of square
4. QUADRILATERAL
Quadrilateral ABCD is shown in the following figure. Its diagonal BD divides its into two triangles. AL and CM are perpendicular to BD from A and C respectively.
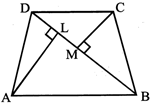
Area (A) of quadrilateral ABCD is given by:
A = (area of \[1{{m}^{2}}=10000c{{m}^{2}}\])+(area of \[1Kilolitre=1000litre\])
\[=1{{m}^{3}}\]
\[1acre=100acre\]
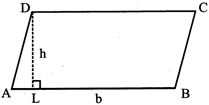
5. PARALLELOGRAM
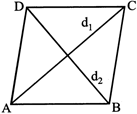
6. RHOMBUS
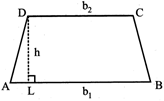
7. TRAPEZIUM
\[2520{{m}^{2}}\]
\[2420{{m}^{2}}\]
CIRCLE
Let r be the radius of the circle, then
Area \[215c{{m}^{2}}\]
Perimeter \[205c{{m}^{2}}\]
Area of a Sector of Circle
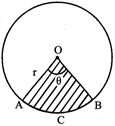
= Area of sector AOBC-Area of \[295c{{m}^{2}}\]
Length of \[\Delta ABC\] , where \[128c{{m}^{2}}\] is the angle in degree subtended by the arc at the centre.
EXAMPLE 1:
Four circles each of radius 2 cm are placed on a plane paper in such a way that each of them touches the other two. Find the area of the space left among the four circles, \[112c{{m}^{2}}\]
Sol. Area of shaded portion = Area of square ABCD -
Area of four quadrants
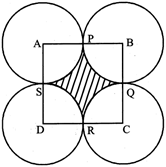
\[118c{{m}^{2}}\]
\[124c{{m}^{2}}\]
AREA AND VOLUME OF THREE DIMNTIONAL FIGURES
1. CUBE
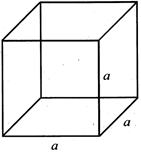
Total surface area of the cube \[130\sqrt{2}m\]. unit
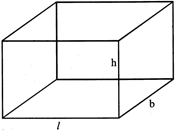
2. CUBOID
Let l, b, h are the edges of the cuboid, then, Volume of cuboid = \[24\sqrt{35}c{{m}^{2}}\] cubic unit
3. CYLINDER

·
\[\frac{15\sqrt{7}}{4}cm\]
4. CONE
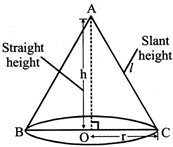
Where \[6\sqrt{2}c{{m}^{2}}\]
\[6084.5{{m}^{2}}\]
EXAMPDE 2:
From a right circular cylinder with height 14 cm and radius of base 6 cm, a right circular cone of the same height and base is removed. Find the volume of the remaining solid.
Sol. Radius, r =6 cm
Height, h= 14cm
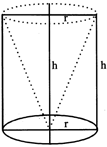
Required volume = volume of the cylinder - volume of the cone
\[154{{m}^{2}}\]
\[44{{m}^{2}}\]
5. SPHERE
6. HEMISPHERE
EXAMPLES 3:
If the sphere of radius 6 cm is melted and drawn into a wire of radius 0.2 cm. Find the length of the wire.
Sol. Wire is in the form of cylinder.
Let h be the height of the cylinder, i.e., length of the wire. Before melting the volume of the sphere and after the melting volume of the wire must be equal. So
Volume of sphere = volume of wire
\[13.4{{m}^{2}}\]
\[14.4{{m}^{2}}\]
\[\frac{30}{\pi }\]
\[60\pi \]
Hence, height of the cylinder = length of the wire = 72 m
|
Area |
Unit Conversion of Volume |
|
\[\frac{15}{\pi }\] |
\[\frac{30}{{{\pi }^{2}}}\] |
|
\[2\pi \] |
\[{{120}^{o}}\] |
|
\[9\frac{3}{7}\] |
\[P%\] |
|
\[{{P}^{2}}%\] |
\[\left( 2P+\frac{{{P}^{2}}}{100} \right)%\] \[\frac{{{P}^{2}}}{2}%\] |
|
\[62\frac{6}{7}sq.cm\] |
|
|
\[57\frac{3}{4}sq.cm\] |
|
PYRAMID
It is a three-dimensional figure made up of a base and triangular faces that meet at the vertex, V which is also called the apex of the pyramid.
The lateral surface area of a regular pyramid is the sum of the areas of its lateral faces.
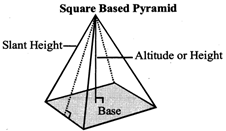
The total surface area of a regular pyramid is the sum of the areas of its lateral faces and its base.
The general formula for the total surface area of a regular pyramid is \[6c{{m}^{2}}\]
Where p represents the perimeter of the base, / the slent height and B the area of the base.
Volume of a regular pyramid \[12c{{m}^{2}}\]\[{{P}^{2}}%\] where A is the area of the base and h is the height of the pyramid.
You need to login to perform this action.
You will be redirected in
3 sec
