Surface Area of Frustum
Category : 8th Class
It is the figure obtained by cutting the cone by a plane parallel to the base of the cone, then the portion between the plane and the base is known as the frustum of the cone.
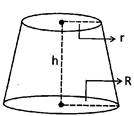
The curved surface area of frustum\[=\pi l(R+r)\]
Where, \[{{l}^{2}}={{h}^{2}}+{{(R-r)}^{2}}\].
Total surface area of the frustum \[\pi =({{R}^{2}}+{{r}^{2}}+l(R+r)\]
Volume of the frustum \[=\frac{1}{3}\pi h({{R}^{2}}+{{r}^{2}}+Rr)\]

![]()

![]() The guest room of Mary's flat is in the form of rectangle. If the width of the room is three fourth of its length and its area is given as 600\[{{\text{m}}^{\text{2}}}\]. The difference between the length and width of the room is:
The guest room of Mary's flat is in the form of rectangle. If the width of the room is three fourth of its length and its area is given as 600\[{{\text{m}}^{\text{2}}}\]. The difference between the length and width of the room is:
(a) \[5\sqrt{2}\,m\]
(b) \[7\sqrt{2}\,m\]
(c) \[9\sqrt{2}\,m\]
(d) \[3\sqrt{2}\,m\]
(e) None of these
Answer: (a)
Explanation:
Let the length of the room \[=x\].
Then the width of the room \[=\frac{3}{4}x\]
Area of the room \[=\frac{3}{4}{{x}^{2}}\]
But the area of the room \[~=\text{6}00\,{{\text{m}}^{\text{2}}}\]
Therefore, \[x=\text{6}00{{\text{m}}^{\text{2}}}\]
\[x=\sqrt{800}=20\sqrt{2}\]
![]() The ratio between the length and breath of a field is 10 : 6. The area of the field is 3840 m2. Find the difference between the length and width of the field.
The ratio between the length and breath of a field is 10 : 6. The area of the field is 3840 m2. Find the difference between the length and width of the field.
(a) 32m
(b) 24m
(c) 20m
(d) 18m
(e) None of these
Answer: (a)
Explanation:
Let the length of the field be \[10x\] and breath be \[6x\].
Then the area of the field \[=10x\times 6x=60{{x}^{2}}\]
Therefore, \[\text{6}0{{x}^{2}}=\text{384}0\] \[x=8\,m\]
Therefore, length of the field = 80 m and breath of the field = 48 m
Difference \[=\text{8}0-\text{48}=\text{32 m}\]
![]() A room of the hall is such that the ratio of the height of the room to its semi perimeter is 6 : 10 and the cost of paper wall of the room to cover the wall of the room is Rs. 1700, when the width of the paper is 100 cm at the rate of Rs. 10 per meter, except the door and window whose area is \[\text{4}0\text{ }{{\text{m}}^{\text{2}}}\]. The height of the room is:
A room of the hall is such that the ratio of the height of the room to its semi perimeter is 6 : 10 and the cost of paper wall of the room to cover the wall of the room is Rs. 1700, when the width of the paper is 100 cm at the rate of Rs. 10 per meter, except the door and window whose area is \[\text{4}0\text{ }{{\text{m}}^{\text{2}}}\]. The height of the room is:
(a) \[2\sqrt{6}\,m\]
(b) \[3\sqrt{3.5}\,m\]
(c) \[4\sqrt{6}\,m\]
(d) \[5\sqrt{6}\,m\]
(e) None of these
Answer: (b)
Exploration:
Let the height of the room be \[6x\] and its semi-perimeter be \[10x\].
Area of the four wall \[=2\times 6x\times 10x=120{{x}^{2}}\]
Area of the paper needed \[=120{{x}^{2}}-40\]
Length of the paper needed \[=\frac{120{{x}^{2}}-40}{1}\]
Total cost of the paper,
\[\text{1}0\times \text{(12}0{{x}^{\text{2}}}-\text{4}0\text{)}=\text{17}00\]
\[\text{12}0{{x}^{\text{2}}}~=\text{ 21}0\]
\[{{x}^{\text{2}}}~=\frac{\text{21}0}{120}=1.75\]
\[x=\sqrt{1.75}\,m\]
Therefore, height of the room is \[6\sqrt{1.75}\,m\].
![]() A solid in the form of right circular cone mounted on a hemisphere having radius 3.5 cm and height of the conical part is 5 cm is immersed in a cylindrical bucket whose radius and height are 5 cm and 9.8 cm respectively containing water. When the solid is immersed in the bucket some of the water from the bucket spelt out. The volume of the water left in the bucket:
A solid in the form of right circular cone mounted on a hemisphere having radius 3.5 cm and height of the conical part is 5 cm is immersed in a cylindrical bucket whose radius and height are 5 cm and 9.8 cm respectively containing water. When the solid is immersed in the bucket some of the water from the bucket spelt out. The volume of the water left in the bucket:
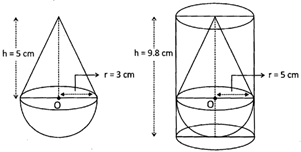
(a) \[\text{576 c}{{\text{m}}^{\text{3}}}\]
(b) \[\text{616 c}{{\text{m}}^{\text{3}}}\]
(c) \[\text{484 c}{{\text{m}}^{\text{3}}}\]
(d) \[\text{764 c}{{\text{m}}^{\text{3}}}\]
(e) None of these
Answer: (a)
![]() A metallic pillar is such that its lower part is in the form of cylinder mounted by a right circular cone. The radius of the pillar is 7 cm and the height of the cylindrical part is 250 cm and that of the conical part is 60 cm. If the density of the metallic pillar is 8 gm/cm cube, then find the weight of the pillar in kg.
A metallic pillar is such that its lower part is in the form of cylinder mounted by a right circular cone. The radius of the pillar is 7 cm and the height of the cylindrical part is 250 cm and that of the conical part is 60 cm. If the density of the metallic pillar is 8 gm/cm cube, then find the weight of the pillar in kg.
(a) 396.69kg
(b) 356.85kg
(c) 323.54kg
(d) 332.64kg
(e) None of these
Answer: (d)
![]() Mr. Robert purchased a toy for his son Michael. The toy is in the form of hemisphere at one end and in the form of cone at the other end and cylindrical in the middle. The radius and height of the cylindrical part are 5 cm and 13 cm respectively. The radii of hemispherical and conical part is same as that of cylindrical part. If the total length of the toy is 40 cm, then find its total surface area.
Mr. Robert purchased a toy for his son Michael. The toy is in the form of hemisphere at one end and in the form of cone at the other end and cylindrical in the middle. The radius and height of the cylindrical part are 5 cm and 13 cm respectively. The radii of hemispherical and conical part is same as that of cylindrical part. If the total length of the toy is 40 cm, then find its total surface area.
(a) \[\text{911}.\text{43c}{{\text{m}}^{\text{2}}}\]
(b) \[\text{895}.\text{5c}{{\text{m}}^{\text{2}}}\]
(c) \[\text{784}.\text{54}\,\text{c}{{\text{m}}^{\text{2}}}\]
(d) \[\text{1}0\text{22}.\text{56c}{{\text{m}}^{\text{2}}}\]
(e) None of these
Answer: (a)
![]() A letter 'T' shape is made by sticking together 2 cuboids as shown in the diagram. What is the total volume of the letter 'T'?
A letter 'T' shape is made by sticking together 2 cuboids as shown in the diagram. What is the total volume of the letter 'T'?
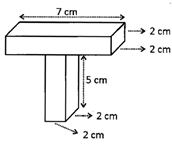
(a) \[\text{57c}{{\text{m}}^{\text{3}}}\]
(b) \[\text{64}\,\text{c}{{\text{m}}^{\text{3}}}\]
(c) \[\text{48c}{{\text{m}}^{\text{3}}}\]
(d) \[\text{25c}{{\text{m}}^{\text{3}}}\]
(e) None of these
Answer: (c)
Exploration:
Volume of upper part
\[\text{7}\times \text{2}\times \text{2}=\text{28c}{{\text{m}}^{\text{3}}}\]
Volume of lower part
\[\text{5}\times \text{2}\times \text{2}=\text{2}0\text{ c}{{\text{m}}^{\text{3}}}\]
Total volume\[~=\text{2}0+\text{28}=\text{48 c}{{\text{m}}^{\text{3}}}\]
Therefore, option (c) is correct and rest of the options is incorrect.
![]() A metallic spherical ball of radius 5 cm is dropped into a conical vessel containing water. The diameter of the vessel is 20 cm. If the ball is completely submersed in the vessel, the raise in water level in the vessel is:
A metallic spherical ball of radius 5 cm is dropped into a conical vessel containing water. The diameter of the vessel is 20 cm. If the ball is completely submersed in the vessel, the raise in water level in the vessel is:
(a) 5cm
(b) 4cm
(c) 6cm
(d) 3cm
(e) None of these
Answer: (a)
![]() Robert wants to water his garden with the pipe connected with a tank. If the water is flowing at the rate of 20 km/h through the pipe whose diameter is 15 cm. If the length and breath of the rectangular garden is 50 m and 45 m respectively, then find the time required to raise the level of the water by 20 cm in the garden?
Robert wants to water his garden with the pipe connected with a tank. If the water is flowing at the rate of 20 km/h through the pipe whose diameter is 15 cm. If the length and breath of the rectangular garden is 50 m and 45 m respectively, then find the time required to raise the level of the water by 20 cm in the garden?
(a) 345.45 sec
(b) 343.63 sec
(c) 350 sec
(d) 505.46cm
(e) None of these
Answer: (b)
![]() An open plastic bucket mounted on a cylindrical base is such that the diameters of the two ends are 48 cm and 28 cm. If the total height of the bucket is 35 cm and that of the cylindrical part is 5 cm, then find the area of the sheet require to make the bucket?
An open plastic bucket mounted on a cylindrical base is such that the diameters of the two ends are 48 cm and 28 cm. If the total height of the bucket is 35 cm and that of the cylindrical part is 5 cm, then find the area of the sheet require to make the bucket?
(a) \[\text{4832}.\text{33c}{{\text{m}}^{\text{2}}}\]
(b) \[\text{3822}.\text{5c}{{\text{m}}^{\text{2}}}\]
(c) \[\text{3587}\text{.33c}{{\text{m}}^{\text{2}}}\]
(d) \[\text{4589}.\text{69}\,\text{c}{{\text{m}}^{\text{2}}}\]
(e) None of these
Answer: (a)
![]() Martina is a national badminton player and also a national champion in badminton. She uses a shuttlecock such that the diameters of the two ends are 8 cm and 4 cm respectively and the height of the entire shuttlecock is 8 cm. It is mounted with a hemispherical shaped at the lower end. Find the external surface area of the shuttlecock.
Martina is a national badminton player and also a national champion in badminton. She uses a shuttlecock such that the diameters of the two ends are 8 cm and 4 cm respectively and the height of the entire shuttlecock is 8 cm. It is mounted with a hemispherical shaped at the lower end. Find the external surface area of the shuttlecock.
(a) 176.84cm2
(b) \[\text{156}.\text{46}\,\text{c}{{\text{m}}^{\text{2}}}\]
(c) \[\text{144}.\text{32}\,\text{c}{{\text{m}}^{\text{2}}}\]
(d) \[\text{114}.\text{96c}{{\text{m}}^{\text{2}}}\]
(e) None of these
Answer: (c)
![]() The dimension of the James guest room is \[\text{14m}\times \text{12m}\times \text{1}0\text{m}\]. He wants to fix a pole in his room so that he can hang some of the important posters on it. He wants that the room should contain maximum number of the posters on it. The length of the longest pole he can fit in his room is:
The dimension of the James guest room is \[\text{14m}\times \text{12m}\times \text{1}0\text{m}\]. He wants to fix a pole in his room so that he can hang some of the important posters on it. He wants that the room should contain maximum number of the posters on it. The length of the longest pole he can fit in his room is:
(a) 21.36m
(b) 20.44m
(c) 22.56m
(d) 20.98m
(e) None of these
Answer: (d)
You need to login to perform this action.
You will be redirected in
3 sec
