Direction Sense
Category : 8th Class
Introduction
Direction sense is an ability to know roughly where you are, or which way to go, even when you are in an unfamiliar place.
DIRECTION SENSE TEST:
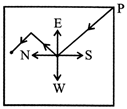
There are four directions North, South, East and West. The word
NEWS came from North, East, West and South. There are four regions:
North-East (I); South-East (IV); North-West (II); South-West (III).
The directions OP, OS, OQ and OR are North East direction; North West direction; South-West and South-East direction.
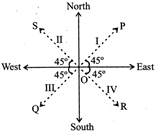
The candidate must distinguish between the regions and directions i.e. between North-East region and North-East direction.
If you move with your face east-wards, your left hand is towards north and your right hand is towards south. Similarly the positions of the directions of the hands can be fixed when you move in any of the other three directions.
To solve the question, first draw the direction figure
 on paper. Mark the starting point. After that move carefully according to the directions given in the question.
on paper. Mark the starting point. After that move carefully according to the directions given in the question.
EXAMPLE 1:
Distance between e and g is:
(a) 2 km (b) 1 km
(c) 5 km (d) 1.5 km
EXAMPLE 2:
Distance between a and f is:
(a) 1.41 km (b) 3 km
(c) 2 km (d) 1 km
EXAMPLE 3:
Distance between e and i is:
(a) 4 km (b) 2 km
(c) 1 km (d) 3 km
Sol. (1-3):
From the information given, positions of houses are as follows:
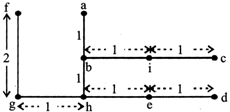
Sol. 1: (a)
Clearly, the distance between e and g is 2 km.
Sol. 2: (d)
From the above diagram, the distance between a and f is 1 km.
Sol.3: (c)
Clearly, the distance between e and i is 1km.
EXAMPLE 4:
In the given figure, P is 300 km eastward of O and Q is 400 kms North of O, R is exactly in the middle of Q and P. The distance between Q and R is :
(a) 250kms (b) \[250\sqrt{2}\] kms
(c) 300 kms (d) 350 kms
(e) None of these
Sol. (a) \[PQ=\sqrt{O{{P}^{2}}+O{{Q}^{2}}}\]
\[=\sqrt{{{(300)}^{2}}+{{(400)}^{2}}}=\sqrt{{{100}^{2}}({{3}^{2}}+{{4}^{2}})}\]
\[=\sqrt{{{100}^{2}}\times {{5}^{2}}}=(100\times 5)\] i.e., \[500km\]
R being in the midway of PQ, so QR= 250 kms.
EXAMPLE 5:
Four persons stationed at the four comers of a square piece as shown in the diagram. P starts crossing the field diagonally. After walking half the distance, he turns right, walks some distance and turns left.
Which direction is P facing now?
(a) North-east (b) North-west
(c) North (d) South-east
(e) South-west
Sol. (b)
The route of P is shown in the diagram.
Clearly the direction of P is North-west.
Miscellaneous Solved Examples
EXAMPLE 1:
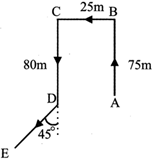
Deepa moved a distance of 75 meters towards the north. She then turned to the left turned to the right at an angle of \[{{45}^{o}}\]. In which direction was she moving finally?
(a) North-east (b) North-west
(c) South (d) South-east
Sol. (d) Deepa started from A, moved 75m upto B turned left and walked 25 m upto C. She then Turning to the right at an angle of \[{{45}^{o}}\], she was finally moving in the direction DE i.e., south west.
EXAMPLE 2:
Johnson left for his office in his car. He drove 15 km towards north and then 10 km towards west. He then turned to the south and covered 5 km. Further, he turned to the east and moved 8 km. Finally, he turned right and drove 10 km. How far and in which direction is he from his starting point?
(a) 2 km west (b) 5 km East
(c) 3 km north (d) 6 Km south
Sol. (a) Clearly, Johnson drove 15 km from A to B north wards and then 10 km from B to C towards west. He then moves 5 km southwards from C to D and 8 km eastwards upto E. Finally, he turned right and moved 10 km upto F.
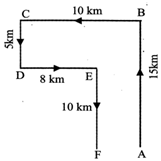
\[\therefore \] A and F lie in the same straight line and F lies to the west of A.
So, Johnson's distance from the starting point
A = AF= (BC-DE) = (10-8) km=2km.
EXAMPLE 3:
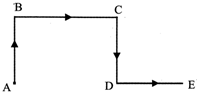
You go North, turn right, then right again and then go to the left. In which direction are you now?
(a) North (b) South
(c) East (d) West
Sol. (c) The movements indicated are as shown in fig. (A to B, B to C. C to D and D to E). Clearly, E lies to the east of
EXAMPLE 4:
A man leaves for his office from his house. He walks to-wards east. After moving a distance of 20 m, he turns south and walks 10m. Then he walks 35 m towards the west and further 5 m towards the North. He then turns towards east and walks 15m. What is the straight distance (in metres) between his initial and final positions?
(a) 0 (b) 5
(c) 10 (d) Cannot be determined
Sol. (b) The movements of the man from A to Fare as shown in fig
Clearly \[DC=AB+EF.\]
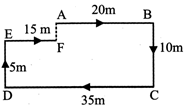
\[\therefore \] F is in line with A.
Also, AF=(BC-DE)=5m.
EXAMPLE 5:
So, the man is 5 metres away from his initial position. A person starts from a point A and travels 3 km eastwards to, B and then turns left and travels thrice that distance to reach C. He again turns left and travels five times the distance he covered between A and B and reaches his destination D. The shortest distance between the starting point and the destination is
(a) 12 km (b) 15 km
(c) 16 km (d) 18 km
Sol. (b) The movement of the person are as shown fig.
Clearly, AB= 3 km,
\[BC=3AB=(3\times 3)km=9km\]
\[CD=5AB=(5\times 3)km=15km\]
Draw \[AE\bot CD\].
Then \[CE=AB=3\] km and
\[AE=BC=9km\]
\[DE=(CD-CE)=(15-3)km=12km.\]
In \[\Delta AED,A{{D}^{2}}=A{{E}^{2}}+D{{E}^{2}}\]
\[\Rightarrow \]\[AD=(\sqrt{{{9}^{2}}+{{(12)}^{2}}})km=\sqrt{225}km=15km.\]
\[\therefore \] Required distance = AD = 15 km.
EXAMPLE 6:
Lokesh’s school bus is facing north when it reaches his school. After starting from Lokesh's house, it turns right twice and then left before reaching the school. What direction was the bus facing when it left the bus stop in front of Lokesh's house?
(a) North (b) South
(c) East (d) West
Sol. (d)
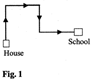
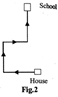
In fig 1, the route of the bus from Lokesh's house to the school is shown. It is given that the bus faces North on reaching the school. Now turning fig. 1 \[{{90}^{o}}\] anti-clockwise. We obtain fig. 2 which satisfies the specified conditions. It is evident from fig. 2 that the bus faces west in front of Lokesh's house.
EXAMPLE 7:
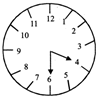
A watch reads 4.30 If the minute hand points East, in what direction will the hour hand point?
(a) North (b) North-west
(c) South-east (d) North-east
Sol. (d)
EXAMPLE 8:
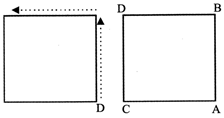
From the positions in original figure, C and A move diagonally to opposite comers and then one side each clockwise and anti-clockwise respectively. B and D move two sides each clockwise and anti-clockwise respectively. Where is A now?
(a) At the south-west comer
(b) At the north-east comer
(c) At the south east corner
(d) At the south-west corner
Sol. (d) The movements of A, C, B and D are shown in figures (i), (ii), (ill) and (iv) respectively. The final configuration is shown in (v). Comparing (v). with the given diagram A is in the south- west comer.
EXAMPLE 9:
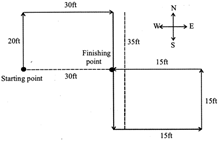
A child crawls 20 feet towards North, turns right and crawls 30 feet, turns right again and crawls 35 feet. He turns left again and crawls 15 feet. He turns left again and crawls 15 feet. Finally he turns to his left to crawl another 15 feet. How far is he from his starting point and in which direction
(a) 45 feet North-East (b) 30 feet East
(c) 30 feet West (d) 15 feet West
Sol. (b)
You need to login to perform this action.
You will be redirected in
3 sec
