Triangles
Category : 6th Class
A triangle has three sides and three vertices. The sum of the three angles of a triangle is equal to 180° and one angle of a triangle \[={{180}^{o}}-\] (Sum of two angles).
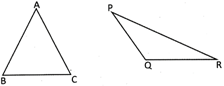
In ABC, \[\angle A+\angle B+\text{ }\angle C={{180}^{o}}\]
In APQR, \[\angle P+\angle Q+\angle R={{180}^{o}}\]
![]()
Find the measurement of A if B and C are given when A, B and C are the angles of the triangle.
(a) \[~A={{180}^{o}}-(B+C)\]
(b) \[A={{180}^{o}}+(B-C)\]
(c) \[A={{180}^{o}}+C-B\]
(d) All of these
(e) None of these
Answer: (a)
Explanation
The sum of angles of the triangle \[={{180}^{o}}.\]
Hence, the angle \[A={{180}^{o}}-(B+C).\]
![]() Exterior
Exterior
Angle of a Triangle The angle between the produced side and its adjacent side of triangle is called exterior angle. The exterior angle is equal to the sum of two opposite interior angles of that triangle. In the picture given below the angles \[\angle ABD\] and \[\angle ACE\] are the exterior angles of the triangle.
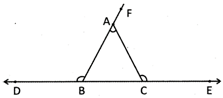
Thus,
\[\angle ACE=\angle BAC+\angle ABC\]
\[\angle ABD=\angle BAC+\angle ACB\]
\[\angle CAF=\angle ABC\text{ }+\angle ACB\]
![]()
Find the measurement of the angles x and y from the picture given below.
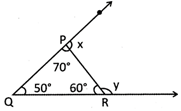
(a) \[x={{80}^{o}}\]and\[y={{10}^{o}}\]
(b) \[x={{110}^{o}}\]and\[~y={{120}^{o}}\]
(c) \[x={{70}^{o}}\]and\[y={{90}^{o}}\]
(d) All of these
(e) None of these
Answer: (b)
Explanation
\[x\]and\[y\] are the exterior angle therefore,
\[x=\angle PRQ\text{ }+\angle PQR={{60}^{o}}+{{50}^{o}}={{110}^{o}}\]
\[y=\angle QPR+\angle PQR={{70}^{o}}+{{50}^{o}}={{120}^{o}}\]
![]() Area of the Triangle
Area of the Triangle
The area of a triangle is the area bounded by the sides of the triangle.
Heron's Formula To find the area of a triangle by Heron's Formula, First find the semi perimeter of a triangle by the following formula: \[s=\frac{a+b+c}{2}\] (Here "s" stands for half of perimeter or semi perimeter and a, b and c refers to 3 sides of the triangle) \[Area=\sqrt{s(s-a)(s-b)(s-c)}\]by heron's formulae.
![]()
If the sides of a triangle are 18 cm, 24 cm and 30 cm then find the area of the triangle.
(a) \[216c{{m}^{2}}\]
(b) \[210c{{m}^{2}}\]
(c) \[21c{{m}^{2}}\]
(d) All of these
(e) None of these
Answer: (a)
Explanation
Let sides A = 18 cm, B = 24 cm, C = 30 cm \[s=\frac{a+b+c}{2}=\frac{18+24+30}{2}=\frac{72}{2}=36\] \[Area=\sqrt{s(s-a)(s-b)(s-c)}\]by heron's formulae \[=\sqrt{36\left( 36-18 \right)\left( 36-24 \right)\left( 36-30 \right)}\] \[=\sqrt{36\times 18\times 12\times 6}\] \[=\sqrt{{{6}^{2}}\times 9\times 2\times 6\times 2\times 6}\] \[=\sqrt{{{6}^{2}}\times {{3}^{2}}\times {{2}^{2}}\times {{6}^{2}}}\] \[=\sqrt{{{(6\times 3\times 2\times 6)}^{2}}}=6\times 3\times 2\times 6=216\,c{{m}^{2}}\]
Area of the Right Angled
Triangle The area of a right angle triangle is the half of the Product of height and base. Therefore the area of a right angle triangle \[\text{=}\frac{\text{1}}{\text{2}}\text{ }\!\!\times\!\!\text{ base }\!\!\times\!\!\text{ height}\text{.}\]
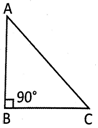
In the figure above AB is the height or altitude of the triangle ABC, AC is the hypotenuse and BC is the base of the triangle. The angle ABC is \[{{90}^{o}}.\] Therefore triangle ABC is called a right angled triangle.
![]()
If the base of a triangle is 18 cm and distance between base and opposite vertex is 10 cm, what will be the area of triangle?
(a) \[206c{{m}^{2}}~\]
(b) \[10c{{m}^{2}}\]
(c) \[90c{{m}^{2}}\]
(d) All of these
(e) None of these
Answer: (c)
Explanation
The distance between base and opposite vertex is height. The area \[=\frac{1}{2}\times base\text{ }\times distance\]of base from its opposite vertex (height attitude)
\[=\frac{1}{2}\times 18\times 10=90\,c{{m}^{2}}\]
Area of the Equilateral Triangle All three sides of the equilateral triangle are equal. Therefore the area of an equilateral triangle \[=\frac{\sqrt{3}}{4}\times {{(side)}^{2}}\]
![]()
Find the area of an equilateral triangle whose each side is 6 cm?
(a) \[9\sqrt{3}\,c{{m}^{2}}\]
(b) \[10\sqrt{2}\,c{{m}^{2}}\]
(c) \[90c{{m}^{2}}\]
(d) All of these
(e) None of these
Answer: (a)
Explanation
Area of an equilateral triangle \[=\frac{\sqrt{3}}{4}\times {{(side)}^{2}}=\frac{\sqrt{3}}{4}\times {{6}^{2}}=\frac{\sqrt{3}}{4}\times 36=9\sqrt{3}\,c{{m}^{2}}\]

![]()
You need to login to perform this action.
You will be redirected in
3 sec
