Perimeter and Area of Plane Figures
Category : 9th Class
Perimeter of every figure is sum of its sides. The perimetre of a rectangular room is the sum of measurement of all sides where the area of a rectangle is the product of their sides. Therefore, the sum of the length of all the sides of a geometrical shape is called perimetre. Sl unit for measurement of perimetre is meter and Sl unit of area is square metre.
![]() Perimeter and Area of Triangles
Perimeter and Area of Triangles
A triangle is one of the basic shapes of geometry. It has three vertices and three sides. Perimetre of triangle = Sum of the length of sides. Area of right angle triangle \[~=\frac{1}{2}\times Base\times Height\]
1. In the picture given below, ABC is a triangle whose sides are, AB, BC and AC. A perpendicular line AD is the height or altitude of the triangle. A square box at point D denotes the angle of \[{{90}^{o}}.\]
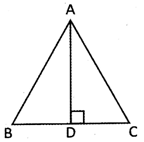
Perimeter of \[=AB+BC+CA.\]of its sides \[=AB+BC+CA.\] Area of \[\Delta ABC\,=\,\frac{1}{2}\times BC\times AD\] whereas BC is the base of the triangle and AD altitude.
![]()
Find the area and perimetre of the figure given below?
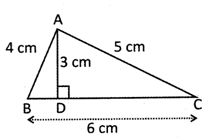
(a) \[8\text{ }c{{m}^{2}},15\text{ }cm\]
(b) \[~9\text{ }c{{m}^{2}},15\text{ }cm\]
(c) \[10\text{ }c{{m}^{2}},\text{ }8\text{ }cm\]
(d) All of these
(e) None of these
Answer: (b)
Explanation
Perimeter of \[\Delta ABC\]= Sum of its sides = AB + BC + CA= 4 cm + 6 cm + 5 cm = 15 cm Therefore, perimeter of \[\Delta ABC\text{ }=\text{ }15\text{ }cm\] Area of \[\Delta ABC=\frac{1}{2}BC\times AD\]whereas BC is the base of the triangle and AD is altitude. \[~\Delta ABC\text{ }=\text{ }9\text{ }c{{m}^{2}}\] The area of\[~\Delta ABC\text{ }=\text{ }9\text{ }c{{m}^{2}}\]
2. In the picture given below, a triangle has three equal sides, AB = BC = CA = a unit. Therefore, the triangle ABC is called equilateral triangle.
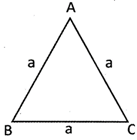
Perimeter of an equilateral triangle = AB + BC + CA \[=\text{ }Side\text{ }+\text{ }Side\text{ }+\text{ }Side\text{ }=\text{ }3\text{ }\times \text{ }Side\]
Therefore the perimetre of an equilateral triangle \[=3\times Side=\text{3}\times a\] Area of an equilateral triangle \[=\frac{\sqrt{3}}{4}\times {{(side)}^{2}}=\frac{\sqrt{3}}{4}\times {{a}^{2}}\]
![]()
Find the area of an equilateral triangle whose each side is 6 cm long?
(a) \[6\sqrt{3}\,\,c{{m}^{2}}\]
(b) \[8\sqrt{3}\,\,c{{m}^{2}}\]
(c) \[9\sqrt{3}\,\,c{{m}^{2}}\]
(d) All of these
(e) None of these
Answer: (c)
Explanation
The length of each side of the triangle is 6 cm therefore, it will be the equilateral triangle. Hence the area of the equilateral triangle =
\[\frac{\sqrt{3}}{4}\times {{(side)}^{2}}=\frac{\sqrt{3}}{4}\times 6\times 69\sqrt{3}\,\,c{{m}^{2}}.\]
![]() Perimeter and Area of Parallelogram
Perimeter and Area of Parallelogram
Parallelogram is a quadrilateral whose opposite sides are equal and parallel to each other.
Perimetre of Parallelogram = 2(sum of two adjacent sides)
Therefore, perimetre of parallelogram ABCD = 2(AB + BC)
= 2(3 cm + 4 cm)
= 14 cm
Area of a Parallelogram \[=\text{ }Base\times Height\]
Therefore, the area of a parallelogram \[ABCD=AB\times CE\]\[=3\text{ }cm\times 3.5\text{ }cm=10.5\text{ }c{{m}^{2}}\]
![]()
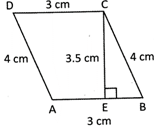
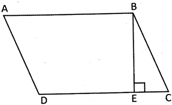
Find the area and perimetre of the parallelogram whose sides and altitude are AB = DC = 3 cm, AD = BC = 5 cm and BE = 4cm?
(a) \[7\text{ }c{{m}^{2}},16\text{ }cm\]
(b) \[8c{{m}^{2}},17cm\]
(c) \[12\text{ }c{{m}^{2}},16\text{ }cm\]
(d) All of these
(e) None of these
Answer: (c)
Explanation
Perimetre of \[\left\| \text{ABCD=2}\left( \text{Sum of adjacent sides} \right)\text{=2}\left( \text{3+5} \right)\text{=16 cm}\text{.} \right.\] Area of\[\left\| \text{ABCD=Base }\!\!\times\!\!\text{ Height=DC }\!\!\times\!\!\text{ BE=3 }\!\!\times\!\!\text{ 4=12 c}{{\text{m}}^{\text{2}}} \right.\]
![]() Perimeter and Area of Rectangle
Perimeter and Area of Rectangle
Rectangle has four right angles and equal opposite sides. Longer side of a rectangle is called length and shorter side is called width.
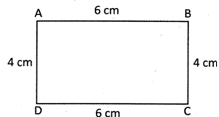
Perimetre of rectangle = AB + BC + CD + DA = length + width + length + width = 2 length + 2 width = 2 (length + width) Therefore,
(i) Perimetre of rectangle = 2 (length + width)
(ii) Area of rectangle = Length x Width
Area of rectangle \[ABCD\text{ }=\text{ }AB\text{ }\times \text{ }BC\] \[=6\text{ }cm\times 4\text{ }cm=24\text{ }c{{m}^{2}}\] Area of rectangle \[ABCD=24\text{ }c{{m}^{2}}\]
![]()
Through a rectangular field of dimensions 90 m and 60 m, two roads are constructed which are parallel to the sides of the rectangular field and cross each other at right angles at the centre of the field. If width of each road is 3 m. Find the area covered by the roads in the park.
(a) \[471{{m}^{2}}\]
(b) \[495{{m}^{2}}\]
(c) \[244{{m}^{2}}\]
(d) All of these
(e) None of these
Answer: (a)
Explanation
The area covered by path in the park =
\[2\left( 28.50\times 3 \right)+32+2\left( 48.50\times 3 \right)=171+9+291=471{{m}^{2}}\]Perimeter and Area of Rhombus A rhombus is a parallelogram with four equal sides. Therefore, perimeter of rhombus \[=4\times side.\]In the picture given below the length of sides of the rhombus is given.
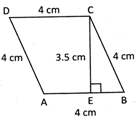
(i) Perimeter of rhombus,\[=4\times side\] Perimetre of rhombus, \[ABCD=4\times 4\text{ }cm=16\text{ }cm\] Perimetre of rhombus ABCD = 16 cm
(ii) Area of rhombus \[=\text{ }base\times height\] Area of rhombus \[ABCD=AB\times CE\] \[=\text{ }4\text{ }cm\text{ }\times 3.5\text{ }cm\] \[14\,\,c{{m}^{2}}\] Area of rhombus \[ABCD=14\text{ }c{{m}^{2}}\]
Note: Area of a rhombus when length of diagonals is given \[=\frac{1}{2}\times \]Product of length of diagonals
![]()
Find the area and perimetre of the picture given below, if PQ = QR = RS = SP = 15 cm and QM = 10 cm.
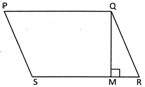
(a) \[149\text{ }c{{m}^{2}},\text{ }50\text{ }cm\]
(b) \[150\text{ }c{{m}^{2}},60\text{ }cm\]
(c) 244 cm2, 45 cm
(d) All of these
(e) None of these
Answer: (b)
Explanation
Area of PQRS = \[\text{15}\times \text{1}0=\text{15}0~\text{ c}{{\text{m}}^{\text{2}}}\]
Perimeter of \[PQRS=4\times side=4\times 15=60\text{ }cm.\]
![]() Perimetre and Area of Square
Perimetre and Area of Square
A square has four equal sides and each angle of \[{{90}^{o}}.\] In the picture given below, ABCD is a square because its all sides are equal and each angle is a right angle.
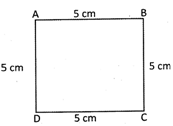
Perimetre of square ABCD = AB + BC + CD + DA Since all sides are equal, therefore, Perimetre of square = side + side + side + side \[=4\times \]side Area of Square\[~=side\times side={{\text{(}side\text{)}}^{2}}\] Area of Square\[~ABCD={{(5\text{ }cm)}^{2}}\] \[=25\text{ }c{{m}^{2}}\] Area of Square \[ABCD\text{ }=\text{ }25\text{ }c{{m}^{2}}\]
![]()
Find the area and perimetre in square metre and metre respectively of a square whose side is 600 cm.
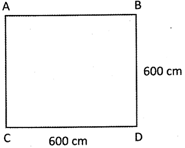
(a) \[36{{m}^{2}},\text{ }24m~\]
(b) \[15\text{ }{{m}^{2}},\text{ }6\text{ }m\]
(c) \[44{{m}^{2}},\text{ }5m\]
(d) All of these
(e) None of these
Answer: (a)
Explanation
Area of a square \[~ABCD={{\text{(}600\text{)}}^{2}}\text{ }=360000\text{ }c{{m}^{2}}.\] Perimetre of a square \[ABCD=4\times 600\text{ }2400\text{ }cm=24\text{ }m.\]
![]() Perimeter and Area of Trapezium
Perimeter and Area of Trapezium
A quadrilateral whose two sides are parallel and other two sides are non-parallel is called trapezium. The following figure is a trapezium.
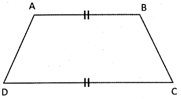
Parallel sides = AB and CD Non parallel sides = AD and BC
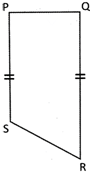
Parallel sides = PS and QR Non parallel sides = PQ and SR
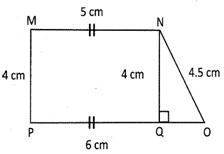
Parallel sides = MN and OP Non parallel sides = MP and ON Area of trapezium\[=\frac{1}{2}\times \] (Sum of parallel sides) \[\times \] distance between parallel side. Therefore the area of trapezium \[MNOP\text{ }=\frac{1}{2}\times \left( MN+OP \right)\times NQ\]
\[=\frac{1}{2}\times \text{(}5\text{ }cm+6\text{ }cm\text{)}\times 4\text{ }cm=22\text{ }c{{m}^{2}}\]
Perimetre of trapezium = Sum of the length of all sides Perimetre of trapezium MNOP = MN + ON + OP + PM = 5 cm + 4.5 cm + 6 cm + 4 cm =19.5 cm
![]()
Find the perimeter and area of trapezium whose two parallel sides are 4 m and 6 m long while the length of non-parallel sides are 10 m and 12 m. The length between the parallel sides is 8 m as shown in the picture given below.

(a) \[40{{m}^{2}},\text{ }32m\]
(b) \[15{{m}^{2}},\text{ }6m\]
(c) \[44{{m}^{2}},\text{ }5m\]
(d) All of these
(e) None of these
Answer: (a)
Explanation
Area of trapezium \[ABCD\text{ }=\frac{1}{2}\times \](Sum of parallel sides) \[\times \] distance between parallel side\[=\frac{1}{2}\times \text{(}4+6\text{)}\times 8=40\text{ }{{m}^{2}}.\] Perimetre of trapezium = Sum of the length of all sides = 4m + 6m + 10 m 12m = 32m.
![]() Circles
Circles
A round plane figure whose all points are equidistant from a fix point of its interior is called a circle.
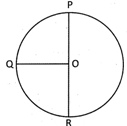
Point P, Q and R are equidistant from a fix point 0 that is at the interior region of the circle. The fix point from where all points of a circle are equidistant is called centre of the circle. The perimetre or boundary line of a circle is called circumference of the circle. The line which passes through the centre and join two points of the circumference is called diameter. Length of diameter is double of the length of its radius. Therefore, Diameter\[~=2\times \] Radius or d = 2r where d is diameter and r is radius.
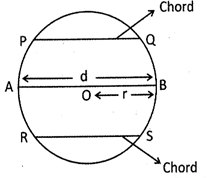
In the given figure, OB is radius and AB is diametre. A line segment which joins two points of circumference of a circle is called chord of the circle. In the figure given above PQ and RS are chord of the circle. Diametre is the longest chord of the circle. In the picture given below AB is the arc of the circle. Arc is a segment of circumference of the circle. Arc AB is denoted by \[\].

Relation between circumference and diameter: The ratio of circumference and diameter of a circle is always a constant denoted by \[\pi \].
\[\frac{Circumference}{Diametre}=Constant\] \[\frac{Circumference}{Diametre}=\pi \] \[\frac{Circumference2}{2r}=\pi \] Circumference or perimetre of a circle \[=2\pi r=\pi d.\] Area of circle \[=\pi {{r}^{2}}=\frac{\pi d}{4},\] where r = radius and d = diametre Area of semicircle \[\frac{\pi {{r}^{2}}}{2}=\frac{\pi {{d}^{2}}}{8}\]
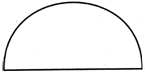
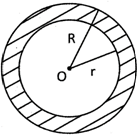
Perimeter of semicircle \[=\frac{2\pi r}{2}=\frac{\pi {{d}^{2}}}{8}\] \[=\pi r+2ra\] \[=r(\pi +2)\] Area of circular ring = Area of outer circle -Area of inner circle \[=\pi {{R}^{2}}+\pi {{r}^{2}}\]
\[=\pi ({{R}^{2}}-{{r}^{2}})\] Area of circular ring \[=\pi (R+r)(R-r)\]
![]()
Find the circumference of a circle whose diameter is 11.2 dm.
(a) 32dm
(b) 6dm
(c) 35.2dm
(d) All of these
(e) None of these
Answer: (c)
Explanation
d = 11.2 dm is given therefore the circumference \[=\pi d\]
\[=\frac{22}{7}\times 11.2=22\times 1.6=35.2dm.\]
You need to login to perform this action.
You will be redirected in
3 sec
