Trigonometric Functions
Category : 10th Class
In previous classes we have studied about the trigonometric ratio's in which we have studied about the various ratios of the sides of the triangle. In this chapter we will extend our studies till the relation between the various trigonometric ratios which is called trigonometric function and we will measure the angles in terms of radians.
![]() Sign of Trigonometric Function in Different Quadrants
Sign of Trigonometric Function in Different Quadrants
| FUNTION | 1st | 2nd | 3rd | 4th |
| \[\sin \,\theta \] | + | + | - | - |
| \[\cos \,\theta \] | + | - | - | + |
| \[\tan \,\theta \] | + | - | + | - |
| \[\cos ec\,\theta \] | + | + | - | - |
| \[sec\,\theta \] | + | - | - | + |
| \[\cot \,\theta \] | + | + | - | - |
Domain and Range of Trigonometric Function
| FUNCTION | DOMAIN | RANGE |
| \[1.\,Sin\theta \] | R | \[\left[ -1,\,1 \right]\] |
| \[2.\,Cos\theta \] | R | \[\left[ -1,\,1 \right]\] |
| \[3.\,Tan\theta \] | \[R-\left\{ 0,\frac{\pi }{2},\frac{3\pi }{2},\frac{5\pi }{2},--- \right\}\] | \[(-\propto ,\propto )\] |
| \[4.Co\sec \theta \] | \[R-\left\{ o,\pi 2\pi ,3\pi ,--- \right\}\] | \[(-\propto ,-1][1,\propto )\] |
| \[5.Sec\theta \] | \[R-\left\{ o,\frac{\pi }{2},\frac{3\pi }{2},\frac{5\pi }{2},--- \right\}\] | \[(-\propto ,-1][1,\propto )\] |
| \[6.Cot\theta \] | \[R-\{0,\pi ,2\pi ,3\pi ,---\}\] | \[(-\propto ,\propto )\] |
Graphical Representation of 5m, Cos and Tan Function
1. \[Sin\theta \]
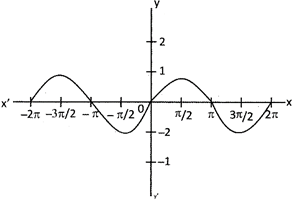
2. \[Cos\theta \]
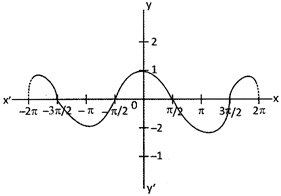
Conversion of Trigonometric Function of Complementary and Supple- mentary Angles
(A) \[\theta =\left( \frac{\pi }{2}-\theta \right)\]
1. \[Sin\left( \frac{\pi }{2}-\theta \right)=\cos \theta \]
2. \[Cos\left( \frac{\pi }{2}-\theta \right)=\sin \theta \]
3. \[Tan\left( \frac{\pi }{2}-\theta \right)=Cot\theta \]
4. \[Cot\left( \frac{\pi }{2}-\theta \right)=Tan\theta \]
5. \[Sec\left( \frac{\pi }{2}-\theta \right)=Co\sec \theta \]
6. \[Co\sec \left( \frac{\pi }{2}+\theta \right)=\sec \theta \]
(B) \[\theta =\left( \frac{\pi }{2}+\theta \right)\]
1. \[Sin\left( \frac{\pi }{2}+\theta \right)=Cos\theta \]
2. \[Cos\left( \frac{\pi }{2}+\theta \right)=-Sin\theta \]
2. \[Tan\left( \frac{\pi }{2}+\theta \right)=-Cot\theta \]
4. \[Tan\left( \frac{\pi }{2}+\theta \right)=-Cot\theta \]
3. \[Sec\left( \frac{\pi }{2}+\theta \right)=-Co\sec \theta \]
5. \[Co\sec =\sec \theta \]
(C) \[\theta =\left( \pi -\theta \right)\]
1. \[Sin\,(\pi -\theta )=\sin \theta \]
2. \[Cos\,(\pi -\theta )=-Cos\theta \]
3. \[Tan\,(\pi -\theta )=-Tan\theta \]
4. \[Cot\,(\pi -\theta )=-Cot\theta \]
5. \[Sec\,(\pi -\theta )=-\sec \theta \]
6. \[Cosec\,(\pi -\theta )=-Co\sec \theta \]
(D) \[\theta =(\pi +\theta )\]
1. \[Sin\,(\pi +\theta )=-\sin \theta \]
2. \[Cos\,(\pi +\theta )=-Cos\theta \]
3. \[Tan\,(\pi +\theta )=-\tan \theta \]
4. \[Cot\,(\pi +\theta )=-\cot \theta \]
5. \[Sec\,(\pi +\theta )=-\sec \theta \]
6. \[Co\sec \,(\pi +\theta )=-Co\sec \theta \]
(E) \[\theta =\left( \frac{3\pi }{2}-\theta \right)\]
1. \[Sin=\left( \frac{3\pi }{2}-\theta \right)=-\cos \theta \]
2. \[Cos=\left( \frac{3\pi }{2}-\theta \right)=-\sin \theta \]
3. \[Tan=\left( \frac{3\pi }{2}-\theta \right)=\cot \theta \]
4. \[Cot=\left( \frac{3\pi }{2}-\theta \right)=\tan \theta \]
5. \[Sec=\left( \frac{3\pi }{2}-\theta \right)=-\cos ec\theta \]
6. \[Cosec=\left( \frac{3\pi }{2}-\theta \right)=-sec\theta \]
(F) \[\theta =\left( \frac{3\pi }{2}-\theta \right)\]
1. \[Sin=\left( \frac{3\pi }{2}+\theta \right)=-\cos \theta \]
2. \[Cos=\left( \frac{3\pi }{2}+\theta \right)=\sin \theta \]
3. \[Tan=\left( \frac{3\pi }{2}+\theta \right)=-\cot \theta \]
4. \[Cot=\left( \frac{3\pi }{2}+\theta \right)=-\tan \theta \]
5. \[Sec=\left( \frac{3\pi }{2}+\theta \right)=\cos ec\theta \]
6. \[Cosec=\left( \frac{3\pi }{2}+\theta \right)=-sec\theta \]
(G) \[\theta =(2\pi -\theta )\]
1. \[Sin(2\pi -\theta )=-\sin \theta \]
2. \[Cos(2\pi -\theta )=Cos\theta \]
3. \[Tan(2\pi -\theta )=-Tan\theta \]
4. \[Cot(2\pi -\theta )=-Cot\theta \]
5. \[Sec(2\pi -\theta )=Sec\theta \]
6. \[Cosec(2\pi -\theta )=Cosec\theta \]
![]() Trigonometric Functions of Sum and Difference of two Angles
Trigonometric Functions of Sum and Difference of two Angles
1. \[Sin(A+B)=SinA.\,CosB+CosA.\,SinB\]
2. \[Sin(A-B)=SinA.\,CosB-CosA.\,SinB\]
3. \[Cos(A+B)=CosA.\,CosB-SinA.\,SinB\]
4. \[Cos(A-B)=CosA.\,CosB-SinA.\,SinB\]
5. \[Tan(A+B)=\frac{TanA+TanB}{1-TanA.TanB}\]
6. \[Tan(A-B)=\frac{TanA-TanB}{1+TanA.TanB}\]
7. \[Cot(A-B)=\frac{CotA.CotB-1}{CotA+CotB}\]
8. \[Cot(A+B)=\frac{CotA.CotB+1}{CotA-CotB}\]
9. \[Sin2A=SinA.CosA=\frac{2TanA}{1+Ta{{n}^{2}}A}\]
10. \[Cos\,2A=Co{{s}^{2}}A-Si{{n}^{2}}A=2Co{{s}^{2}}A-1\]\[=1-2{{\sin }^{2}}A=\frac{1-Ta{{n}^{2}}A}{1+Ta{{n}^{2}}A}\]
11. \[Tan2A=\frac{2TanA}{1-Ta{{n}^{2A}}}\]
12. \[Sin3A=3SinA-4Si{{n}^{3}}A\]
13. \[Cos3A=4Co{{s}^{3}}A-3CosA\]
14. \[Tan3A=\frac{3TanA-Ta{{n}^{3}}A}{1-3Ta{{n}^{2}}A}\]
![]() Some More Relations on Functions
Some More Relations on Functions
(A) 1. \[SinA+SinB=2Sin\frac{A+B}{2}Cos\frac{A-B}{2}\]
2. \[SinA+SinB=2Sin\frac{A-B}{2}Cos\frac{A+B}{2}\]
3. \[CosA+CosB=2Cos\frac{A-B}{2}Cos\frac{A+B}{2}\]
4. \[CosA-CosB=-2\sin \frac{A-B}{2}Sin\frac{A+B}{2}\]
(B) 1. \[SinA.SinB=\frac{1}{2}[Cos(A-B)-Cos(A+B)]\]
2. \[CosA.CosB=\frac{1}{2}[Cos(A-B)+Cos(A+B)]\]
3. \[SinA.CosB=\frac{1}{2}[Sin(A-B)+Sin(A+B)]\]
(C) 1. \[Sin(-A)=-SinA\]
2. \[Cos(-A)=CosA\]
3. \[Tan(-A)=-TanA\]

![]() Find the value of \[f\left( \theta \right)=\frac{\sin 5\theta -2\sin 3\theta +\sin \theta }{\cos 5\theta -\cos \theta }\].
Find the value of \[f\left( \theta \right)=\frac{\sin 5\theta -2\sin 3\theta +\sin \theta }{\cos 5\theta -\cos \theta }\].
(a) \[Tan\theta \]
(b) \[Sec\theta \]
(c) \[Sin\theta \]
(d) \[Cos\theta \]
(e) None of these
Answer: (a)
Explanation
We have, \[f\left( \theta \right)=\frac{\sin 5\theta -2\sin 3\theta +\sin \theta }{\cos 5\theta -\cos \theta }\]
\[\Rightarrow \,\,\,\frac{2\sin 3\theta \cos 2\theta -2\sin 3\theta }{-2\sin 3\theta \sin 2\theta }\]
\[\Rightarrow \,\,\,\frac{1-\cos 2\theta }{\sin 2\theta }=Tan\theta \]
![]() The value of \[2{{\sin }^{2}}\frac{3\pi }{4}+2{{\cos }^{2}}\frac{\pi }{4}+2{{\sec }^{2}}\frac{\pi }{3}\] is given by:
The value of \[2{{\sin }^{2}}\frac{3\pi }{4}+2{{\cos }^{2}}\frac{\pi }{4}+2{{\sec }^{2}}\frac{\pi }{3}\] is given by:
(a) 1
(b) 5
(c) 10
(d) 8
(e) None of these
Answer: (c)
Explanation
We have, \[2{{\sin }^{2}}\frac{3\pi }{4}+2{{\cos }^{2}}\frac{\pi }{4}+2{{\sec }^{2}}\frac{\pi }{3}\]
\[=2{{\left( \frac{1}{\sqrt{2}} \right)}^{2}}+2{{\left( \frac{1}{\sqrt{2}} \right)}^{2}}+2{{\left( 2 \right)}^{2}}\]
= 10
![]() The value of \[32{{\cos }^{6}}\theta -48{{\cos }^{4}}\theta +18{{\cos }^{2}}\theta -1\] is
The value of \[32{{\cos }^{6}}\theta -48{{\cos }^{4}}\theta +18{{\cos }^{2}}\theta -1\] is
(a) \[Cot3\theta \]
(b) \[Cos6\theta \]
(c) \[\sin 4\theta \]
(d) \[Tan3\theta \]
(e) None of these
Answer: (b)
Explanation
We have,
\[32{{\cos }^{6}}\theta -48{{\cos }^{4}}\theta +18{{\cos }^{2}}\theta -1\]
\[=32{{\cos }^{6}}\theta -4-48{{\cos }^{4}}\theta +24{{\cos }^{2}}\theta -6{{\cos }^{2}}\theta +3\]
\[=4(8co{{s}^{6}}\theta -1-12{{\cos }^{4}}\theta +6{{\cos }^{2}}\theta )-6{{\cos }^{2}}\theta +3\]
\[=4{{\left( 2{{\cos }^{2}}\theta -1 \right)}^{3}}-3\left( 2{{\cos }^{2}}\theta -1 \right)\]
\[=4{{\cos }^{3}}2\theta -3\cos 2\theta \]
\[=Cos6\theta \].
![]() Find the value of \[Co{{s}^{2}}\theta +Co{{s}^{2}}\left( \theta +\frac{\pi }{3} \right)+Co{{s}^{2}}\left( \theta -\frac{\pi }{3} \right)\].
Find the value of \[Co{{s}^{2}}\theta +Co{{s}^{2}}\left( \theta +\frac{\pi }{3} \right)+Co{{s}^{2}}\left( \theta -\frac{\pi }{3} \right)\].
(a) 1
(b) \[-\frac{3}{2}\]
(c) \[\frac{3}{2}\]
(d) \[-\frac{1}{2}\]
(e) None of these
Answer: (c)
![]() Find the value of \[2Cos\frac{\pi }{13}Cos\frac{9\pi }{13}+Cos\frac{3\pi }{13}+Cos\frac{5\pi }{13}\].
Find the value of \[2Cos\frac{\pi }{13}Cos\frac{9\pi }{13}+Cos\frac{3\pi }{13}+Cos\frac{5\pi }{13}\].
(a) 1
(b) 0
(c) – 1
(d) \[-\frac{1}{2}\]
(e) None of these
Answer: (b)
![]() The general solution of \[2{{\cos }^{2}}\theta -3\sin \theta =0\] is given by:
The general solution of \[2{{\cos }^{2}}\theta -3\sin \theta =0\] is given by:
(a) \[n\pi +\frac{7\pi }{6}\]
(b) \[2n\pi -\frac{7\pi }{6}\]
(c) \[2n\pi +\frac{7\pi }{6}\]
(d) \[n\pi +{{\left( -1 \right)}^{n}}\frac{7\pi }{6}\]
(e) None of these
Answer: (d)
Explanation
We have, \[2{{\cos }^{2}}\theta -3Sin\theta =0\]
\[\Rightarrow \,\,2\left( 1-Si{{n}^{2}}\theta \right)-3Sin\theta =0\]
\[\Rightarrow \,\,\left( 2Sin\theta +1 \right)\left( \sin \theta -2 \right)=0\]
\[\Rightarrow \,\,\,\,\,\text{sin}\theta =-\frac{1}{2}\text{or}\,\sin \theta =2\]
But \[\sin \theta =2\] is not possible
Therefore \[Sin\theta =-\frac{1}{2}\]
\[\Rightarrow \,\,\,\theta =\frac{7\pi }{6}\]
Hence the general solution is \[n\pi +{{\left( -1 \right)}^{n}}\frac{7\pi }{6}\]
![]() If \[Tan\left( \frac{\pi }{4}+\theta \right)+Tan\left( \frac{\pi }{4}-\theta \right)=2\], then the general solution is given by:
If \[Tan\left( \frac{\pi }{4}+\theta \right)+Tan\left( \frac{\pi }{4}-\theta \right)=2\], then the general solution is given by:
(a) \[n\pi \]
(b) \[-n\pi \]
(c) \[-n\pi +\frac{\pi }{6}\]
(d) \[-n\pi -\frac{\pi }{6}\]
(e) None of these
Answer: (a)
Explanation
We have, \[Tan\left( \frac{\pi }{4}+\theta \right)+Tan\left( \frac{\pi }{4}-\theta \right)=2\]
\[\Rightarrow \,\,\frac{1+\tan \theta }{1-\tan \theta }+\frac{1-\tan \theta }{1+\tan \theta }=2\]
\[\Rightarrow \,\,\,\,\frac{{{\left( 1+\tan \theta \right)}^{2}}+{{\left( 1-\tan \theta \right)}^{2}}}{1-{{\tan }^{2}}\theta }=2\]
\[\Rightarrow \,\,\,\,1+{{\tan }^{2}}\theta =1-{{\tan }^{2}}\theta \]
\[\Rightarrow \,\,\,\tan \theta =0\]
\[\Rightarrow \,\,\,\theta =n\pi \]for all integer n
![]() Find the general solution of the equation\[Sin\theta -Sin4\theta +Sin6\theta =0\].
Find the general solution of the equation\[Sin\theta -Sin4\theta +Sin6\theta =0\].
(a) \[\left( n\pi ,\pm \frac{\pi }{6} \right)\]
(b) \[\left( 2n\pi ,\pm \frac{\pi }{6},\frac{\pi }{4} \right)\]
(c) \[\left( -n\pi ,+\frac{\pi }{6},\frac{\pi }{2} \right)\]
(d) \[\left( n\pi ,\pm \frac{\pi }{6},\frac{n\pi }{4} \right)\]
(e) None of these
Answer: (d)
Explanation
We have \[Sin2\theta -Sin4\theta +Sin6\theta =0\]
\[\Rightarrow \,\,\,Sin4\theta \left( 2\cos 2\theta -1 \right)=0\]
\[\Rightarrow \,\,\theta =\frac{n\pi }{4}\,and\,\theta =n\pi \pm \frac{\pi }{6}\]
![]() If \[Sin\alpha =Sin\beta \,\,and\,Cos\alpha =Cos\beta \], then which one of the following options is correct and satisfies the above equation.
If \[Sin\alpha =Sin\beta \,\,and\,Cos\alpha =Cos\beta \], then which one of the following options is correct and satisfies the above equation.
(a) \[\alpha =\beta \]
(b) \[\alpha =-\beta \]
(c) \[\alpha =-2\beta \]
(d) \[\alpha +\beta =\pi \]
(e) None of these
Answer: (a)
![]() If \[Cos\theta +\sqrt{s3}\sin \theta =2\,and\,\theta \in \left[ 0,2\pi \right]\], then the value of 9 is given by:
If \[Cos\theta +\sqrt{s3}\sin \theta =2\,and\,\theta \in \left[ 0,2\pi \right]\], then the value of 9 is given by:
(a) \[\pi \]
(b) \[2\pi \] s
(c) \[\frac{\pi }{3}\]
(d) \[\frac{2\pi }{3}\]
(e) None of these
Answer: (c)

![]()
(A) \[\theta =\left( \frac{\pi }{2}-\theta \right)\]
You need to login to perform this action.
You will be redirected in
3 sec
