Relations between Roots of Quadratic Equation
Category : 10th Class
If ![]() are the roots of the quadratic equation
are the roots of the quadratic equation![]() , then the relation between the roots of the quadratic equation is given by,
, then the relation between the roots of the quadratic equation is given by,
Sum of the roots ![]()
Product of the roots ![]()
![]() Formation of Quadratic Equations
Formation of Quadratic Equations
If ![]() are the roots of the quadratic equation, S denotes its sum and P denotes its product, then the quadratic equation is given by:
are the roots of the quadratic equation, S denotes its sum and P denotes its product, then the quadratic equation is given by:
![]()
![]() Graphical Representation of a Quadratic Equation
Graphical Representation of a Quadratic Equation
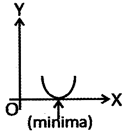
For the quadratic equation ![]() , the nature of graph for different values of D is: (a) If D < 0, and a > 0, then the graph is given by:
, the nature of graph for different values of D is: (a) If D < 0, and a > 0, then the graph is given by:
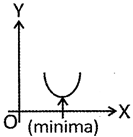
If a < 0, then the graph is given by.
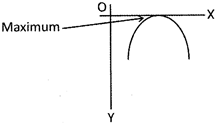
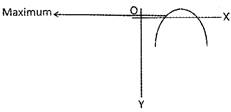
(b) If D = 0, and a > 0, then the graph of the function is given by
If a < 0, then the graph is given by
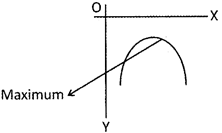
(d) If D > 0, and a > 0, then the graph of the function is given by,
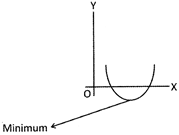
If a < 0, then the graph of the function is given by,
![]() Roots of Biquadratic Equation
Roots of Biquadratic Equation
Any biquadratic equation, ![]() , will have four roots. If a, P, Y, and 5 are its roots, then the relation between the roots is given by Sum of the roots
, will have four roots. If a, P, Y, and 5 are its roots, then the relation between the roots is given by Sum of the roots ![]()
Sum of product of two roots at a time ![]()
Sum of product of three roots at a time ![]()
Product of the roots ![]()

![]() Find the value of
Find the value of![]() .
.
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(e) None of these
Answer: (a)
Explanation
Let ![]()
![]()
![]()
![]()
![]()
![]() A If
A If ![]() are the roots of the equation
are the roots of the equation![]() , then the value of
, then the value of ![]() are.
are.
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(e) None of these
Answer: (b)
Explanation
We have, ![]()
![]()
![]() If
If ![]() is real and
is real and ![]() is the roots of
is the roots of ![]() , then find the value of
, then find the value of ![]() .
.
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(e) None of these
Answer: (d)
Explanation
We have sum of the roots ![]()
Product of the roots ![]()
Form the above two equations we get,
![]()
![]()
![]()
![]()
![]() If
If ![]() are the roots of
are the roots of ![]() and
and ![]() are the roots of
are the roots of![]() , then find the value of
, then find the value of ![]() .
.
(a) 15
(b) 33
(c) 41
(d) 63
(e) None of these
Answer: (b)
![]() If the coefficient of z in the quadratic equation
If the coefficient of z in the quadratic equation ![]() is taken as 18 in place of 12 and its roots were found to be -16 and -2. The roots of the original equation are:
is taken as 18 in place of 12 and its roots were found to be -16 and -2. The roots of the original equation are:
(a) - 12 & - 6
(b) - 14 & - 4
(c) - 16 & - 2
(d) ? 8 &- 4
(e) None of these
Answer: (d)

![]()
You need to login to perform this action.
You will be redirected in
3 sec
