10th Class Mathematics Polynomials Division of Polynomials

       Division of Polynomial

Previously we have studied about the division of the real numbers, in which we obtained quotient and remainders which satisfies the relation,

                Dividend = Quotient \[\times \] Divisor + Remainder

This is also known as Euclid's division lemma. In this section we will discuss about the division of the polynomials which is known as the division algorithm for polynomials. The concept of division of the polynomials can be used for finding the zeroes of the cubic or biquadratic polynomials.

Divide the polynomial \[g(x)={{x}^{3}}-3{{x}^{2}}+3{{x}^{2}}+3x-5\] by the polynomials \[h(x)={{x}^{2}}+x+1\] and find the quotient and remainder.

(a) \[(x-4,6x-1)\]                             

(b) \[(x+4,6x+1)\]

(c) \[({{x}^{2}}+1,3x+2)\]                             

(d) \[({{x}^{2}}+1,x-2)\]

(e) None of these

Answer: (a)

Explanation

When we divide \[g(x)\,by\,h(x)\] we have,

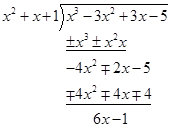
Find the remaining two zeroes of the polynomial \[h(y)=3{{y}^{4}}+6{{y}^{3}}-2y-10y\,5\] if the two zeroes of the polynomial is \[\pm \sqrt{\frac{5}{3}}\].

(a) (- 1, 1)                                           

(b) (-1, - 1)

(c) (+ 1, 2)                                           

(d) (- 2 , 2)

(e) None of these

Answer: (b)

Explanation

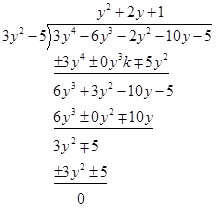
Find the value of m and n such that \[{{z}^{2}}+1\] is the factor of \[g(z)={{z}^{4}}+{{z}^{3}}+8{{z}^{2}}+mz+n.\].

(a) ( - 1, - 7)                                        

(b) ( - 1, - 1)

(c) (1, 2)                                              

(d) (1, 7)

(e) None of these

Answer: (d)

Find the value of k and p in the polynomial \[m(z)={{z}^{4}}-6{{z}^{3}}+16{{z}^{2}}-25z+10\] is divisible by\[n(z)={{z}^{2}}-2z+k\], gives the remainder z + p.

(a) \[(k=-5,p=-7)\]                          

(b) \[(k=-5,p=-1)\]

(c) \[(k=5,p=-5)\]                            

(d) \[(k=1,p=7)\]

(e) None of these

Answer: (c)

If the polynomial \[g(m)=6{{m}^{4}}+8{{m}^{3}}+17{{m}^{2}}+21m+7\] is divisible by another polynomial \[h(m)=3{{m}^{2}}+4m+1\] gives the remainder qm + a, then find the value of q and a.

(a) (q = 5, a = -7)                              

(b) (q = 1, a = 2)

(c) (q = 2, a = -5)                              

(d) (q = 1, a = -2)

(e) None of these

Answer: (b)

• The number of trees with 10 is the number 106.
• The smallest possible value of the longest edge in a Heronian Tetrahedron is the number 117.
• The smallest number to appear 6 times in Pascal's triangle is 120.
• The smallest number that is not of the form | 12x - 3y | is 41.
• 50 is the smallest number that can be written as the sum of 2 squares in 2 ways.

• For any polynomials \[p(x)={{a}_{0}}+{{a}_{1}}x+{{a}_{2}}{{x}^{2}}+----+{{a}_{n}}{{x}^{n}},x\] is a variable and \[{{a}_{0}},{{a}_{1}},{{a}_{2}},---{{a}_{n}}\] are constants.
• The highest power of the variable in the polynomial is called degree of the polynomial.
• A polynomial of degree zero is called constant polynomial.
• A real number 'a' is called zeroes of the polynomial if F (a) = 0.
• A polynomial of degree n will have n zeroes.