Graphical Representation
Category : 10th Class
(A) Consistent Equation
It has two types of solutions: unique or infinitely many solutions.
(1) Unique Solution
If the graph of the pair of linear equation is intersecting each other at one point, then the system is said to have unique solution. The point at which the two lines intersect each other is called solution of the system of equation.
\[4x-6y=-4,8x+2y=48\]
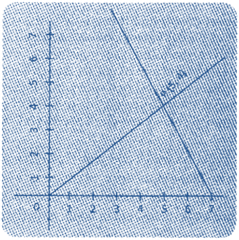
(2) Infinitely Many Solutions
If the graph of the pair of linear equation is coincident, then the system of linear equation is said to have infinitely many solutions.
\[y=3x+2\,and\,6x-2y+4=0\]
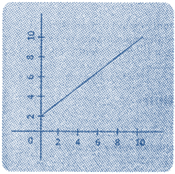
(B) Inconsistent Equation
It has only one type of solution, which is no solution.
(1) No Solution
If the graph of the system of equation is parallel and does not intersect each other at any point, then it is said to have no solution.
\[3x+3y=15\]
\[2y=-2x+6\]
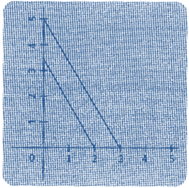
You need to login to perform this action.
You will be redirected in
3 sec
