Introduction
Category : 10th Class
Circle is defined as the locus of a point which is at a constant distance from a fixed point. The fixed point is called the centre of the circle and the fixed distance is called the radius of the circle.
A tangent to a circle is a line which intersects the circle at exactly one point. The point where the tangent intersects the circle is known as the point of contact.
![]() Properties of tangent to a circle
Properties of tangent to a circle
Following are some properties of tangent to a circle:
From the above points we conclude that in the following figure;
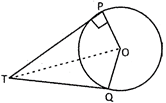
\[\angle OPT=\angle OQT={{90}^{o}},\,\angle POT=\angle QOT\] \[\angle QTO=\angle OTP\,and\,PT\,=\,QT\]
![]()
Two tangents PT and QT are drawn to a circle with centre 0 from an external point as shown in the following figure, then:
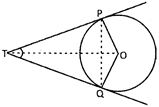
(a) \[\angle QTP=\angle QPO\]
(b) \[\angle QTP=2\angle QPO\]
(c) \[\angle QTP=3\angle QPO\]
(d) \[\angle QTP={{90}^{o}}\]
(e) None of these
Answer: (b)
Explanation
In the given figure, we have
TP = TO. [tangents drawn from an external point are equal in length]
\[\Rightarrow \,\,\angle TPQ=\,\angle TPQ\]
\[In\,\angle QTQ,\,we\,\,have\]
\[\angle TPQ+\angle TQP+PTQ={{180}^{o}}\]
\[\Rightarrow \,\angle TPQ={{90}^{o}}-\frac{1}{2}\angle PTQ\]
\[\Rightarrow \,\frac{1}{2}\angle PTQ={{90}^{o}}-\angle TPQ\] .... (i)
Also, \[\angle OPT={{90}^{o}}\]
\[\Rightarrow \,\angle OPQ={{90}^{o}}-\angle TPQ\] .... (ii)
From (i) and (ii), we get
\[\frac{1}{2}\angle PTQ=\angle OPQ\Rightarrow \angle PTQ=2\angle OPQ\]
You need to login to perform this action.
You will be redirected in
3 sec
