Let \[{{v}_{i}}\] be the instantaneous velocity of projectile at time t direction of this velocity is along the tangent to the trajectory at point P. \[{{\vec{v}}_{i}}={{v}_{x}}i+{{v}_{y}}\hat{j}\Rightarrow {{v}_{i}}=\sqrt{v_{x}^{2}+v_{y}^{2}}=\sqrt{{{u}^{2}}{{\cos }^{2}}\,\theta +{{(u\sin \theta -gt)}^{2}}}\] \[{{v}_{i}}=\sqrt{{{u}^{2}}+{{g}^{2}}{{t}^{2}}-2u\,gt\sin \theta }\] Direction of instantaneous velocity \[\tan \alpha \,=\,\frac{{{v}_{y}}}{{{v}_{x}}}=\frac{u\,\sin \,\theta -gt}{u\,\cos \theta }\] or \[\alpha ={{\tan }^{-1}}\left[ \tan \theta -\frac{gt}{u}\sec \theta \right]\] (4) Change in velocity: Initial velocity (at projection point) \[{{\overrightarrow{u}}_{i}}=u\cos \theta \,\hat{i}+u\sin \theta \,\hat{j}\] Final velocity (at highest point) \[{{\overrightarrow{u}}_{f}}=u\cos \theta \,\hat{i}+0\,\hat{j}\] (i) Change in velocity (Between projection point and highest point) \[\Delta u={{\overrightarrow{u}}_{f}}-{{\overrightarrow{u}}_{i}}=-u\sin \theta \,\hat{j}\] When body reaches the ground after completing its motion then final velocity \[{{\overrightarrow{u}}_{f}}=u\cos \theta \,\hat{i}-u\sin \theta \,\hat{j}\] (ii) Change in velocity (Between complete projectile motion) \[\Delta u={{u}_{f}}-{{u}_{i}}=-2u\sin \theta \,\hat{i}\] Sample problems based on velocity Problem 6. In a projectile motion, velocity at maximum height is [AIEEE 2002] (a) \[\frac{u\,\cos \,\theta }{2}\] (b) \[u\,\cos \,\theta \] (c) \[\frac{u\,\sin \,\theta }{2}\] (d) None of these Solution: (b) In a projectile motion at maximum height body possess only horizontal component of velocity i.e. u \[cos\,\theta \]. Problem 7. A body is thrown at angle 30o to the horizontal with the velocity of 30 m/s. After 1 sec, its velocity will be (in m/s) \[\left( g = 10 m/{{s}^{2}} \right)\] (a) \[10\sqrt{7}\] (b) \[700\sqrt{10}\] (c) \[100\sqrt{7}\] (d) \[\sqrt{40}\] Solution: (a) From the formula of instantaneous velocity \[v=\sqrt{{{u}^{2}}+{{g}^{2}}{{t}^{2}}-2\,u\,g\,t\,\sin \theta }\] \[v=\sqrt{{{(30)}^{2}}+{{(10)}^{2}}\times {{1}^{2}}-2\times 30\times 10\times 1\times \sin {{30}^{o}}}\] \[=10\sqrt{7}\,m/s\] Problem 8. A projectile is fired at \[{{30}^{o}}\] to the horizontal. The vertical component of its velocity is 80 ms?1. Its time of flight is T. What will be the velocity of the projectile at \[\operatorname{t} = T/2\] (a) \[80\text{ }m{{s}^{1}}\] (b) \[80\sqrt{3}\,m{{s}^{-1}}\] (c) \[(80/\sqrt{3})\,m{{s}^{-1}}\] (d) \[40\text{ }m{{s}^{1}}\] Solution: (b) At half of the time of flight, the position of the projectile will be at the highest point of the parabola and at that position particle possess horizontal component of velocity only. Given \[{{u}_{vertical}}=u\sin \theta =80\Rightarrow u=\frac{80}{\sin {{30}^{o}}}=160\,m/s\] \[\therefore \,\,\,\,{{u}_{horizontal}}=u\cos \theta =160\,\,\cos {{30}^{o}}=80\sqrt{3}\,m/s.\] Problem 9. A particle is projected from point O with velocity u in a direction making an angle \[\alpha \] with the horizontal. At any instant its position is at point P at right angles to the initial direction of projection. Its velocity at point P is 
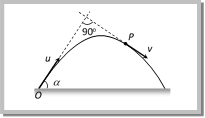(a) \[u\text{ }tan\,\alpha \] (b) \[u\text{ }cot\,\alpha \] (c) \[u\text{ }cosec\,\alpha \] (d) \[u\text{ }sec\,\alpha \] Solution: (b) Horizontal velocity at point \['O'=u\cos \alpha \] Horizontal velocity at point \['P'=v\sin \alpha \] 
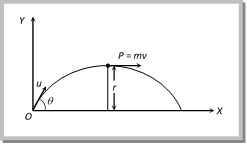\[L=mvr\] \[\left[ \text{Here }r=H=\frac{{{u}^{2}}{{\sin }^{2}}\theta }{2g} \right]\] \[\therefore \,\,\,\,\,\,\,L=m\,\,u\cos \theta \,\frac{{{u}^{2}}{{\sin }^{2}}\theta }{2g}=\frac{m\,\,{{u}^{3}}\cos \theta {{\sin }^{2}}\theta }{2g}\] Sample problems based on momentum and angular momentum Problem 14. A body of mass 0.5 kg is projected under gravity with a speed of 98 m/s at an angle of 30o with the horizontal. The change in momentum (in magnitude) of the body is [MP PET 1997] (a) 24.5 N?s (b) 49.0 N?s (c) 98.0 N?s (d) 50.0 N?s Solution: (b) Change in momentum between complete projectile motion \[= 2mu sin\,\theta \] \[=2\times 0.5\times 98\times \sin 30{}^\circ \]= 49 N?s. Problem 15. A particle of mass 100 g is fired with a velocity 20 m sec?1 making an angle of 30o with the horizontal. When it rises to the highest point of its path then the change in its momentum is (a) \[\sqrt{3}kg\,m\,{{\sec }^{-1}}\] (b) \[1/2 kg m se{{c}^{1}}\] (c) \[\sqrt{2}\,kg\,m\,{{\sec }^{-1}}\] (d) \[1\text{ }kg\text{ }m\text{ }se{{c}^{1}}\] Solution: (d) Horizontal momentum remains always constant So change in vertical momentum (D\[\vec{p}\]) = Final vertical momentum ? Initial vertical momentum \[=0-mu\sin \theta \] \[|\Delta P|\,=0.1\times 20\times \sin {{30}^{o}}\] \[=1\,kg\,m/sec\]. Problem 16. Two equal masses (m) are projected at the same angle (q) from two points separated by their range with equal velocities (v). The momentum at the point of their collision is (a) Zero (b) \[2\text{ }mv\text{ }cos\,\theta \] (c) \[\,2\text{ }mv\text{ }cos\,\theta \] (d) None of these Solution: (a) Both masses will collide at the highest point of their trajectory with equal and opposite momentum. So net momentum of the system will be zero. 
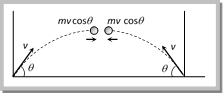Problem 17. A particle of mass m is projected with velocity v making an angle of \[{{45}^{o}}\] with the horizontal. The magnitude of the angular momentum of the particle about the point of projection when the particle is at its maximum height is (where g = acceleration due to gravity) [MP PMT 1994; UPSEAT 2000; MP PET 2001] (a) Zero (b) \[m{{v}^{3}}/(4\sqrt{2}g)\] (c) \[m{{v}^{3}}/(\sqrt{2}g)\] (d) \[m{{v}^{2}}/2g\] Solution: (b) \[L=\frac{m\,\,{{u}^{3}}\cos \theta {{\sin }^{2}}\theta }{2g}=\frac{m{{v}^{3}}}{(4\sqrt{2}\,g)}\] \[[As\,\theta = 4{{5}^{o}}]\] Problem 18. A body is projected from the ground with some angle to the horizontal. What happens to the angular momentum about the initial position in this motion [AIIMS 2000] (a) Decreases (b) Increases (c) Remains same (d) First increases and then decreases Solution: (b) Problem 19. In case of a projectile, where is the angular momentum minimum (a) At the starting point (b) At the highest point (c) On return to the ground (d) At some more... 
then \[{{t}_{1}}+{{t}_{2}}=\frac{2u\sin \theta }{g}=\] time of flight or \[u\sin \theta =\frac{g({{t}_{1}}+{{t}_{2}})}{2}\] and height of the point p is given by \[h=u\sin \theta \,{{t}_{1}}-\frac{1}{2}gt_{1}^{2}\] \[h=g\frac{({{t}_{1}}+{{t}_{2}})}{2}{{t}_{1}}-\frac{1}{2}gt_{1}^{2}\] by solving \[h=\frac{g\,{{t}_{1}}{{t}_{2}}}{2}\] (iv) If B and C are at the same level on trajectory and the time difference between these two points is \[{{t}_{1}}\], similarly A and D are also at the same level and the time difference between these two positions is \[{{t}_{2}}\] then 
\[t_{2}^{2}-t_{1}^{2}=\frac{8h}{g}\] Sample problems based on time of flight Problem 20. For a given velocity, a projectile has the same range R for two angles of projection if t1 and t2 are the times of flight in the two cases then [KCET 2003] (a) \[{{t}_{1}}{{t}_{2}}\propto \,{{R}^{2}}\] (b) \[{{t}_{1}}{{t}_{2}}\propto \,R\] (c) \[{{t}_{1}}{{t}_{2}}\propto \,\frac{1}{R}\] (d) \[{{t}_{1}}{{t}_{2}}\propto \,\frac{1}{{{R}^{2}}}\] Solution: (b) As we know for complementary angles \[{{t}_{1}}{{t}_{2}}=\frac{2R}{g}\] \ \[{{t}_{1}}{{t}_{2}}\propto R\]. Problem 21. A body is thrown with a velocity of 9.8 m/s making an angle of \[{{30}^{o}}\] with the horizontal. It will hit the ground after a time [JIPMER 2001, 2002; KCET (Engg.) 2001] (a) 1.5 s (b) 1 s (c) 3 s (d) 2 s Solution: (b) \[T=\frac{2u\sin \theta }{g}=\frac{2\times 9.8\times \sin {{30}^{o}}}{9.8}=1\,\,\sec \] Problem 22. Two particles are separated at a horizontal distance x as shown in figure. They are projected at the same time as shown in figure with different initial speed. The time after which the horizontal distance between the particles become zero is [CBSE PMT 1999]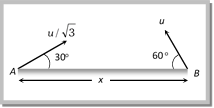 
(a) \[u/2x\] (b) \[x/u\] (c) \[2u/x\] (d) \[u/x\] Solution: (b) Let \[{{x}_{1}}\,\,and\,\,{{x}_{2}}\] are the horizontal distances travelled by particle A and B respectively in time t. \[{{x}_{1}}=\frac{u}{\sqrt{3}}.\cos 30{}^\circ \times t\] ?.. (i) and \[{{x}_{2}}=u\cos {{60}^{o}}\times t\] ?? (ii) \[{{x}_{1}}+{{x}_{2}}=\frac{u}{\sqrt{3}}.\cos {{30}^{o}}\times t+u\cos {{60}^{o}}\times t=ut\] \[\Rightarrow \,\,\,x=ut\] \[\therefore \,\,t=x/u\] Problem 23. A particle is projected from a point O with a velocity u in a direction making an angle a upward with the horizontal. After some time at point P it is moving at right angle with more... 
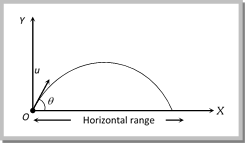\[R=u\cos \theta \times T\]\[=\,\]\[u\cos \theta \times (2u\sin \theta /g)\]\[=\frac{{{u}^{2}}\,\sin \,2\theta }{g}\] \[R=\frac{{{u}^{2}}\,\sin \,2\theta }{g}\] (i) Range of projectile can also be expressed as: \[\operatorname{R} = u cos\,\theta \,\,\times \, T =u\cos \theta \frac{2u\sin \theta }{g}=\frac{2\,u\cos \theta \,\,u\sin \theta }{g}=\frac{\text{2}{{\text{u}}_{\text{x}}}{{u}_{y}}}{\text{g}}\] \ \[R=\frac{\text{2}{{\text{u}}_{\text{x}}}{{u}_{y}}}{\text{g}}\] (where \[{{\operatorname{u}}_{x}}\,and {{u}_{y}}\] are the horizontal and vertical component of initial velocity) (ii) If angle of projection is changed from \[\theta \] to \[\theta =(90\theta )\] then range remains unchanged. 
\[R'=\frac{{{u}^{2}}\sin 2\theta \,'\,}{g}=\frac{{{u}^{2}}\sin [2({{90}^{o}}-\theta )]}{g}=\frac{{{u}^{2}}\sin 2\theta \,}{g}=R\] So a projectile has same range at angles of projection q and (90 ? q), though time of flight, maximum height and trajectories are different. These angles q and \[{{90}^{o}}\theta \] are called complementary angles of projection and for complementary angles of projection ratio of range \[\frac{{{R}_{1}}}{{{R}_{2}}}=\frac{{{u}^{2}}\sin \,2\theta /g}{{{u}^{2}}\sin \,[2\,({{90}^{o}}-\theta )]\,/g}=1\Rightarrow \frac{{{R}_{1}}}{{{R}_{2}}}=1\] (iii) For angle of projection \[{{\theta }_{1}}= (45 \alpha )\] and \[{{\theta }_{2}}=(45\text{ }+\alpha )\], range will be same and equal to \[{{\operatorname{u}}^{2}}\,cos 2a/g.\] \[{{\theta }_{1}}\,and\,{{\theta }_{2}}\] are also the complementary angles.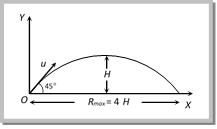 
(iv) Maximum range: For range to be maximum \[\frac{dR}{d\theta }=0\]\[\Rightarrow \] \[\frac{d}{d\theta }\left[ \frac{{{u}^{2}}\,\sin \,2\theta }{g} \right]\,=\,0\] \[\Rightarrow cos 2\,\theta = 0\] i.e. \[2\theta =\text{ }{{90}^{o}}\,\Rightarrow ~\theta =\text{ }{{45}^{o}}~and~~{{R}_{max}}=\text{ }\left( {{u}^{2}}/g \right)\] i.e., a projectile will have maximum range when it is projected at an angle of 45o to the horizontal and the maximum range will be \[\left( {{u}^{2}}/g \right)\]. When the range is maximum, the height H reached by the projectile \[H=\frac{{{u}^{2}}{{\sin }^{2}}\theta }{2g}=\frac{{{u}^{2}}{{\sin }^{2}}45}{2g}=\frac{{{u}^{2}}}{4g}=\frac{{{R}_{\max }}}{4}\] i.e., if a person can throw a projectile to a maximum distance \[{{R}_{max}},\] The maximum height to which it will rise is \[\left( \frac{{{R}_{\max }}}{4} \right)\]. (v) Relation between horizontal range and maximum height: \[R=\frac{{{u}^{2}}\sin 2\theta }{g}\] and \[H=\,\frac{{{u}^{2}}{{\sin }^{2}}\theta }{2g}\] \[\therefore \,\,\,\,\frac{R}{H}=\frac{{{u}^{2}}\sin 2\theta /g}{{{u}^{2}}{{\sin }^{2}}\theta /2g}=4\cot \theta \] \[\Rightarrow \,\,R=4H\cot \theta \] (vi) If in case of projectile motion range R is n times the maximum height H i.e. R = nH Þ \[\frac{{{u}^{2}}\sin 2\theta }{g}=n\,\frac{{{u}^{2}}{{\sin }^{2}}\theta }{2g}\] Þ \[\tan \,\theta \,=[4/n]\] or \[\theta ={{\tan }^{-1}}[4/n]\] The angle of projection is given by \[\theta ={{\tan }^{-1}}[4/n]\] Note: q If R = H then \[\theta ={{\tan }^{-1}}(4)\] or \[\theta ={{76}^{o}}\]. If R = 4H then \[\theta ={{\tan }^{-1}}(1)\] or \[\theta ={{45}^{o}}\]. Sample problem based on horizontal range Problem 28. A boy playing on the roof of a 10m high building throws a ball with a speed of 10 m/s at an angle of \[{{30}^{o}}\] with the horizontal. How far from the throwing point will the ball be at the height of 10 m from the ground (g = \[10\text{ }m/{{s}^{2}},\text{ }sin\text{ }{{30}^{o}}=\frac{1}{2}\], \[\cos \,{{30}^{o}}\,=\,\frac{\sqrt{3}}{2}\]) [AIEEE 2003] (a) 8.66 m (b) 5.20 m (c) 4.33 m (d) 2.60 m 
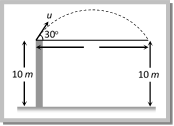Solution: (a) Simply we have more... 
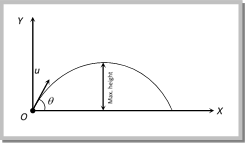So, by using \[{{v}^{2}}={{u}^{2}}+2as\] \[0={{(u\sin \theta )}^{2}}-2gH\] \[H=\frac{{{u}^{2}}{{\sin }^{2}}\theta }{2g}\] (i) Maximum height can also be expressed as \[H=\frac{u_{y}^{2}}{2g}\] (where \[{{u}_{y}}\] is the vertical component of initial velocity). (ii) \[{{H}_{\max }}=\frac{{{u}^{2}}}{2g}\] (when \[{{\sin }^{2}}\,\theta = max = 1\] i.e., \[\theta = 9{{0}^{o}}\]) i.e., for maximum height body should be projected vertically upward. So it falls back to the point of projection after reaching the maximum height. (iii) For complementary angles of projection \[\theta \,\,and\, 9{{0}^{o}}\theta \] Ratio of maximum height = \[\frac{{{H}_{1}}}{{{H}_{2}}}=\frac{{{u}^{2}}{{\sin }^{2}}\theta /2g}{{{u}^{2}}{{\sin }^{2}}({{90}^{o}}-\theta )2g}\] \[=\frac{{{\sin }^{2}}\theta }{{{\cos }^{2}}\theta }\] \[={{\tan }^{2}}\theta \] \[\therefore \,\,\,\,\,\frac{{{H}_{1}}}{{{H}_{2}}}={{\tan }^{2}}\theta \] Sample problem based on maximum height Problem 49. A cricketer can throw a ball to a maximum horizontal distance of 100 m. With the same effort, he throws the ball vertically upwards. The maximum height attained by the ball is [UPSEAT 2002] (a) 100 m (b) 80 m (c) 60 m (d) 50 m Solution: (d) \[{{R}_{\max }}=\frac{{{u}^{2}}}{g}=100\,m\] (when \[\theta =45{}^\circ \]) \[\therefore \,\,\,\,\,{{u}^{2}}=100\times 10=1000\] \[{{H}_{\max }}=\frac{{{u}^{2}}}{2g}=\frac{1000}{2\times 10}=50\,\,metre.\] (when \[\theta =90{}^\circ \]) Problem 50. A ball thrown by one player reaches the other in 2 sec. the maximum height attained by the ball above the point of projection will be about [Pb. PMT 2002] (a) 10 m (b) 7.5 m (c) 5 m (d) 2.5 m Solution: (c) \[T=\frac{2u\sin \theta }{g}=2\,sec\] (given) \[\therefore \,\,\,\,\,u\sin \theta =10\] Now \[H=\frac{{{u}^{2}}{{\sin }^{2}}\theta }{2g}=\frac{{{(10)}^{2}}}{2\times 10}=5\,m.\] Problem 51. Two stones are projected with the same magnitude of velocity, but making different angles with horizontal. The angle of projection of one is p/3 and its maximum height is Y, the maximum height attained by the other stone with as p/6 angle of projection is [J & K CET 2000] (a) Y (b) 2 Y (c) 3 Y (d) \[\frac{Y}{3}\] Solution: (d) When two stones are projected with same velocity then for complementary angles \[\theta \] and \[(9{{0}^{o}}\theta )\] Ratio of maximum heights: \[\frac{{{H}_{1}}}{{{H}_{2}}}={{\tan }^{2}}\theta ={{\tan }^{2}}\frac{\pi }{3}=3\Rightarrow {{H}_{2}}=\frac{{{H}_{1}}}{3}=\frac{Y}{3}\] Problem 52. If the initial velocity of a projectile be doubled. Keeping the angle of projection same, the maximum height reached by it will (a) Remain the same (b) Be doubled (c) Be quadrupled (d) Be halved Solution: (c) \[H=\frac{{{u}^{2}}\sin 2\theta }{2g}\] \[\therefore \,\,\,\,H\propto {{u}^{2}}\] [As \[\theta =cons\tan t\]] If initial velocity of a projectile be doubled then H will becomes 4 times. Problem 53. Pankaj and Sudhir are playing with two different balls of masses m and 2m respectively. If Pankaj throws his ball vertically up and Sudhir at an angle \[\theta \], both of them stay in our view for the same period. The height attained by the two balls are in the ratio (a) 2 : 1 (b) 1 : 1 (c) \[1:cos\,\theta \] (d) \[1:sec\,\theta \] 
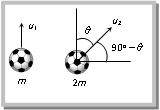Solution: (b) Time of flight for more... 
The component of g along the plane is \[g\sin \alpha \] and perpendicular to the plane is \[g\cos \alpha \] as shown in the figure i.e. \[{{a}_{||}}=-g\sin \alpha \] and \[{{a}_{\bot }}=g\cos \alpha \]. Therefore the particle decelerates at a rate of \[g\sin \alpha \] as it moves from O to P. (1) Time of flight: We know for oblique projectile motion \[T=\frac{2u\sin \theta }{g}\] or we can say \[T=\frac{2{{u}_{\bot }}}{{{a}_{\bot }}}\] \[\therefore \,\,\,\,Time\text{ }of\text{ }flight\text{ }on\text{ }an\text{ }inclined\text{ }plane\,\,T=\frac{2u\sin \theta }{g\cos \alpha }\] (2) Maximum height: We know for oblique projectile motion \[H=\frac{{{u}^{2}}{{\sin }^{2}}\theta }{2g}\] or we can say \[H=\frac{u_{\bot }^{2}}{2{{a}_{\bot }}}\] \[\therefore \] Maximum height on an inclined plane \[H=\frac{{{u}^{2}}{{\sin }^{2}}\theta }{2g\cos \alpha }\] (3) Horizontal range: For one dimensional motion \[s=ut+\frac{1}{2}a{{t}^{2}}\] Horizontal range on an inclined plane \[R={{u}_{||}}T+\frac{1}{2}{{a}_{||}}{{T}^{2}}\] \[R=u\cos \theta \,T-\frac{1}{2}g\sin \alpha \,\,{{T}^{2}}\] \[R=u\cos \theta \,\left( \frac{2u\sin \theta }{g\cos \alpha } \right)-\frac{1}{2}g\sin \alpha \,{{\left( \frac{2u\sin \theta }{g\cos \alpha } \right)}^{2}}\] By solving \[R=\frac{2{{u}^{2}}}{g}\,\frac{\sin \theta \,\cos (\theta +\alpha )}{{{\cos }^{2}}\alpha }\] (i) Maximum range occurs when \[\theta =\frac{\pi }{4}-\frac{\alpha }{2}\] (ii) The maximum range along the inclined plane when the projectile is thrown upwards is given by \[{{R}_{\max }}=\frac{{{u}^{2}}}{g\,(1+\sin \alpha )}\] (iii) The maximum range along the inclined plane when the projectile is thrown downwards is given by \[{{R}_{\max }}=\frac{{{u}^{2}}}{g\,(1-\sin \alpha )}\] Sample problem based on inclined projectile Problem 77. For a given velocity of projection from a point on the inclined plane, the maximum range down the plane is three times the maximum range up the incline. Then, the angle of inclination of the inclined plane is (a) \[{{30}^{o}}\] (b) \[{{45}^{o}}\] (c) \[{{60}^{o}}\] (d) \[{{90}^{o}}\] Solution: (a) Maximum range up the inclined plane \[{{({{R}_{\max }})}_{up}}=\frac{{{u}^{2}}}{g(1+\sin \alpha )}\] Maximum range down the inclined plane \[{{({{R}_{\max }})}_{down}}=\frac{{{u}^{2}}}{g(1-\sin \alpha )}\] and according to problem: \[\frac{{{u}^{2}}}{g(1-\sin \alpha )}=3\times \frac{{{u}^{2}}}{g(1+\sin \alpha )}\] By solving \[\alpha =\text{ }{{30}^{o}}\] Problem 78. A shell is fired from a gun from the bottom of a hill along its slope. The slope of the hill is \[\alpha =\text{ }{{30}^{o}}\], and the angle of the barrel to the horizontal \[\beta = 6{{0}^{o}}\]. The initial velocity v of the shell is 21 m/sec. Then distance of point from the gun at which shell will fall (a) 10 m (b) 20 m (c) 30 m (d) 40 m Solution: (c) Here u = 21 m/sec, \[\alpha = 3{{0}^{o}},\,\,q=\beta \,\alpha = 6{{0}^{o}} 3{{0}^{o}}= 3{{0}^{o}}\] Maximum range \[R=\frac{2{{u}^{2}}}{g}\,\frac{\sin \theta \,\cos (\theta +\alpha )}{{{\cos }^{2}}\alpha }=\frac{2\,\times {{(21)}^{2}}\times \sin {{30}^{o}}\cos {{60}^{o}}}{9.8\times {{\cos }^{2}}{{30}^{o}}}=30\,\,m\] more... 
Variables of Circular Motion. (1) Displacement and Distance: When particle moves in a circular path describing an angle q during time t (as shown in the figure) from the position A to the position B, we see that the magnitude of the position vector \[\vec{r}\] (that is equal to the radius of the circle) remains constant. i.e., \[\left| {{{\vec{r}}}_{1}} \right|\,=\,\left| {{{\vec{r}}}_{2}} \right|=r\] and the direction of the position vector changes from time to time. (i) Displacement: The change of position vector or the displacement \[\Delta \vec{r}\] of the particle from position A to the position B is given by referring the figure. \[\Delta \,\vec{r}={{\vec{r}}_{2}}-{{\vec{r}}_{1}}\] \[\Rightarrow \,\,\Delta r=\,\left| \Delta \vec{r} \right|\,=\,\left| {{{\vec{r}}}_{2}}-{{{\bar{r}}}_{1}} \right|\,\,\,\,\,\Delta r=\,\sqrt{r_{1}^{2}+r_{2}^{2}-2{{r}_{1}}{{r}_{2}}\,\cos \theta }\]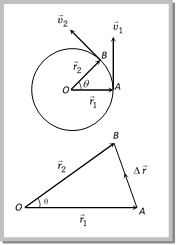 
Putting \[{{r}_{1}}={{r}_{2}}=r\] we obtain \[\Delta r=\sqrt{{{r}^{2}}+{{r}^{2}}-2r.r\,\cos \theta }\] \[\Rightarrow \Delta r=\sqrt{2{{r}^{2}}\left( 1-\cos \theta \right)}\,=\,\sqrt{2{{r}^{2}}\left( 2{{\sin }^{2}}\frac{\theta }{2} \right)}\] \[\Delta \,r=2r\,\sin \frac{\theta }{2}\] (ii) Distance: The distanced covered by the particle during the time t is given as \[\operatorname{d} = length of the arc AB = r\,\theta \] (iii) Ratio of distance and displacement: \[\frac{d}{\Delta r}=\frac{r\theta }{2r\,\sin \theta /2}=\frac{\theta }{2}\text{cosec}\,(\theta /2)\] Sample problems based on distance and displacement Problem 80. A particle is rotating in a circle of radius r. The distance traversed by it in completing half circle would be (a) r (b) \[\pi r\] (c) \[2\pi r\] (d) Zero Solution: (b) Distance travelled by particle = Semi-circumference \[=\pi r\]. Problem 81. An athlete completes one round of a circular track of radius 10 m in 40 sec. The distance covered by him in 2 min 20 sec is [Kerala PMT 2002] (a) 70 m (b) 140 m (c) 110 m (d) 220 m Solution: (d) \[\text{No}\text{. of revolution}\,\text{(}n\text{)}=\frac{\text{Total time of mo}\text{tion}}{\text{Time}\,\text{period}}=\frac{140\,\sec }{40\,\sec }=3.5\,\] Distance covered by an athlete in revolution \[=\,\,\,n\,(2\pi \,r)=3.5\,(2\pi \,r)=3.5\times 2\times \frac{22}{7}\times 10=220\,m.\] Problem 82. A wheel covers a distance of 9.5 km in 2000 revolutions. The diameter of the wheel is [RPMT 1999; BHU 2000] (a) 15 (b) 7.5 m (c) 1.5 m (d) 7.5 m Solution: (c) Distance \[=n\,(2\pi \,r)\Rightarrow 9.5\times {{10}^{3}}=2000\times (\pi D)\Rightarrow D=\frac{9.5\times {{10}^{3}}}{2000\times \pi }=1.5\,m.\] (2) Angular displacement (q): The angle turned by a body moving on a circle from some more... 
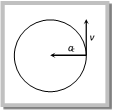(4) Direction of centripetal acceleration: It is always the same as that of \[\Delta \overrightarrow{\upsilon }\]. When Dt decreases, Dq also decreases. Due to which \[\Delta \vec{\upsilon }\] becomes more and more perpendicular to \[\overrightarrow{\upsilon }\]. When \[\Delta t\to 0\], \[\Delta \overrightarrow{\upsilon }\] becomes perpendicular to the velocity vector. As the velocity vector of the particle at an instant acts along the tangent to the circular path, therefore \[\Delta \overrightarrow{\upsilon }\] and hence the centripetal acceleration vector acts along the radius of the circular path at that point and is directed towards the centre of the circular path. Sample problems based on centripetal acceleration Problem 100. If a cycle wheel of radius 4 m completes one revolution in two seconds. Then acceleration of the cycle will be [Pb. PMT 2001] (a) \[{{\pi }^{2}}m/{{s}^{2}}\] (b) \[2{{\pi }^{2}}m/{{s}^{2}}\] (c) \[4{{\pi }^{2}}m/{{s}^{2}}\] (d) \[8\pi \,m/{{s}^{2}}\] Solution: (c) Given \[r=4\,m\] and \[T=2\,\,\sec onds.\] \[\therefore \,\,\,\,{{a}_{c}}=\frac{4{{\pi }^{2}}}{{{T}^{2}}}r=\frac{4{{\pi }^{2}}}{{{(2)}^{2}}}4=4{{\pi }^{2}}\,m/{{s}^{2}}\] Problem 101. A stone is tied to one end of a spring 50 cm long is whirled in a horizontal circle with a constant speed. If the stone makes 10 revolutions in 20 s, what is the magnitude of acceleration of the stone [Pb. PMT 2000] (a) \[493 cm/se{{c}^{2}}\] (b) \[720\text{ }cm/se{{c}^{2}}\] (c) \[860 cm/se{{c}^{2}}\] (d) \[990 cm/se{{c}^{2}}\] Solution: (a) \[=\frac{\text{Total time}}{\text{No}\text{. of revolution}}=\frac{20}{10}=2\,sec\] \[\therefore \,\,\,\,\,{{a}_{c}}=\frac{4{{\pi }^{2}}}{{{T}^{2}}}.r=\frac{4{{\pi }^{2}}}{{{(2)}^{2}}}\times (1/2)\,m/{{s}^{2}}=4.93\,m/{{s}^{2}}=493\,cm/{{s}^{2}}\] Problem 102. A particle moves with a constant speed v along a circular path of radius r and completes the circle in time T. What is the acceleration of the particle [Orissa JEE 2002] (a) \[mg\] (b) \[\frac{2\pi v}{T}\] (c) \[\frac{\pi {{r}^{2}}}{T}\] (d) \[\frac{\pi {{v}^{2}}}{T}\] Solution: (b) \[{{a}_{c}}=\frac{{{v}^{2}}}{r}={{\omega }^{2}}r=v\omega =v\,\left( \frac{2\pi }{T} \right)=\frac{2\pi \,v}{T}\] Problem 103. If the speed of revolution of a particle on the circumference of a circle and the speed gained in falling through a distance equal to half the radius are equal, then the centripetal acceleration will be (a) \[\frac{g}{2}\] (b) \[\frac{g}{4}\] (c) \[\frac{g}{3}\] (d) g Solution: (d) Speed gain by body falling through a distance h is equal to \[v=\sqrt{2gh}=\sqrt{2g\frac{r}{2}}\] [As \[h=\frac{r}{2}\] given] \[\Rightarrow v=\sqrt{gr}\Rightarrow \,\,\frac{{{v}^{2}}}{r}=g\] Problem 104. Two cars going round curve with speeds one at 90 km/h and other at 15 km/h. Each car experiences same acceleration. The radii of curves are in the ratio of [EAMCET (Med.) 1998] (a) 4 : 1 (b) 2 : 1 (c) 16 : 1 (d) 36 : 1 Solution: (d) Centripetal acceleration \[=\frac{v_{1}^{2}}{{{r}_{1}}}=\frac{v_{2}^{2}}{{{r}_{2}}}\] (given) \[\therefore \,\,\,\,\frac{{{r}_{1}}}{{{r}_{2}}}={{\left( \frac{{{v}_{1}}}{{{v}_{2}}} \right)}^{2}}={{\left( \frac{90}{15} \right)}^{2}}=\frac{36}{1}\] Problem 105. A wheel of radius \[0.20\,\,m\] is accelerated from rest with an angular acceleration of \[1\ rad/{{s}^{2}}\]. After a rotation of \[{{90}^{o}}\] the radial acceleration of a particle more... 
Example: (i) When an electron revolve around the nucleus in hydrogen atom in a particular orbit, it neither absorb nor emit any energy means its energy remains constant. (ii) When a satellite established once in a orbit around the earth and it starts revolving with particular speed, then no fuel is required for its circular motion. Sample problem based on work done Problem 121. A particle does uniform circular motion in a horizontal plane. The radius of the circle is 20 cm. The centripetal force acting on the particle is 10 N. It?s kinetic energy is (a) 0.1 Joule (b) 0.2 Joule (c) 2.0 Joule (d) 1.0 Joule Solution: (d) \[\frac{m\,{{v}^{2}}}{r}=10\,N\] (given) Þ \[m\,{{v}^{2}}=10\times r\] \[=10\times 0.2=2\] Kinetic energy \[\frac{1}{2}m\,{{v}^{2}}=\frac{1}{2}(2)=1\,Joule.\] Problem 122. A body of mass 100 g is rotating in a circular path of radius r with constant velocity. The work done in one complete revolution is [AFMC 1998] (a) 100 r Joule (b) (r/100) Joule (c) (100/r) Joule (d) Zero Solution: (d) Because in uniform circular motion work done by the centripetal force is always zero. Problem 123. A particle of mass m is describing a circular path of radius r with uniform speed. If L is the angular momentum of the particle about the axis of the circle, the kinetic energy of the particle is given by [CPMT 1995] (a) \[{{L}^{2}}/m{{r}^{2}}\] (b) \[{{L}^{2}}/2m{{r}^{2}}\] (c) \[2{{L}^{2}}/m{{r}^{2}}\] (d) \[m{{r}^{2}}L\] Solution: (b) Rotational kinetic energy \[E=\frac{{{L}^{2}}}{2I}\]\[=\frac{{{L}^{2}}}{2m\,{{r}^{2}}}\] (As for a particle \[I=m\,{{r}^{2}}\]) Skidding of Vehicle on a Level Road. When a vehicle turns on a circular path it requires centripetal force. If friction provides this centripetal force then vehicle can move in circular path safely if \[\operatorname{Friction} force\ge Required centripetal force\] \[\mu \,mg\ge \frac{m{{v}^{2}}}{r}\] \[\therefore \,\,\,\,\,\,\,\,\,{{v}_{safe}}\le \sqrt{\mu rg}\]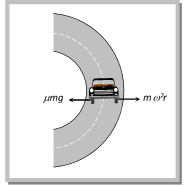 
This is the maximum speed by which vehicle can turn in a circular path of radius r, where coefficient of friction between the road and tyre is m. Sample problem based on skidding of vehicle on a level road Problem 124. Find the maximum velocity for overturn for a car moved on a circular track of radius \[100m\]. The coefficient of friction between the road and tyre is \[0.2\] [CPMT 1996] (a) \[0.14\ m/s\] (b) \[140\ m/s\] (c) \[1.4\ km/s\] (d) \[14\ m/s\] Solution: (d) \[{{v}_{\max }}=\sqrt{\mu \,r\,g}\]\[=\sqrt{0.2\times 100\times 10}\]\[=10\sqrt{2}\]\[=14\,m/s\] Problem 125. When the road is dry and the coefficient of friction is \[\mu \], the maximum speed of a car in a circular path is \[10\ m/s\]. If the road becomes wet and \[{\mu }'=\frac{\mu }{2}\], what is the maximum speed permitted (a) \[5\ m/s\] (b) \[10\ m/s\] (c) \[10\sqrt{2}\ m/s\] (d) \[5\sqrt{2}\ m/s\] Solution : (d) \[v\propto \sqrt{\mu }\Rightarrow \frac{{{v}_{2}}}{{{v}_{1}}}=\sqrt{\frac{{{\mu more... 
You need to login to perform this action.
You will be redirected in
3 sec
