Current Affairs JEE Main & Advanced

Category : JEE Main & Advanced

(1) Circumcircle of a triangle and its radius

(i) Circumcircle : The circle which passes through the angular points of a triangle is called its circumcircle. The centre of this circle is the point of intersection of perpendicular bisectors of the sides and is called the circumcentre. Its radius is always denoted by R. The circumcentre may lie within, outside or upon one of the sides of the triangle.

(ii) Circum-radius : The circum-radius of a \[\Delta ABC\]is given by   

(a)  \[\frac{a}{2\sin A}=\frac{b}{2\sin B}=\frac{c}{2\sin C}=R\] 

(b)  \[R=\frac{abc}{4\Delta }\]  \[[\Delta =\]area of \[\Delta ABC\]]

(2)  Inscribed circle or in-circle of a triangle and its radius

(i)  In-circle or inscribed circle : The circle which can be inscribed within a triangle so as to touch each of its sides is called its inscribed circle or in circle. The centre of this circle is the point of intersection of the bisectors of the angles of the triangle. The radius of this circle is always denoted by \[r\] and is equal to the length of the perpendicular from its centre to any one of the sides of triangle.

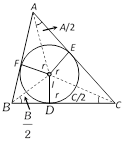
(ii) In-radius : The radius r of the inscribed circle of a triangle ABC is given by

(a) \[r=\frac{\Delta }{s}\]    

(b)  \[r=4R\sin \frac{A}{2}\sin \frac{B}{2}\sin \frac{C}{2}\]

(c) \[r=(s-a)\tan \frac{A}{2},\,\,r=(s-b)\tan \frac{B}{2},\,\,r=(s-c)\tan \frac{C}{2}\]

(d)  \[r=\frac{a\sin \frac{B}{2}\sin \frac{C}{2}}{\cos \frac{A}{2}},r=\frac{b\sin \frac{A}{2}\sin \frac{C}{2}}{\cos \frac{B}{2}},r=\frac{c\sin \frac{B}{2}\sin \frac{A}{2}}{\cos \frac{C}{2}}\]               

(e)  \[\cos A+\cos B+\cos C=1+\frac{r}{R}\]  

(3) Escribed circles of a triangle and their radii

(i) Escribed circle : The circle which touches the side BC and two sides AB and AC produced of a triangle ABC is called the escribed circle opposite to the angle A. Its radius is denoted by \[{{r}_{1}}\]. Similarly, \[{{r}_{2}}\] and \[{{r}_{3}}\] denote the radii of the escribed circles opposite to the angles B and C respectively.

The centres of the escribed circles are called the ex-centres. The centre of the escribed circle opposite to the angle A is the point of intersection of the external bisectors of angles B and C. The internal bisectors of angle A also passes through the same point. The centre is generally denoted by I₁.

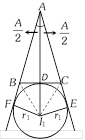
(ii) Radii of ex-circles

In any \[\Delta ABC\], we have

(a) \[{{r}_{1}}=\frac{\Delta }{s-a},{{r}_{2}}=\frac{\Delta }{s-b},{{r}_{3}}=\frac{\Delta }{s-c}\]

(b) \[{{r}_{1}}=s\tan \frac{A}{2},\,\,\,{{r}_{2}}=s\tan \frac{B}{2},\,\,{{r}_{3}}=s\tan \frac{C}{2}\]

(c) \[{{r}_{1}}=\frac{a\cos \frac{B}{2}\cos \frac{C}{2}}{\cos \frac{A}{2}},\,{{r}_{2}}=\frac{b\cos \frac{C}{2}\cos \frac{A}{2}}{\cos \frac{B}{2}},{{r}_{3}}=\frac{c\cos \frac{A}{2}\cos \frac{B}{2}}{\cos \frac{C}{2}}\]

(d) \[{{r}_{1}}+{{r}_{2}}+{{r}_{3}}-r=4R\]

(e) \[\frac{1}{{{r}_{1}}}+\frac{1}{{{r}_{2}}}+\frac{1}{{{r}_{3}}}=\frac{1}{r}\]

(f) \[\frac{1}{{{r}^{2}}}+\frac{1}{r_{1}^{2}}+\frac{1}{r_{2}^{2}}+\frac{1}{r_{3}^{2}}=\frac{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}{{{\Delta }^{2}}}\]

(g) \[\frac{1}{bc}+\frac{1}{ca}+\frac{1}{ab}=\frac{1}{2Rr}\]           

(h) \[{{r}_{1}}{{r}_{2}}+{{r}_{2}}{{r}_{3}}+{{r}_{3}}{{r}_{1}}={{s}^{2}}\]

(i) \[\Delta =2{{R}^{2}}\sin A.\sin B.\sin C=4Rr\cos \frac{A}{2}.\cos \frac{B}{2}.\cos \frac{C}{2}\]

(j) \[{{r}_{1}}=4R\sin \frac{A}{2}\cos \frac{B}{2}\cos \frac{C}{2};{{r}_{2}}=4R\cos \frac{A}{2}.\sin \frac{B}{2}.\cos \frac{C}{2}\]

(4) Centroid (G) : Common point of intersection of medians of a triangle. Divides every median in the ratio 2:1. Always lies inside the triangle.

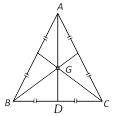
(5) Orthocentre of a triangle : The point of intersection of perpendicular drawn from the vertices on the opposite sides of a triangle is called its orthocentre.