Current Affairs 12th Class

Category : 12th Class

 

                                                                                      Relations and Functions

 

• To understand relations and functions let's consider two sets A = {1, 2, 3, 4} and B ={2,3}

Now, \[~A\times B=\{1,\,2,\,3,\,4,\}\times \{2,3\}=\{(1,\,2),\,(2,\,2),\,(3,\,2),\,(4,\,2),\,(1,\,3),\,(2,\,3),\,(3,\,3),\,(4,\,3)\}\]

Let we choose an arbitrary set:

R = [(1, 2), (2, 2), (1, 3), (4, 3)]

Then R is said to be the relation between a set A to B.

 

• Definition: Relation R is the subset of the Cartesian product\[A\times B\]. It is represented as

\[R=\{(x,\,y):x\in A\,\,\,and\,\,\,y\in B\}\]

Note: the 2nd element in the ordered pair (x, y) is the image of 1st element Sometime, it is said that a relation on the set A means the all members / elements of the relation R be the elements / members of\[A\times A\].

Solved Example

1. Let \[A=\{1,\,2,\,3\}\] and a relation R is defined as \[R=\{(x,\,y):x<y\,\,where\,\,x,\,\,y\in A\}\]

Sol. \[\because A=\{1,\,2,\,3\}\]

\[A\times A=\{(1,\,1),\,(2,\,2),\,(3,\,3),\,(2,\,1),\,(3,\,1),\,(1,\,2)\,(3,\,2),\,(1,\,3),\,(2,\,3)\}\]

\[\because \,\,\,\,\,\,\,x<y\]

\[\therefore \,\,\,\,\,\,\,R=\{(x,\,y):x<y,\,\,and\,\,x,\,y\in A\}=\{(1,\,2),\,(2,\,3),\,(1,\,3)\}.\]

Note: Let a set A has m elements and set B has n elements. Then \[n(A\times B)\] be \[m\times n\] elements so, total no. of relation from A to B or between A and B be\[{{2}^{m\,\,\times \,\,n}}\].

 

• A relation can be represented algebraically either by Roster method or set builder method.

 

• Types of relations

(i)  Void Relation: A relation R on a set be said to be void or empty relation, if no element of A is related to any elements A.

e.g A relation on set A = {1, 2, 3, 4} defined as

\[R=\{(x,y):x+y=8\}.\]

It is void relation on A because, sum of any two element of \[A\times A\] can not be 8.

(ii) Universal relation: A relation on a set A is said to be universal relation. If each element of A is related to or associated with every element of A.

(iii) Identity Relation:- A relation \[{{l}_{x}}\{(x,\,x):x\in A\}\] an a set A is said to be identity relation on A.

(iv) Reflexive relation: A relation R on the set A is said to be the reflexive relation. If each and every element of set A is associated to itself. Hence, R is reflexive iff

\[(a,\,a)\in R\,\,\forall \,\,a\in A.\]

i.e. \[aRa\,\,\,\forall \,\,a\in A\]

(v) Symmetric relation: A relation R on a set A is said to be symmetric relation iff

\[(x,\,\,y)\in R\Rightarrow (y,\,x)\in R\,\,\forall \,\,x,\,\,y\in A.\]

i.e.\[x\,R\,y\Rightarrow y\,R\,x\,\,\forall \,\,x,\,\,y\in R\]

\[\because \,\,xRy\] is read as \[x\] is R-related to \[y\].

(vi) Antisymmetric relation: A relation which is not symmetric is said to be antisymmetric relation.

(vii) Transitive relation: Let A be any non-empty set. A relation R on set A is said to be transitive

relation R iff \[(x,\,y)\in R\] and \[(y,\,z)\in R\]

then \[(x,\,z)\in R\,\,\forall \,\,x,y,z\in R.\]

i.e. \[xRy\] and \[yRz\Rightarrow xRz\,\,\forall \,\,x,y,z\in R.\]

(viii) Equivalence Relation: A relation R on a set A is said to be an equivalence relation on A iff

(i) It is reflexive i.e. \[(x,y)\in R\,\,\forall \,\,x\in R\]

(ii) It is symmetric i.e. \[(x,y)\in R\,\,\Rightarrow (x,\,y)\,\,\in \,\,\,R\,\,\forall \,\,x,\,y\in R.\]

(iii) It is transitive i.e., \[(x,y)\in R\]and\[(y,\,z)\in R\], then \[(x,\,z)\in R\]\[\forall \,x,\,\,y,\text{ }z\text{ }\in \text{ }R\]

 

Solved Example

1. Let A = {1, 2, 3, 4}

\[A\times A=\{(1,1),(2,1),(3,1),(4,1),(1,2),(2,2),(3,2),(4,2),(1,3),(2,3),(3,3),(4,3),(1,4),(2,4),(3,4),(4,4)\}\]

            \[{{R}_{1}}=\{(1,1),(2,2),(3,2),(2,3),(3,3)(4,4)\}\]

\[{{R}_{2}}=\{(2,2),(1,3),(3,3),(3,1)(1,1)\}\]

\[{{R}_{3}}=\{(1,1),(2,2),(3,4),(3,3),(4,4)\}\]

State about \[{{R}_{1}},\,\,{{R}_{2}}\]and \[{{R}_{3}}\] Are they reflexive, symmetric, antisymmetric or transitive relations?

Sol. \[{{R}_{1}}\] is symmetric as well as transitive relation for \[{{R}_{2}}.\,\,{{R}_{2}}\]is not reflexive because \[(4,4)\notin {{R}_{2}}.\] But \[{{R}_{2}}\] is symmetric as well as transitive.

Now, \[{{R}_{3}}\]is reflexive as well as antisymmetric because \[(3,4)\notin {{R}_{3}}\] but \[(4,3)\notin {{R}_{3}}.\]

 

• Function

Concept of function play a very vital role in mathematics (either pure mathematics or applied mathematics). In the secondary school classes, we will learn about real value function only.

 

• Function is defined in the following ways:

(a) Function as an operator.

(b) Function as a relation.

(c) Function as a mapping.

 

• Function as an operator

Function is an operator in which we study the relation between independent and dependent real variable/input or output variable.

 

Input

f

Output

e.g.   y=f(x)

 

 

 

• Function as a mapping

Let A and B be two non-empty sets. Each element in the set A associated with unique element in set B is said to be function or mapping from A to B.

i.e. f : A \[\to \] B. e. g. y = f(x)

x is said to be independent variable and y is said to be dependent variable.

All elements of set A is said to be domain of f and all elements of set B is said to be co-domain of f as well as all images of each element of set A in B said to be the range of the function f.

\[y=f(x)\Rightarrow f(A)\subseteq B.\]e.g.\[y=f(A)\le B.\]

 

• Function as a relation

Relation: Relation on a set is the Cartesian product of two non-empty sets.

Function is a relation but relation may be or may not be function because function has some silent features. Some silent features of a function f.

e.g. f : A\[\to \]B

(i) For every \[x\in A\], \[y\in B\] s. t \[y=f(x).\] i.e. each element of set A has image in B. But there may be an element in B which is not the image of element of A.

(ii) Same element of A can not be associated to distinct element of B. i.e. the image of each element of set A has unique. But the distinct element of A may be associated to same element of B.

 

• Types of functions

Functions are of two types: Into function and onto function (surjective function)

(i)  Into function are of two types:

(a) One-one into function (Injective function)

(b) Many-one into function

(ii) Onto function are of two types:

(a) One-one onto function (bijective function)

(b) Many-one onto function

 

• One-one function (Injective function): A function f : A\[\to \]B is said to one-one function if the images of distinct elements of X under f are distinct, i.e., for every \[{{x}_{1}},{{x}_{2}}\in A,f({{x}_{1}})=f({{x}_{2}})\] implies \[{{x}_{1}}={{x}_{2}}\]

 

• Many One function: A function f: A\[\to \]B is said to be many one iff it is not one-one. e.g. f : A\[\to \]B is defined as \[y=f(x)={{x}^{2}}\]is a many one function.

 

• Onto function or subjective function: A function f: A

                                                                        

• B is said to be onto function (surjective function) iff each element of B is the image of some element of A under f, i.e. for every
• , there exists an element x in A such that f(x) = y i.e range of f = co-domain off.

 

 

 

• One-one onto function (or bijective function): A function f: A\[\to \]B is said to be one-one onto or bijective function iff distinct element of A has distinct images in B as well as range of f is equal to the domain of fe. f (A) = B. e.g. A function f : A\[\to \]B is defined as y = f (x) = x is one-one onto function.

 

• Some important functions :

1. Even function: A function\[y=f(x)\] is said to be even if\[f(-x)=f(x)\,\,\forall \,\,x\] in the domain of f. e.g \[y=f(x)={{x}^{2}}\] is an even function.
2. Odd function: A function\[y=f(x)\] is said to be odd function of if\[f(-x)=-f(x),\forall \,\,x\]in the domain of f. e.g.

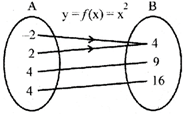
 \[y=f(x)={{x}^{3}}\] is an odd function.

 

• Some important results about even & odd functions

(i) A given function can be expressed as the sum of an even and odd function. It can be written as

\[f(x)=\left\{ \frac{1}{2}[f(x)+f(-x)]+\frac{1}{2}[f(x)-f(-x)] \right\}\]

where\[f(x)+f(-x)\] is said to be even function and\[f(x)-f(-x)\] is the odd function.

(ii) \[f(x)=0\]is the only function which is both even and odd function.

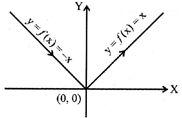
(iii) Graph of the even function is symmetric about they-axis.

(iv) Graph of the odd function is symmetric about the origin i.e

(a) lf\[f(x)\] is an even function then\[f'(x)\] is an odd function provided\[f(x)\] is differentiable on R.

(b) lf\[f(x)\] is an odd function then\[f'(x)\] is an even function provided\[f(x)\] is differentiable on R.

 

• List of some standard functions:

1. Constant function
2. Square function
3. Identity function
4. Linear function
5. Cube function
6. Reciprocal function
7. Step function
8. Modulus function
9. Logarithmic function
10. Exponential function
11. Greatest integer function
12. Polynomial function
13. Polynomial ratio function
14. Trigonometric function
15. Inverse function.

 

• Explicit function: A function \[y=f(x)\] is said to be explicit function if the dependent variable y can be expressed perfectly in the term of independent variable x only. e.g

(i) \[y=f(x)={{x}^{2}}+\log x\]

(ii) \[y=f(x)={{x}^{3}}+{{\sin }^{2}}x\]

 

• Implicit function : A function \[y=f(x)\] is said to be implicit function if the dependent variable y cannot be expressed in the term of x only i.e. can be expressed in the term of x and y. e.g.

(i) \[xy=\sin (x+y)\]

(ii) \[\log {{x}^{y}}=2{{x}^{2}}\sin y.\operatorname{cotC}.\]

 

• Constant function : A function f : R\[\to \]R is said to be constant function if \[y=f(x)=C\,\,\forall \,\,x\in R\],

where C = constant,

Domain of f = R

Range of f = | C |

 

 

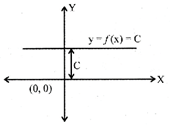
Note: The graph of the constant function is a straight line which is parallel to x - axis.

 

• Identity function: A function f: R\[\to \]R defined as\[y=f(x)=x\], is said to be an identity function.

The domain of f = R

Range at f = R

Here R= Real Number

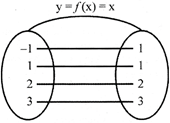
Note: The graph of the identity function is a straight line which is passed through the origin & it is equally inclined to the both the axes.

 

• Exponential function :

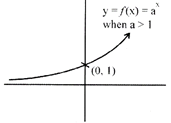
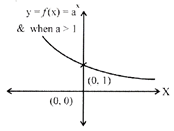
A function f: R\[\to \]R is defined as

\[y=f(x)={{a}^{x}}\], where \[a>0\]& \[a\ne 1\]

is said to be exponential function

The Domain of f = R

Range of \[f=(0,\infty )\to {{R}^{+}}\]

Note: The graph of the exponential function is sketched below.

 

                            

 

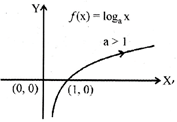
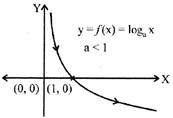
Logarithmic function: A function f: \[(0,\infty )\to R\] defined as \[y=f(x)=lo{{g}_{a}}x,\]\[a\ne 1\,\,\forall \,\,x\in {{R}^{+}}\] is called a logarithmic function.

The domain of\[f=(0,\infty )={{R}^{+}}\]

and range of\[f=(-\infty ,\infty )=R\].

The graph of the function is as shown below.

                                

           

Note: Sometime, \[{{\log }_{e}}x\] is denoted as in\[x\].

• Reciprocal function: A function f: \[R-[0]\to R\] defined as \[y=f(x)=\frac{1}{x}\], is said to be reciprocal function.

The domain of\[f=R-[0]\]

and range of\[f=R-[0]\].

The graph of this function is as shown below:

 

 

• Modulus function or absolute value function:

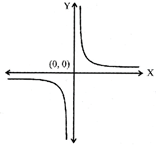
A function \[f=R\to R\] defined as

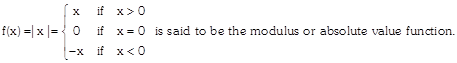
The domain of\[f=(-\infty ,\infty )=R\]

Range of\[f=(0,\infty )\].

The graph of this function is as shown below:

 

 

• Greatest integer or step or integral function.

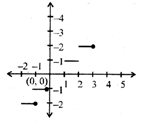
The function\[f:R\to R\] defined as\[f(x)=[x]\] is said to be the greatest integer (step or integral) function.

[x] = integral part of x or greatest integer less than x

Domain of\[f=(-\infty ,\infty )=R\]

Range of f = z = integer number.

The graph of this function is as shown below.

 

 

• Fractional - Part function: The function\[f:R\to R\] defined as\[y=f(x)=x-[x]=\{x\}\], where \[\{x\}=\] fractional part of x, is said to be fractional function - part function.

Domain of\[f=(-\infty ,\infty )=R\]

Range of\[f=[0,1)\].

The graph of this function is as shown below.

 

           

• if x is an integer \[\Rightarrow \] x = [x] then {x}= 0.

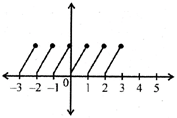
\[\Rightarrow \{[x]\}=0\]

\[\Rightarrow 0<\{x\}<1\]

 

 

• Signum function:

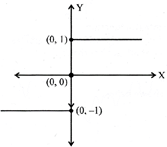
The function\[f:R\to R\] defined as

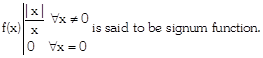
Domain of\[f=(-\infty ,\infty )=R\]

Range of\[f=\{-1,\,\,0,\,\,1\}\].

The graph of signum function can be sketched as shown below:

 

 

• Rational function: A function of the form\[f(x)=\frac{p(x)}{q(x)}\] where \[p(x)\] & \[q(x)\] are the polynomials in the simplest form &\[q(x)\ne 0\], is said to be the rational function.

 

• Trigonometric function:

 

Function	Domain	Range
\[y=\sin x\]	R	\[[-1,\,\,1]\]
\[y=\cos x\]	R	\[[-1,\,\,1]\]
\[y=\tan x\]	\[R-\left( \frac{\pi }{2} \right)\]	R
\[y=\cot x\]	\[R-(\pi )\]	R
\[y=\sec x\]	\[R-\left( \frac{\pi }{2} \right)\]	\[R-(0,\,\,1)\]or\[(-\infty ,-1]\cup [1,\infty )\]
\[y=co\sec x\]	\[R-(\pi )\]	\[(-\infty ,-1]\cup [1,\infty )\]

 

• Inverse Trigonometric function:

 

Function	Domain	Range
\[y={{\sin }^{-1}}x\]	\[-1\le x\le 1\]	\[\left[ \frac{-\pi }{2},\frac{\pi }{2} \right]\]
\[y={{\cos }^{-1}}x\]	\[-1\le x\le 1\]	\[[0,\,\,\pi ]\]
\[y={{\tan }^{-1}}x\]	\[-\infty <x<\infty \]	\[\left[ \frac{-\pi }{2},\frac{\pi }{2} \right]\]
\[y={{\cot }^{-1}}x\]	\[-\infty <x<\infty \]	\[(0,\,\,\pi )\]
\[y={{\sec }^{-1}}x\]	\[R-(-1,\,\,1)\]	\[[0,\,\,\pi ]-\frac{\pi }{2}\]
\[y=co{{\sec }^{-1}}x\]	\[R-(-1,\,\,1)\]	\[\left[ \frac{-\pi }{2},\frac{\pi }{2} \right]-\left\{ \left. 0 \right) \right.\].

 

• Composition of function: Let f and g be two real valued functions defined as f : B\[\to \]C, then the composition of f and g, denoted by g o f, is defined as the function g of: A\[\to \]C is given by (g o f) (x) = g{f(x)} = g (y) \[\forall \,x\in A\] e.g. Let A = {p, q, r, s}, B = {a, b, c, d} and C = {/, m, n}.

Let f: A\[\to \]B and: B\[\to \]C be defined as

f = {(p, a), (q, c), (r, b), (s, a)}

f = {(a, /), (b, /), (c, m), (q, m)}

Then

\[(gof)(p)=g\,(f\,(p))=g\,(a)=/\]

\[(gof)(q)=g\,(f\,(q))=g\,(c)=m\]

\[(gof)(r)=g\,(f\,(r))=g\,(b)=/\]

\[(gof)(s)=g\,(f\,(s))=f\,(a)=/\]

Thus (gof): A\[\to \]C be written as

gof = {(p, /), (r, /), (s, /), (q, m)}.

 

• Inverse function: If function f : A\[\to \]B be both one - one & onto then inverse function\[{{f}^{-1}}\] B\[\to \]A be defined as \[y=f(x)\]\[\Rightarrow {{f}^{-1}}(y)=x\,\,\forall \,\,x\in A\And \forall y\in B.\]

 

• Some results of composition function:

Let f : A\[\to \]B & g : B\[\to \]C be two function

1. If f & g be both one-one then gof will be one-one.
2. If f & g be onto function then (g o f) be onto.
3. If f & g be one-one & onto (i.e. bijective) then go/will be one-one & onto function.
4. If gof be one-onto then f must be one-one but y may or may not be one-one.

 

• Periodic function: A function f (x) is said to be periodic function with period T such that f (x + T)

\[=f(x)\,\,\forall \,\,x\in \,\,\,R\]      ........ (1)

If T is the smallest positive real number, and satisfies the condition\[(1)\], then T is said to be period or fundamental period of f(x).

 

• Tips for checking the periodicity of the function:

(i) First of all put f (x + T) = f (x) to solve the above equation & find the positive value of T.

(ii) If the value of T, independent of x is obtained, then f (x) will be the periodic function with period T otherwise it is non-periodic function.

 

• Some results about periodic functions:

(i) \[\sin x,\] \[\cos x,\]\[\cos ecx,\]\[\sec x\]are periodic functions with period \[2\pi .\]

(ii) \[\tan x,\]\[\cot x\]are also the periodic functions with period \[\pi .\]

(iii) \[|\sin x|,\]\[|\cos x|,\]\[|tanx|,\]\[|\operatorname{cosec}x|,\]\[|\cot x|and|sec\,x|\]are the periodic functions with period \[\pi .\]

(iv) \[{{\sin }^{n}}x,\]\[co{{s}^{n}}x,\]\[\cos e{{c}^{n}}x\And {{\sec }^{n}}x\]are the periodic functions with period \[\pi \] when n is even. Otherwise they are periodic function with period \[2\pi \]when n is odd.

(v) If f(x) is the periodic function with period T, then K f (ax + b) is also a periodic function with period \[\frac{T}{|a|}\] where a, b & \[K\in R\] and a & \[K\ne 0.\]

(vi) If f (x) is the periodic function with period T then \[\sqrt{f(x)}\] and \[\frac{1}{f(x)}\] will be the periodic function with same period T.

(vii) Constant function is a periodic function with no fundamental period.

Solved Examples

1. Find the domain of the function of \[y=f(x)=\frac{1}{\sqrt{{{x}^{2}}-3x+2}}\]

Sol. To define the f (x), we have f (x)>0.

            \[\Rightarrow {{x}^{2}}-3x+2>0\]

\[\Rightarrow {{x}^{2}}-2x-x+2>0\]

\[\Rightarrow (x-2)(x-1)>0\]

\[\Rightarrow x<1\,\,or\,\,x>2\]

So, domain of f = \[(-\infty ,1)\cup (2,\infty ).\]

2. Find the range of \[y=f(x)=\frac{x}{1+{{x}^{2}}}\]

Sol. Obviously.

Domain of f \[=(-\infty ,\infty )=R\]

Now for range

\[\because y=\frac{x}{1+{{x}^{2}}}\]

\[\Rightarrow y.\,\,{{x}^{2}}-x+y=0\]

For x to be real

\[D\ge 0\]

\[\Rightarrow {{b}^{2}}-4ax\ge 0\]

\[\Rightarrow 1-4{{y}^{2}}\ge 0\]

\[\Rightarrow 4{{y}^{2}}-1\le 0\]

\[\Rightarrow (2y+1)(2y-1)\le 0\]

\[\Rightarrow \frac{-1}{2}\le y\le \frac{1}{2},y\ne 0\]

Hence, range of \[y=\left[ \frac{-1}{2},\frac{1}{2} \right]\]