Category : 11th Class
Set Theory
A Set
A set is the collection of things which is well-defined. Here well-defined means that group or collection of things which is defined distinguishable and distinct e.g. Let A is the collection of the group M = {cow, ox, book, pen, man}.
Is this group collection is a set or not? Actually this is not a set. Because it is collection of things but it cannot be defined in a single definition.
For example, A = {1, 2, 3, 4, 5,... n}
Here, collection A is a set because A is group or collection of natural numbers.
e.g. A = {a, e, i, o, u}= {x/x : vowel of English alphabet}
Distinguish Between a Set and a Member
![]()
e.g. A = {2, 5, 8, 7}
\[2\in A\]. It is read as 2 belongs to set A. Or 2 is the member/element of set A.
\[6\notin A\]- It means 6 doesn't belong to set A. A set is represented by capital letter of English/Greek Alphabet.
\[\alpha ,\beta ,\gamma ,\delta \]or A, B, C, U, S etc.
and its all elements is closed with { } bracket.
Hence what is the difference between 2 and {2}
\[\because \]2 can be element of a set whereas {2} represents a set whose one elements is 2.
Note: A set is the collection of distinguish and distinct things
A set can be written/represented in the two form
(a) Tabular form/Roaster form
(b) Set builder form
e.g.
= {\[x/x:\] a vowel of english letter} = It is said to be set-builder form
Note: \[x:x\]or \[x/x\]is read as x such that \[x\]
Type of Sets
(i) Null Set: A set which has no element, is said to be a null set and denoted by \[\phi \,or\,\{\}\]
e.g. (a) a set of three-eyed men
(b) Set of real solution of the equation \[{{x}^{2}}+1=0,\] \[{{x}^{2}}=-1\Rightarrow x=\sqrt{-1}=\]imaginary
(ii) Singleton Set: A set having single element is said to be singleton set.
e.g. A = {2}
(iii) Finite Set: A set having definite and countable elements, is said to be finite set
e.g. \[A=\{a,e,i,o,u\}\]
(iv) Infinite Set: A set having uncountable and indefinite elements is said to be infinite set.
e.g. a set of stars.
(v) Equal set: Two or more than two sets are said to be equal sets if they have the same elements.
e.g. \[A=\{1,\,2,\,5,\,7,\,8\}\], \[B=\{2,\,5,8,1,7\}\]. So, \[A=B\]
e.g. \[A=\{1,\,2,\,3,\,5\}\], \[B=\{2,\,5,7,\,8\}\]
\[A\,\bigcup B=\{1,\,2,3,5,7,8\}\], \[A\,\bigcap \,B=\{2,\,5\}\]
e.g. \[\mathbf{U}=\{1,\,2,3,4,\,5,6,\,7,8,\,9,\,10\}\] Universal set, \[A=\{1,\,4,\,5,\,10\}\], \[B=\{2,\,3,6,\,7\}\]
\[\therefore \,\,A-B=\]difference between A and B\[=\{1,\,4,\,5,\,10\}\], \[\,B-A=\{2,\,3,6,7\}\]
A' = complement of \[A=\bigcup -A=\{2,\,3,\,6,\,7,8\}\], B' \[=\mathbf{U}-B\]
\[=\{1,\,2,3,4,\,5,6,\,7,8,\,9,\,10\}-\{2,\,3,\,6,\,7\}=\{1,\,4,\,5,\,8,\,10\}\]
\[A\,\Delta \,B=\]Symmetric difference between A & B \[=\mathbf{(A-B)}\,\,\mathbf{U}\,\,\mathbf{(B-A)}\]
\[=\{1,\,4,\,5,10\}\,\,\bigcup \,\,\{2,\,3,\,6,\,7\}=\{1,\,2,3,\,4,\,5,6,7,10\}\]
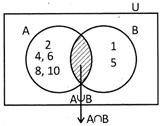
Venn Diagram
\[U=\{1,\,2,3,4,5,6,7,8,9,\,10\}\]
\[A=\{2,\,3,\,4,\,6,7,8,\,10\}\]
\[B=\{1,3,\,5,7,\,\}\]
\[A\,\,\bigcup \,\,B=\{1,\,2,3,4,5,\,6,7,8,10\}\]
\[A\,\,\bigcap \,\,B=\{3,7\}\]
e.g. \[A=\mathbf{\{2,}\,\mathbf{3,}\,\mathbf{5\}}\], \[n(A)=3\]. Total number of subset \[={{2}^{n(A)}}={{2}^{3}}=8\]
e.g. \[A=\{2,\,4,\,5,6\}\],\[B=\{1,\,2,4,\,5,\,6,7,\,8\}\], then \[A\subseteq B\] is true?, \[B\subseteq A\]
\[B\supseteq A\to B\]is a subset of A
\[P(A)=\{\phi ,\,\{2\},\{3\},\{8\},\{2,3\},\{3,8\},\{2,8\},\{2,3,\,8\}\}\]
Mathematically, it is written as
\[A\times B=\{(x,y);\,\,x\in A\,\And Y\in B\}\]
\[(x,y)\to \] Linear ordered pair
e.g. \[A=\text{ }\!\!\{\!\!\text{ 1,}\,\text{2,}\,\text{3 }\!\!\}\!\!\text{ }\], \[\text{B= }\!\!\{\!\!\text{ 2,}\,\text{5 }\!\!\}\!\!\text{ }\]
\[A\times B=\{1,\,2,\,3\}\times \{2,5\}=\{(1,\,2),\,(1,5),(2,\,2),(2,5),(3,\,2),\,(3,5)\}\]
\[B\times A=\{2,5\}\times \{1,\,2,3\}=\{(2,1),(2,2),(2,3),(5,1),(5,\,2),(5,\,3)\}\]worked on
\[(3x+y,x-1)=(x+3,2y-2x)\],
\[3x+y=x+3\Rightarrow 3x-x+y=3\]
\[\Rightarrow 2x+y=3\] ......... (1)
\[x-1=2y-2x\]
\[2y-2x-x=-1\Rightarrow 2y-3x=-1\] ....... (2)
Solving (1) & (2), we have
\[2x+y=3\],\[2y-3x=-1\]
subtracting (2) from (1) x 2, we have
\[4x+2y=6\], \[2y-3x=-1\]
\[7x=7\Rightarrow x=\frac{7}{7}=1\]
Putting the value of x in (1), we have
\[2\times 1+y=3\Rightarrow y=3-2=1\]
\[x=1\], \[y=1\]
\[B=\{2,\,4\}\And C=\{4,\,5\}\]
Find \[(A-B)\times (B-C)\]
Sol: \[{{\mathbf{x}}^{\mathbf{2}}}\mathbf{-5x+6=0}\]
\[\Rightarrow \,\,\,{{x}^{2}}-3x-2x+6=0\]
\[\Rightarrow \,\,\,x(x-3)-2(x-3)=0\]
\[\Rightarrow \,\,\,(x-3)(x-2)=0\]
\[\Rightarrow \,\,\,x-2,3\]
Now, \[A=\{x:{{x}^{2}}-5x+6=0\}=\{2,3\}\]
\[A-B=\{2,\,3\}-\{2,\,4\}=\{3\}\]
\[B-C=\{2,\,4\}-\{4,\,5\}=\{2\}\]
\[(A-B)\times (B-C)=\{3\}\times \{2\}=\{(3,\,2)\}\]
You need to login to perform this action.
You will be redirected in
3 sec
