Category : 11th Class
Complex Number
Complex Numbers: "Complex number is the combination of real and imaginary number".
Definition: A number of the form\[x+iy,\], where \[x,y\in R\] and \[i=\sqrt{-1}\] is called a complex number and (i) is called iota.
A complex number is usually denoted by z and the set of complex number is denoted by C.
\[\Rightarrow C=\{x+iy:x\in R,\,Y\in R,\,i=\sqrt{-1}\}\]
For example: \[5+3i,\] \[-1+i,\] \[0+4i,\] \[4+0i\] etc. are complex numbers.
Note: Integral powers of iota (i)
since \[i=\sqrt{-1}\] hence we have \[{{i}^{2}}=-1,\] and \[{{i}^{4}}=1.\]
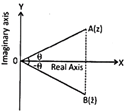
Conjugate of a complex number: If a complex number \[z=a+i\,b,\] \[(a,b)\in R,\] then its conjugate is
defined as \[\overline{z}=a-ib\]
Hence, we have
\[\operatorname{Re}(z)=\frac{z+\overline{z}}{2}\] and \[\operatorname{Im}(z)=\frac{z-\overline{z}}{2i}\]
\[\Rightarrow \] Geometrically, the conjugate of z is the reflection or point image of z in the real axis.
e.g.
(i) \[z=3-4i\]
\[z=3-(-4)=3+4i\]
(ii) \[z=2+5i\]
\[\overline{z}=2-5i\]
(iii) \[\overline{z}=5i\]
\[\overline{z}=-5i\]
e.g. \[{{z}_{1}}=a+ib=(a,b)\]
\[{{z}_{2}}=c+id=(c,d)\]
Then \[{{z}_{1}}+{{z}_{2}}=(a+c,b+d)=(a+c)+i(b+d)\]
\[{{z}_{1}}.{{z}_{2}}=(a,b)(c,d)=(ac-bd,bc+ad)\]
\[{{z}_{1}}-{{z}_{2}}=(a-c,b-d)\Rightarrow {{z}_{1}}-{{z}_{2}}=(a-c,b-a)\]
(a) \[(\overline{z})=z\]
(b) \[z+\overline{z}\] if & only if z is purely real
(c) \[z+-\overline{z}\] iff z is purely imaginary
(d) \[z+\overline{z}=2\operatorname{Re}(z)=2p\] Real part of z
(e) \[z-\overline{z}=2i\,\,lm(z)=2i\] Imaginary part of z
(f) \[\overline{{{z}_{1}}+{{z}_{2}}}={{\overline{z}}_{1}}\pm {{\overline{z}}_{2}}\]
(g) \[\overline{{{z}_{1}}.{{z}_{2}}}={{\overline{z}}_{1}}.{{\overline{z}}_{2}}\]
(h) \[\left( \frac{\overline{{{z}_{1}}}}{{{z}_{2}}} \right)=\overline{\frac{{{z}_{1}}}{{{z}_{2}}}},{{z}_{2}}\ne 0.\]
(i) \[\text{f}i\,\,z=\text{f}({{z}_{1}})\] then \[\overline{z}=\text{f}(\overline{{{z}_{1}}})\]
(j) \[(\overline{{{z}^{4}}})={{(\overline{z})}^{4}}\]
(k)\[{{z}_{1}}{{\overline{z}}_{2}}+{{\overline{z}}_{1}}{{z}_{2}}=2\operatorname{Re}({{z}_{1}}.{{\overline{z}}_{2}})=2.Re({{z}_{1}}.{{\overline{z}}_{2}})\]
Let z = x + iy. Let the square root of a complex number
\[z=x+iy\] is \[u+iv\]
i.e. \[\sqrt{x+iy}=u+iv\] ......... (1)
squaring both sides we have
\[x+iy={{(u+iv)}^{2}}={{u}^{2}}+{{(iv)}^{2}}+2.u.(iv)\]
\[={{u}^{2}}-{{v}^{2}}+2iuv\]
Equating real & imaginary part, we have
\[x={{u}^{2}}-{{v}^{2}}\] ........ (2)
\[y=2uv\] ........ (3)
Now, \[{{u}^{2}}+{{v}^{2}}=\sqrt{{{({{u}^{2}}+{{v}^{2}})}^{2}}+4{{u}^{2}}{{v}^{2}}}\]
\[=\sqrt{{{x}^{2}}+{{y}^{2}}}\] ........ (4)
Solving (2) & (4), we have
\[2{{u}^{2}}=\sqrt{{{x}^{2}}+{{y}^{2}}+x}\]
\[{{u}^{2}}=\sqrt{\frac{{{x}^{2}}+{{y}^{2}}}{2}}+\frac{x}{2}\]
\[\therefore \,\,\,u=\pm \sqrt{\frac{\sqrt{{{x}^{2}}+{{y}^{2}}}-x}{2}}\]
Similarly, \[v=\pm \sqrt{\frac{\sqrt{{{x}^{2}}+{{y}^{2}}}-x}{2}}\]
From (3), we can determine the sign of xy as, if xy > 0 then x & y will be the same sign.
\[\sqrt{x+iy}=\pm \sqrt{\frac{\sqrt{{{x}^{2}}+{{y}^{2}}}+x}{2}},+i\sqrt{\frac{\sqrt{{{x}^{2}}+{{y}^{2}}}-x}{2}}\]
\[=\pm \left( \sqrt{\frac{\sqrt{{{x}^{2}}+{{y}^{2}}}+x}{2}}-i\sqrt{\frac{\sqrt{{{x}^{2}}+{{y}^{2}}-x}}{2}} \right)\]
In short form it can be written.
i.e. \[xy>0\]
Then square root of \[z=x+iy\] i.e. \[\sqrt{x+iy}=\pm \left( \sqrt{\frac{\left| z \right|+x}{2}}+i\sqrt{\frac{\left| z \right|-x}{2}} \right)\]
e.g. Find the square root of 7+24i
Giveen \[z=\sqrt{x+iy}=\sqrt{7+24i}\]
\[\left| \,z\, \right|=\sqrt{{{7}^{2}}+{{(24)}^{2}}}=\sqrt{625}=25\]
Square root of \[z=7+24i\]
\[=\pm \sqrt{\frac{25+7}{2}}=i\sqrt{\frac{25-7}{2}}=\pm \left( \sqrt{\frac{32}{2}}+\sqrt{\frac{18}{2}} \right)\]
\[=\pm (4+i3)=(4+3)\] or\[-(4+3i)\]
Let us consider 0 as origin & OX as x-axis & OY as Y-axis.
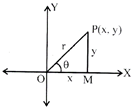
Let \[z=x+iy\] is a complex no. It is represented as \[P(x,y).\]
We draw \[PM\bot OX\] joining P to O (origin)
Then line OP makes positive angle q with X-axis. Then by right angled triangle PMO
\[\cos \theta =\frac{x}{r}=\frac{b}{h}\]
\[\therefore Op=r(say)\]
\[x=r\,\,\cos \theta \] (i)
Similarly,
\[y=r\sin \theta \] (ii)
\[\Rightarrow \]squaring & adding (i) & (ii), we have
\[{{r}^{2}}({{\cos }^{2}}\theta +{{\sin }^{2}}\theta )={{x}^{2}}+{{y}^{2}}\]
\[\Rightarrow {{r}^{2}}={{x}^{2}}+{{y}^{2}}\]
\[r=\sqrt{{{x}^{2}}+{{y}^{2}}}\] &
Dividing (ii) by (i), we have
\[\frac{r\sin \theta}{r\cos \theta} =\frac{y}{x}\,\,\,\,\Rightarrow \,\,\,\,\,\,\tan \theta =\left| \frac{y}{x} \right|\]
\[\theta ={{\tan }^{-1}}\left| \frac{y}{x} \right|\]
Here, z ran be written as
\[z=x+iy=r\cos \theta +ir\sin \theta =r(\cos \theta +\sin \theta )\]
which is said to be polar form of z.
\[z\equiv P(r,\theta )\]
Where
r = radius vector
It is said to be modulus of complex number &
\[\theta ={{\tan }^{-1}}\left| \frac{y}{x} \right|\] is said to argument or amplitude of z.
In exponential form z can be written as \[r{{e}^{i\,\,\theta }}\]
\[\because \]complex number
\[z=x+iy=r(\cos \theta +\sin \theta )=r.{{e}^{i\,\,\theta }}\] (By Euler Method)
e principal value of the argument of z. then \[-\pi <\theta <\pi .\]
Properties of argument of complex number:
Let \[z={{(1)}^{\frac{1}{3}}}\]
\[\Rightarrow {{z}^{3}}=1\]
\[\Rightarrow {{z}^{3}}-1=0\]
\[\Rightarrow (z-1)({{z}^{2}}+z+1)=0\]
If \[z-1=0\Rightarrow z=1\]
If \[{{z}^{2}}+z+1=0\]
Then \[z=-b\pm \frac{\sqrt{{{b}^{2}}-4ac}}{2a}\]
\[=\frac{-1\pm \sqrt{{{1}^{2}}-4.1.1}}{2.1}=\frac{-1\pm \sqrt{-3}}{2}\]
\[z=\frac{-1+\sqrt{3i}}{2},\frac{-1-\sqrt{3i}}{2}\] \[\left[ Q\sqrt{-1}=i \right]\]
Putting \[w=\frac{-1+\sqrt{3i}}{2}\] and \[w=\frac{-1-\sqrt{3i}}{2}\]
Hence, the cube root of the unity be 1,,
(a) Sum of cube roots of unity is zero i.e. \[1+w+w=0\]
(b) Product of imaginary roots is i.e. \[w.{{w}^{2}}=1\Rightarrow {{w}^{2}}=1\]
(c) \[{{w}^{3n}}=1\] \[n\in l\]
(d) \[{{w}^{3n+1}}=w\] & \[{{w}^{3n+2}}={{w}^{2}}\]
(e) \[\overline{\omega }={{w}^{2}},\] & \[{{(\overline{\omega })}^{2}}=w\]
\[(\overline{\omega })w={{w}^{2}},w={{e}^{\frac{2\pi i}{3}}}\]
Similarly, \[{{w}^{2}}={{e}^{\frac{2\pi i}{3}}}\]
The modulus of a complex no. \[z=x+iy\] is written as mod(z) or \[\left| \,z\, \right|=\sqrt{{{x}^{2}}+{{y}^{2}}}\]
It is also said to be the absolute value of z.
e.g. \[z=3+4i\]
\[\Rightarrow \left| \,z\, \right|=\sqrt{{{(3)}^{2}}+{{(4)}^{2}}}=\sqrt{9+16}=\sqrt{25}=5\]
Properties of modulus
(a) \[\left| \,z\, \right|=\left| \,\overline{z}\, \right|\]
(b) \[\left| \,z\overline{z\,} \right|={{\left| \,z\, \right|}^{2}}\]
(c) \[\left| \,{{z}^{4}}\, \right|={{\left| \,z\, \right|}^{4}}\]
(d) \[\left| \,{{z}_{1}}{{z}_{2}}\, \right|=\left| \,z{{\,}_{1}} \right|\,\,\left| \,{{z}_{2}}\, \right|\]
(e) \[\left| \frac{{{z}_{1}}}{{{z}_{2}}} \right|=\left| \frac{{{z}_{1}}}{{{z}_{2}}} \right|,\,{{z}_{2}}\ne 0\]
(f) \[\left| \,{{z}_{1}}+{{z}_{2}} \right|\le \left| \,{{z}_{1}}\, \right|+\left| \,{{z}_{2}}\, \right|\]
(g) \[\left| \,{{z}_{1}}-{{z}_{2}} \right|\ge \left| \,{{z}_{1}}\, \right|-\left| \,{{z}_{2}}\, \right|\]
(h) \[{{\left| \,{{z}_{1}}+{{z}_{2}} \right|}^{2}}+{{\left| \,{{z}_{1}}\,-{{z}_{2}}\, \right|}^{2}}=1\left( {{\left| {{z}_{1}} \right|}^{2}}+{{\left| {{z}_{2}} \right|}^{2}} \right)\]
(i) \[{{\left| \,{{z}_{1}}+{{z}_{2}} \right|}^{2}}={{\left| {{z}_{1}} \right|}^{2}}+{{\left| {{z}_{2}} \right|}^{2}}+2.\operatorname{Re}({{z}_{1}}.{{\overline{z}}_{2}})\]
(j) \[{{\left| \,{{z}_{1}}-{{z}_{2}} \right|}^{2}}={{\left| {{z}_{1}} \right|}^{2}}+{{\left| {{z}_{2}} \right|}^{2}}-2.\operatorname{Re}({{z}_{1}}.{{\overline{z}}_{2}})\]
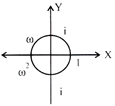
The cube roots of unity lies on the unity circle & divided the circumference of the circle into three equal parts.
If \[z=x+iy=r(\cos \theta +i\,\,\sin \theta )\] & n is a positive integer.
\[\frac{1}{{{z}^{4}}}{{=}^{\frac{1}{{{r}^{n}}}}}{{\left\{ \cos (2\text{K}\pi +\theta )+isin(2\text{K}\pi +\theta ) \right\}}^{\frac{1}{4}}}{{=}^{\frac{1}{{{r}^{n}}}}}\left( \cos \frac{2\text{K}\pi \text{+}\theta }{n}+i\sin \frac{2\text{K}\pi \text{+}\theta }{n} \right)\]
where K = 0, 1, 2, ……(n - 1) e.g. find nth root of unity
\[\because \,\,\frac{1}{{{1}^{n}}}={{(\cos 0{}^\circ +i\sin 0{}^\circ )}^{\frac{1}{n}}}\]
\[=\left\{ \begin{matrix}
\cos (2\text{K}\pi \text{+0)} \\
+i\,\,\sin (2\text{K}\pi +0) \\
\end{matrix} \right\}=\cos \frac{2\text{K}\pi }{n}+i\,\sin \frac{2\text{K}\pi }{n}\]
\[=ei\frac{2\text{K}\pi }{n}\] where, K = 0, 1, 2, 3, 4, ....n.
Putting K = 0, 1, 2, 3, 4....\[(n-1).\]One by one we obtain
\[\frac{1}{{{1}^{n}}}=1,\,e\frac{i2\pi }{n}\,\,,e\frac{4\pi i}{n}\,\,...e\frac{i2(n-1)\pi }{n}=1,\,a,\,{{a}^{2}},{{a}^{3}}.....{{a}^{n-1}}\] where \[a={{e}^{\frac{i2\pi }{n}}}\]
(a) \[1+a+{{a}^{2}}+....{{a}^{n-1}}=0\]
(b) \[1.\,\,a.\,\,{{a}^{2}}.....{{a}^{n-1}}={{(-1)}^{n-1}}\]
\[\log (a+ib)=\frac{1}{2}\log ({{\alpha }^{2}}+{{\beta }^{2}})+i{{\tan }^{-1}}\left( \frac{\beta }{\alpha } \right)\]
\[\log (ib)=\log b+\frac{i\pi }{2}\]
You need to login to perform this action.
You will be redirected in
3 sec
